1. Introduction

This paper is an extension of the work presented at the annual computing SAI conference, London, July 2017 [1]. The strengthening of cryptographic protocols with random numbers [2-4] is widely accepted as mandatory to secure networks of cyber physical systems (CPS). Both pseudo random numbers generators (PRNG) that use mathematical methods [5-8] and true random numbers generators (TRNG) that exploit physical elements [9-11] are mainstream. The randomness based on mathematical algorithms for PRNGs could be weak when crypto-analysts armed with powerful computers know the algorithms. Such algorithms can also consume too much computing power, which may be a problem for small internet of things (IoT) peripherals. The need to quantify the randomness of PRNG, and TRNG is of prime importance [12-15]. Physical Unclonable functions (PUF) can be valuable sources of natural randomness [16-17], they have been adopted for the design of true random number generators (TRNG). However, the randomness of the physical elements is not always acceptable when subjected to temperature changes, aging, electromagnetic interferences, and other parametric drifts. The PUFs can be too predictable in some circumstances, which is not necessarily conducive to the design of quality TRNGs that rely on physical randomness to generate a fresh random number at every query.

      We are presenting how ternary PUFs contain fuzzy elements that are excellent sources of randomness. The method is based on the identification of the cells of memory based PUFs that are naturally unstable under repetitive queries. When tested, the fuzzy cells can switch back and forth randomly between “1” and ”0”, thereby generating random data streams. We are presenting three complementary elements:

1. how a XOR data compiler, which process the data available from multiple ternary cells, can create an extremely high level of randomness [18-21];
2. how a probabilistic model allows the quantification of the level of randomness of the TRNG;

• how the method can be extended to the generation of native ternary random numbers with modulo-3 addition.

2. Designing a random number generator

2.1.  Ternary physical unclonable functions

      There is a growing interest in securing CPS’s with Physically Unclonable Functions (PUFs) to strengthen security when deployed in the cryptographic processes using a powerful set of physically derived cryptographic primitives [22-26]. PUFs act as virtual fingerprints for the hardware during the authentication processes to effectively block cyber thefts, Trojans, and malwares [27-34]. With error correcting methods, the PUFs can also generate cryptographic keys for symmetrical encryption schemes [35-36]. The inherent randomness, unclonability, secrecy, and physical nature of most PUFs makes it extremely hard to inspect during side channel attacks, or when lost to the enemy.

2.2.  Quality considerations for PUFs

      The PUFs, regardless of their design, must exhibit enough predictability overtime for reliable authentications, or encryption. The reference patterns of the PUFs that are generated up front during the setup of protocol, called challenges, are compared over the life of the component with freshly generated patterns, called responses, during the authentication cycles. Quality PUFs need low challenge-response-pair (CRP) error rates, the intra-PUF challenge-response Hamming distance must be small enough to insure small level of false rejection rates (FRR). The PUF challenges should act as predictable “digital fingerprints” of the component, while the responses should be easily recognizable as a measurement of the same “digital fingerprints”. Error rates in the 3-7% range are usually acceptable when combined with error correcting techniques [35-36]. PUFs exploit the device-to-device randomness that is created during the manufacturing process of micro-components; it is desirable that the average inter-PUF hamming distance between different PUFs, divided by the length of the PUFs, should be in the 50% range to insure low level of false acceptance rates (FAR). This is achievable when the level of intra-PUF randomness, also called entropy, is high enough. PUFs with longer streams of bits have therefore higher entropy, and lower FAR. 128-bit CRPs, or higher, are usually required for this purpose.

      Another important figure of merit for PUFs is the number of available CRP configurations for a unit. Strong PUFs, as opposed to weak PUFs, contains large quantities of possible CRPs that are addressable. For example, a ring oscillator PUF with 128 rings is a strong PUF. The number of possible pairing of two rings is N =  = 16,256. If the protocol use 128-bit long CRPs, the number of possible challenges of 2¹²⁸, offers satisfactory entropy, and a low collision rate of the pairs. A memory PUF with random addressing capabilities is even stronger [36, 39-40]. For example, when the capacity of the memory is in the mega-byte range, millions of configurations are providing an entropy much higher than a 128-ring oscillator with “only” 16,256 possible configurations. Existing PUFs can have limitations, and lack of trustworthiness that could create a false sense of security. The signatures of PUFs are derived from intrinsic manufacturing variations, which could become predictable due fabrication excursions. Properties such as critical dimensions of printed structures, doping levels of semiconducting layers, and threshold voltages should make each device unique and identifiable from all other devices, abnormal operations during the manufacturing process could alter such randomness. When subject to changes related to temperature, voltage, EMI, aging, and other environmental factors these parameters can drift over time, the undesirable result, is weak PUFs with CRP error rates as high of 20%.

      The main objective in designing ternary PUFs is to resolve some of these issues, and to reduce the CRP error rates by eliminating fuzzy CRPs during challenge generation. The figure of merit is to achieve trustworthy and robust intra-PUF CRP matching rates with low FRR during authentications, without increasing FAR during inter-PUF authentication of malicious challenges. The by-product of such design is the design of highly random TRNG with the fuzzy cells.

2.3.  Memory based PUFs

      The methods to design PUFs and TRNGs with SRAM memories have been published SRAM [36-38]. SRAM based PUFs have been successfully commercialized. When powered up, each SRAM cells naturally flip to store either a 0, or a 1. In most of the cases, arrays of SRAM cells return to a similar pattern characteristic, i.e. a similar finger print. SRAM based PUFs designed with this feature can be reliable, however heavy error correcting methods are usually needed. The SRAM based PUFs are not particularly immune to side channel attacks. Significant research efforts have been published regarding the design of PUFs with Flash RAMs [39-40], DRAMs [41-44], magnetic RAMs [45-46], and resistive RAMs [47-49]]. The cryptographic protocols leveraging memory PUFs are in general distinct from the ones developed with other mainstream PUFs such as ring oscillators, or gate delay arbiters. As shown in Fig. 1, the value of a parameter P is measured on each cell, and is compared with a threshold. The cells with parameter P below the threshold are “0”s, and are “1”s above the threshold. Examples of parameter P selected to design memory PUFs include: threshold voltages of Flash cells after fixed time programming; charges left on DRAM cells without refresh; high resistance value of MRAM cells after programming; and Vset of ReRAM cells.

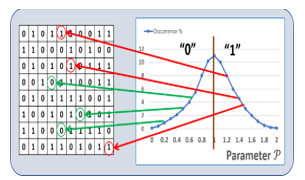Figure 1: Diagram explaining the design of memory based PUF with a parameter P, and a threshold to sort out the states 0 and 1.

The CRP matching is done after error correction. The cell-to-cell physical parameter variations due to manufacturing variations are too erratic for CRP generation. Fig.2 is a diagram showing how a drift of P toward the higher value is forcing the responses of the cells located close to the threshold to switch from 0 to 1, which increase CRP error rates. The cells located far from the transition are not impacted.

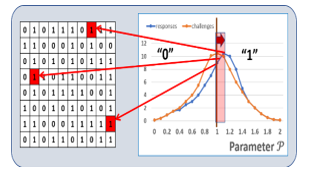Figure 2: Diagram explaining the impact of a drift of parameter P toward higher values, creating CRP errors.

2.4.  Ternary PUFs

      The concept of memory based PUFs with ternary states having random number generation capabilities is described [49-52]. The measurement of P of the cells of a memory PUF allows the segmentation of the cell population into three states. The cells with P <T₁ (a low threshold) carry the state “-“, the cells with P >T₂ (a high threshold) carry the state “+“, and the remaining cells carry the ternary state “0” cells, see Fig.3.

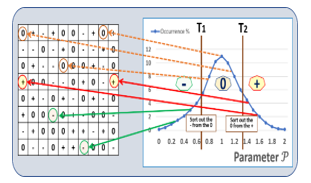Figure 3: Diagram describing the sorting of the memory PUF into ternary states based on parameter P.

During challenge generation, the cells are sorted into ternary states. During response generation, only the cells with “-“ or “+” states are queried, while the cells with “0” state are ignored, see Fig.4. The PUF CRP error rates are significantly lowered, the distance T₂-T₁ acts as a buffer between the states “-“, and “+”.  When the distance T₂-T₁ between thresholds increases, the CRP error rate can reach extremely low values, and is less sensitive to various drifts.

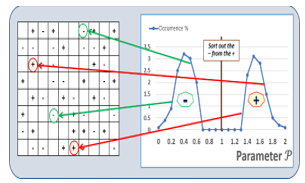Figure 4: Diagram showing the response generation. The “0” states are ignored, only the cells with “-“ and “+” challenges are considered

3. Random number generators

3.1.  Pseudo Random number generators

There are numerous excellent PRNG available to the system developers, which are highly reliable [4-8]. For example, a PRNG {a₁, a₂, …, a_n} can be designed with congruential generators, where a is the multiplier, c the increment, m the modulus, and X_i , b, c, m are natural numbers, typically, c and m are chosen to be relatively prime:

   a_i+1 = (b a_i + c) mod m                 (1)

      Other example of PRNG can constructed by using iterative encryption, as shown in Fig 5, a_i+1 is the cipher of Xi which is encrypted by the code E, and the key K_i . Proving that a PRNG or a TRNG is “random” is a very complicated task that could take years to validate, and billions of data points. The National Institute of Standard and Technology (NIST) has developed an excellent suite of tools available on line that can test the randomness of any random numbers generators [12-15].

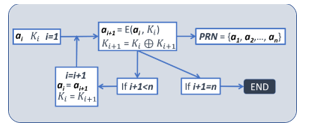Figure 5: Generating the random number PRN from two numbers a_i K_i, and the encryption scheme E.

Examples of parameters that are tested include deviation from randomness, a frequency test (monobit test), Serial test (two-bit test), a Poker test (non-overlapping parts), run tests (gap and blocks), and autocorrelation tests [Menezes, van Oorschot, Vanstone – Handbook of Applied Cryptography].

      In this paper, we are using statistical analysis to quantify randomness, and the parameter λ defined below in this section.  Each bit “a_i” of a data stream of n bits should have a 50% probability to be either a “1” or a “0”. The average deviation from perfect randomness λ is given by:

P₍ a_{i =1)}   = P₍a_{i  =0)} = 0.5                          (2)

                λ   = | 0.5 – P₍ a_{i  =1)} | = | 0.5 – P₍ a_{i =0)} |             (3)

      Assuming that the length of the data stream is n =128, with P₍ a_{i  =0)} = 0.5, the number of possible combinations, also called entropy, is 2¹²⁸= 3.4 10³⁸, which is large enough to protect cryptographic functions from existing or foreseeable computers. When the RNG is not totally random, in this case λ≠0, the entropy is lower than 2¹²⁸, and is further reduced with larger λ. A position paper from (NIST) [12], suggested in 1999 that λ greater than 10^-3 would not be acceptable, sophisticated crypto-analysis methods could be effective to break the PRNG. NIST in 2010 and others [33-34] revisited this. The value of λ that is acceptable to get a safe TRNG is a moving target as modern computers get increasingly powerful. To the best of our knowledge, λ<10^-5 is currently considered an excellent target, while λ<10^-10 is considered outstanding.

3.2.  Use of XOR to enhance PRNGs

Exclusive OR, XOR, is a Boolean logic gate widely adopted in cryptography [18-21]. Two input bits a_i and a_i+1 are transformed into c_i = a_i ⊕ a_i+1, with the following equations:

c_i =0 if a_i = a_i+1 (0⊕0 or 1⊕1)                   (4)

c_i =1 if a_i ≠ a_i+1 (0⊕1 or 0⊕1)                   (5)

      XOR logic is part of most encryption algorithms such as the Data Encryption System (DES), the Advanced Encryption System (AES), and hash functions such as SHA. XOR functions are adding confusion and randomization in the encryption process while been reversible in the decryption process. As part of the encryption, the data streams generated by plain texts are often XORed with cryptographic keys, or sub-keys, then XORed again during decryption. XOR scramblers can enhance randomization in multicarrier communications [19]. XOR are also used to generate scrambling sequences to achieve data randomization in a memory circuit, as well as enhancing random number generators [20]. Some of the important reasons for the use of XOR functions in cryptography are:

• c_i is not disclosing the value of a_i and a_i+1:

c_i =0 can be the result of the pair 00, or the pair 11;

c_i =1 can be the result of the pair 01, or the pair 10;

• XOR is a symmetrical function when applied twice:

                                a_i ⊕ a_i+1⊕ a_i+1 = a_i                          (6)

• If two bits a_i and a_i+1 are random, the bit c_i, defined by c_i =a_i ⊕ a_i+1, is even more random than a_i or a_i+1 .

These properties are exploited in the design of the XOR data compiler as presented in section 4.

3.3.  Ternary PUFs as sources of randomness

The cells of a ternary PUF with “0” state, as described in section 2.3, are exploited as sources of randomness to design TRNG [1, 17], as explained in Figure 6. The cells located in the center of the distribution, the “0” states, can flip back and forward when the value of their parameter P is compared to a threshold centered in the median point of the distribution.

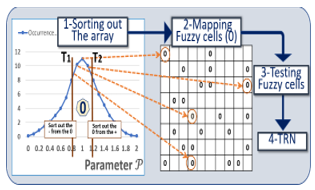Figure 6: Diagram showing how the cells with “0” states

 can be sources of randomness

When the distance T₂-T₁ between the two thresholds used to select the cells with “0” states is reduced, the probability to test these cells either as below the median, or above the median at each query is closer to 50%. For example, the selection of 1,000 cells located close to the median will represents a strong pool to design TRNG. These 1,000 cells can be queried many times to generate long random numbers. Each cell acts as a single source of independant randomness subject to noise, and measurement uncertainties. Within the cells of a particular memory array, the distribution of the physical parameter ?, which determine if a cell is a “0” or a “1”, is following a distribution with a standard variation σ_Array due to cell-to-cell variations created during manufacturing, and other instabilities. Repetitive measurements of parameter ? on the same cell follow a distribution with the standard variation σ_Cell responding to various measurement instabilities, noise, and environmental variations. Low error rate PUFs, with predictable CRPs, should have these variations verifying:

σ_Cell ⪡ σ_Array                               (7)

      When the variations within cells are much lower than the cell-to-cell variations, the “finger print” of the memory PUF is stable and predictable. On the opposite side, to design a TRNG, it is desirable to select only the cells extremely close to the transition of parameter ? between “0’ and “1”, i.e. the one with ternary state “0”. If T_M is the median of the distribution, the average value Tx of ? of each -cells should be such that:

 |Tx – T_M | ⪡ σ_Cell                              (8)

      This maximizes the chance of a random number to flip between “0s” and “1s”. In order to enhance the level of randomness only a very small percentage of the memory arrays are selected as sources of randomness. Current secure micro-controllers have very large embedded memory density, typically in the 1 to 100 Mbits, the percentage of the array consumed for TRNG can be relatively small. In the following sections, we are developing a statistical model to study how to enhance the randomness of a data stream generated from the fuzzy cells. One of the tradeoffs to model is the compromise between tightly selecting the “0” cells around the median T_M, versus improving randomness; in the case of the generation of native ternary streams, we study the use of modulo3 adders.

4. Modeling a ternary PUF for TRNG

      As shown in Fig 7, the cells that are sorted as unstable with a “0” state can be segmented into two subgroups:

• The cells that have a higher probability to be tested above the median are called A-cells, see Fig 8. They have an higher average probability P_A to generate a “1”in the stream of random numbers, their average deviation to randomness is λ_A. The A cells have an average probability P’_A to generate a “0” in the stream of random number:

 P_A= 0.5+ λ_A                               (9)

P’_A= 0.5- λ_A;       1= P’_A + P_A                (10)

• The cells that have a higher probability to be tested below the median are called B-cells, see Fig 9. They have an average probability P’_B to generate a “0”, and an average deviation to randomness λ_B. The average probability P_B to be generate a “1”is:

 P’_B= 0.5+ λ_B                               (11)

P_B= 0.5- λ_B;         1= P’_B +  P_B                (12)

The selection of the transition T_M of parameter ? can be such that the number of A-cells equal the number of B-cells and:

 P_A= P’_B ,     P’_A= P_B ,    λ_A= λ_B.                    (13)

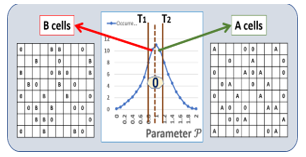Figure 7: The “0” states are segmented into the A cells that more often measured above the median, and the B cells below the median.

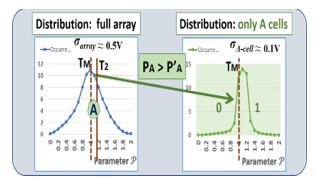Figure. 8: A-cells with higher probability P_A to generate a 1.

Figure. 9: B-cells with higher probability P’_B to generate a 0.

5. A XOR data compiler for TRNG

      As presented below in the experimental section, with 2% of the cell population selected as fuzzy 0-cell, λ_A= λ_B ≈ 2 10^-2 , which is far from the level of randomness needed to generate quality TRNG, this based on NIST criteria. In this section, a XOR compiler is developed, with the objective to enhance the level of randomness of the resulting streams, see Fig.10.

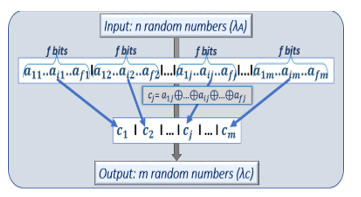Figure. 10: Description of the effect of the XOR operations

      The XOR compiler transforms the incoming streams a_i , i ∈ {1 to n}, generated by the memory PUF by out coming streams c_j,  j ∈ {1 to m}, m<n, of higher level of randomness. The stream of n random numbers generated from the ternary memory PUF is shown below.

Incoming stream:               {a₁, a₂, …, a_i, …a_n}          (14)

This stream is grouped in chunks of f bits, i ∈ {1 to f } ; f < n.

Chunk of bits:                 {a_1j, a_2j, …, a_ij, …, a_fj}          (15)

For example, 1,280 random bits are grouped in 128 chunks of 10 bits. With a XOR, the stream c_j , with j ∈ {1 to m} and n=m.f ,  is generated from the stream a_i , as shown in Fig 10.

Out coming stream:         {c₁, c₂, …, c_j, …, c_m}            (16)

       c_j=a_1j⊕a_2j⊕…⊕a_ij⊕…⊕a_fj     (17)

Such a XOR compiler can be implemented in hardware with only a few logic gates which can be inserted as part of the crypto-processor of the secure processor.  The PRNGs presented section 3.1, are generated sequentially, the random number a_i+1 of a stream of n bits is generated from the previous random numbers a_i . Conversely, the TRNGs with XOR gates can be generated in parallel eq (17) in one cycle. XOR gate is also an addition modulo 2 without carry over. A quicker way to compute eq (17) is to count how many “1s” are presents in the stream {a_1j, a_2j , .., a_fj}. If the number of “1s” in the stream is odd then c_j =1, when even c_j=0.

c_j = a_1j⊕ a_2j⊕ …⊕ a_fj = (a_1j+ a_2j+ … + a_fj ) mod 2     (18)

6. Modeling a 2-bit XOR compiler

We analyze a 2-bit XOR compiler, the incoming data stream of 2n bits is “XORed” two bits by two bits to generate a stream of n bits, f=2. There are three possible configurations for each “XORing”: both cells are A-cells, one cell is an A-cell and the second is a B-cell, and both cells are B-cells. Let us choose: P_A=P’_B=0.52; P’_A=P_B=0.48; λ_B=λ_A=2 10^-2.

• Number of A-cells is even: two A-cells, or two B-cells

          The probability P’_C to have c_j=a_1j⊕a_2j at “0” is occurring when the two cells (a_1j, a_2j) are at (00) or (11):

     P’_C =  = 0.5008 è λ_C =8 10^-4                  (19)

The probability P_C to have c_j=a_1j⊕a_2j at “1” is occurring when the two cells (a_1j, a_2j) are at (01) or (10):

                      P_C =2 (P_A P’_A) = 0.4992                          (20)

• Number of A-cells is odd: one A-cells, and one B-cell.

The probability P_C to have c_j=a_1j⊕a_2j at “1” is occurring when the two cells (a_1j, a_2j) are at (01) or (10):

      P’_C =  = 0.5008 è λ_C =8 10^-4                 (21)

The probability P’_C to have c_j=a_1j⊕a_2j at “0” is occurring when the two cells (a_1j, a_2j) are at (00) or (11):

                    P_C =2 (P_A P’_A) = 0.4992                            (22)

      Let us assume that the incoming stream with 2n bits is generated from a memory PUF with 50% A-cells and 50% B-cells, and with λ_A=2 10^-2. The 2-bit XOR compiler can statistically generate an out coming stream of n bits having 50% C-cells, and 50% D-cells with λ_C=8 10^-4, see Fig. 11. The C-cells are made of pairs of either AA cells or BB cells, while the D-cells are made of pairs of either AB cells or BA cells. In both cases, f =2 is even. The general equations developed below in section 8, eq. (29) to (39) are applicable. When the number of B-cell is even P_C < P’_C, and are reversed when the number of B-cell is odd P_C > P’_C. The deviation from randomness λ_C=8 10^-4 is 25 times smaller than the deviation before the 3bit-XOR compilation, λ_A=2 10^-2.

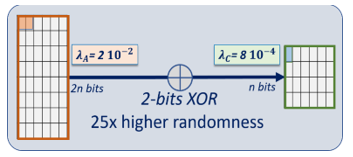Figure. 11: Diagram showing a 2-bit XOR compiler.

7. Modeling a 3-bit XOR compiler

          In this section we analyze a 3-bit XOR compiler, in which the incoming data stream of 3n bits is “XORed” three bits by three bits to generate a stream of n bits, f=3. We are again choosing the same example:

 P_A=P’_B=0.52; P’_A=P_B=0.48; λ_B=λ_A=2 10^-2.

There are four possible configurations for each “XORing”: three cells are A-cells, two cells are A-cells & one cell is B-cell, one cell is A-cell & two cells are B-cells, and finaly three cells are B-cells.

• Number of B-cells is even: three A-cells, A-cell & two B-cells. The probability P_C to have c_j=a_1j⊕a_2j⊕a_3j at “1” is occurring when the three cells (a_1j, a_2j, a_3j) are at (111), (100), (010) or (001):

   P_C =  = 0.500032 è λ_C=3.2 10^-5         (23)

        The probability P’_C to have c_j=a_1j⊕a_2j⊕a_3j at “0” is occurring when the three cells (a_1j, a_2j, a_3j) are at (000), (110), (011) or (101):

              P’_C =  = 0.499968                  (24)

• Number of B-cells is odd: Three B-cells, B-cell & two A-cells. The probability P’_C to have c_j=a_1j⊕a_2j⊕a_3j at “0” is occurring when the three cells (a_1j, a_2j, a_3j) are at (000), (110), (011) or (101):

 P’_C =  = 0.500032 è λ_C=3.2 10^-5       (25)

        The probability P’_C to have c_j=a_1j⊕a_2j⊕a_3j at “0” is occurring when the three cells (a_1j, a_2j, a_3j) are at (000), (110), (011) or (101):

             P_C =  = 0.499968                   (26)

      Let us assume that the incoming stream with 3n bits is generated by a memory PUF having 50% A-cells, and 50% B-cells, and with λ_A=2 10^-2. The 3-bit XOR compiler can statistically generate an out coming stream of 128 bits having 50% C-cells, and 50% D-cells with λ_C=3.2 10^-5, see Fig. 12. The C-cells are made of triplets of either AAA cells, ABB cells BAB cells, or BBA cells. The D-cells are made of triplets of either AAB cells, ABA cells, BAA cells, or BBB cells.

      In both cases, f=3 is odd. The general equations developed in the next section, eq. (29) to (38) are applicable. When the number of B-cells is even, P_C < P’_C, and are reversed when the number of B-cells is odd, P_C > P’_C. The resulting deviation from randomness, λ_c=3.2 10^-5, is 25×25=625 times smaller than the deviation before the 3-XOR compilation, λ_A=2 10^-2.  It is interesting to notice that a 3-bits XOR data compiler needs only 50% more starting cells than a 2-bits compiler, and has a level of non-randomness 25 times lower.

Figure. 12: Diagram showing a 3-bits XOR compiler.

8. Modeling the XOR compiler in general terms

The goal is to develop a model that quantifies the effect of a XOR compiler, which enhance the level of randomization of a data stream, as a function of the size f of the chunk of incoming bits that are XORed together. The incoming stream {a₁, …, a_i, …a_n} has a deviation from randomness λ_A  , and the out coming stream {₁, c₂, …, c_j, …, c_m} has a deviation λ_C. This variation is obtained by computing P_C, the probability for c_j, to be a “1:

 ∣ λ_C ∣ = 1- P_C                                 (27)

The incoming random bits a_ij are generated from A-cells or B-cells of the ternary PUFs. As stated in section 4.1, the transition T_M is selected in such a way that the probability to have an A-cell, and a B-cell is equal to 0.5. If each of the f long chunks have s A-cells and t B-cells with s+t=f.  The numbers of possible combinations (f, s) is:

C_f,s =     = f ! / s ! (f-s) !                      (28):

• All cells of chunk j are A-cells.

       The probability of any of the A-cells of the stream to be a “1” is P_A, and the probability to be a “0”is P’_A. Both P_A and P’_A are following Bernoulli formula:

The terms   of eq. (29) and (30) correspond to a configuration where i bits are “1s”, and f–i bits are “0”.

The probability P_C, is the sum of all terms having i odd:

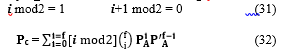
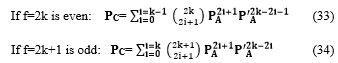The probability P’_C is the sum of all terms having i even:

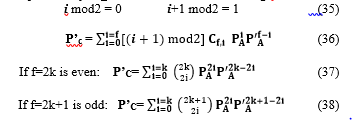When  f is even, P_C < P’_C is written as P_C=0.5-λc_j or P’_C=0.5+λc_j, with λc_j the deviation from randomness of c_j.

When  f is odd, P_C > P’_C and is written as P_C=0.5+λc_j or P’_C=0.5-λc_j.

• Chunks j are a combination of A-cells & B-cells

 The f cells randomly contain A-cells and B-cells. The symmetry between the A-cell and the B-cells (P_A=P’_B and P’_A=P_B) results in the following property:

• If the chunk of bits {a_j1, a_j2, …, a_jf} is generated by an even number of B-cells, the probabilities P_C and P’_C are the same as if the chunk was only generated by A-cells. If f is even, Pc and P’_C are respectively computed with eq. (33) and (37); if f is odd, Pc and P’_C are computed with eq. (34) and (38).
• If the chunk of bits {a_j1, a_j2, …, a_jf} is generated by an odd number of B-cells, the probabilities P_C and P’_C are the opposite of the ones generated by A-cells as described by eq. (37) (33) and eq (38) (34):

 If f is even, Pc is (eq.(37)): P_C= , and P’c is (eq.(34)): P’_C=

If f is odd, Pc is (eq.(38)): P_C= , and P’c is (eq.(35)): P’_C=  

• Simplification of the model

      The objective of this model is to calculate the absolute deviation from perfect randomness, it is not important to know if P_C> P’_C, or if P’_C> P_C. In all cases, lλc_jl is the statistical deviation from pure randomness, regardless of P_C being greater or lower than P’_C. Therefore, assuming that all cells are A-cells is simplifying the computation without reducing the accuracy of the model.

9. Experimental analysis with XOR compiler

9.1.  Variations of ReRAM memory PUFs

The experimental data presented in this paper is based on the study of resistive random-access memory (ReRAM). The cells of ReRAMs, see references [53-60], are constructed with stacks of two electrodes separated by solid electrolytes, the first one is active to REDOX cycles, and the second one is inert. As shown in Figure 13, differential voltages applied on these stacks can move positively, or negatively, elements such as positive oxygen vacancies or positive metallic cations, which result in varying the resistance of the stacks. The basic physical effect described in Fig. 13, can be achieved with several manufacturing technologies:

• Conductive bridge random access memories (CBRAM) that are based on the conduction of cations such as Ag+, or Cu+ through solid chalcogenide electrolytes, or porous silicon [53-58].  The active electrodes could be made of copper, or silver, while the inert electrode can be fabricated with tungsten;
• Memristors devices can operate as ReRAM, or act as active Boolean gates [59-60]. The conductive filaments usually contain oxygen vacancies. The solid electrolyte can be fabricated with HfO, or TaOx.

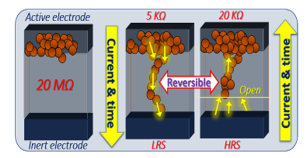Figure. 13: Diagram showing the programming-erase cycles of a ReRAM. After initial forming, the operations are reversible.

In this work, we had access to Cu/TaOx/Pt resistive crossbar arrays fabricated on thermally oxidized Si wafers, Reference [38]. The Cu/TaOx/Pt switches from “0” to “1” based on the formation and the rupture of filaments, made of oxygen vacancies, bridging the dielectric between both electrodes. The initial conditioning of the ReRAM cells, in which conductive filaments are formed, typically requires a positive voltage of approximately 2 to 5 Volt. After forming, the cells can respond to programming and erasing cycles. It exists a minimum negative Vreset voltage applied across the cells, in the -0.5 to -3.0 Volt range, that force the positive ions or oxygen vacancies to migrate back, breaking the conductive filament. The resulting high resistance state (HRS) is then in the 20 Mohm range. In the positive direction, a minimum Vset voltage applied across the switch, reposition the positive ions or oxygen vacancies, forming again the conductive filament. As shown in Fig. 14, when the voltage is ramping, the current remains low until Vset is reached, then the current quickly increases. This effect is reversible, and the filaments can partially be dissolved with opposite voltages.

The parameter ?, that is analyzed for the purpose of designing TRNGs, is the distribution of the Vset across the cells of ReRAM arrays. The entire population of all cells of the array has a Vset distribution that is well represented by a normal distribution having a standard variation σ_Array=0.5V and a median value of 2.1V . The repetitive measurement of the Vset of each cells is also well represented by a normal distribution having a standard distribution σ_Cell= 0.1V.

      For the purpose of random number generation, the Vset of each cell is measured; a cell is considered as a “0” state when Vset<2.1V, and a “1” state when Vset>2.1V. The cells having average Vset measurements at or close to 2.1 Volt, are good candidates for TRNG. The five populations described below are subsets of the total distribution of cells of the array:

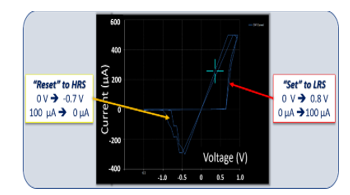Figure. 14: Experimental characterization of the programming-erase cycles of a ReRAM. The cells are responding to positive, and negative voltage ramps, showing Vset, and Vreset.

• Case-1: Only 2% of the cells are the ternary 0-states. They are used to generate the random numbers. For these cells parameter ? is close to the transition of 2.1 Volt. Half of the cells, the A-cells, have P_A=0.52 probabilities to be “1”, P’_A=0.48 probabilities to be “0”, with λ_A=2 10^-2. The second group, the B-cells, have P_B=0.48 probabilities to be “1”, P’_B=0.52 probabilities to be “0”, with λ_B=λ_A=2 10^-2.

P_A=P’_B=0.52; P’_A=P_B=0.48; λ_B=λ_A=2 10^-2        (39)

• Case-2: 4% of the cells are ternary 0-states. The probabilities as defined above are:

P_A=P’_B=0.54; P’_A=P_B=0.46; λ_B=λ_A=4 10^-2     (40)

• Case-3: 7% of the cells are ternary states. The probabilities as defined above are:

P_A=P’_B=0.56; P’_A=P_B=0.44; λ_B=λ_A=6 10^-2      (41)

• Case-4: 11% of the cells are ternary states. The probabilities as defined above are:

P_A=P’_B=0.60; P’_A=P_B=0.40; λ_B=λ_A=1 10^-1      (42)

• Case-5: 100% of the cells are included. The probabilities as defined above are:

P_A=P’_B=0.90; P’_A=P_B=0.10; λ_B=λ_A=4 10^-1     (43)

In this last case, there are no ternary states, the entire memory array is used to generate random numbers.The reason we are considering this range of options is to quantify the effectiveness of the XOR data compiler to generate a random number as a function of how tight the ternary state distribution is. Case-1 is the one with the highest initial randomness, while Case-5 is the lowest one.

9.2.  Effect of the XOR compiler on the TRNG

      The probabilistic model presented in this section is used to analyze the five experimental cases presented above. Fig 15. and Fig. 16 summarize the impact of the XOR data compiler when f varies from 2 to 5. We are observing a lack of efficiency of the XOR compiler in case-5, the one without ternary states. The lack of initial randomness of this case is such that the XORing cannot “clean up” the stream. In other cases, the XOR data compiler when combined with the ternary 0-states is very efficient. Case-1 with the highest level of initial randomness is benefiting the most from the XOR compiler: with 5-cell XOR, λ_C=5.12 10^-8, which is a very small deviation from absolute randomness.

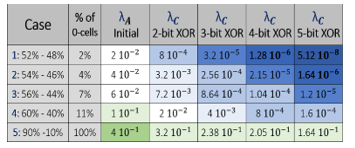Figure 15: Deviation from non-randomness by experimental case

Figure 16: Increased efficiency of the XOR compiler

10. Example of algorithms for TRNG

10.1. Minimization of the impact of parameter drifts

      The randomness of the TRNG originates from the physical parameters of multiple cells that provide independent sources of physical randomness. This is a fundamental strength compared with mathematically generated pseudo RNG (PRNG) because mathematical algorithms cannot describe unclonable physical elements. The cell-to-cell randomness is due to micro-variations during manufacturing and natural noise effect during measurements. However, physical elements can vary often in a predictable way when subject to effects such as temperature change, biasing conditions, and induced attacks. For example, the value of the Vset of a resistive RAM goes down when subject to higher temperature. A hacker could submit the physical element to a hot air blower to increase temperature, reduce Vset, thereby making both A-cells and B-cells appear similar, creating a high probability to be tested as “0”. Such a drift or malicious attack could results in a collapse of the level of randomness with lower entropy. The remedy of such an attack is to make the size of the population of A-cells and B-cells equivalent, by adjusting the threshold (T2) between the “0” states, and “1” states, in the median point of the 0-cell distribution, see Fig 17:

Figure. 17: Algorithm to reduce the effect of a parameter drift.

• Identify n_i cells of the memory PUF that are part of the fuzzy 0-cells; n_i = m_i∗f, in preparation of the f-bit XOR compiler;
• Measure parameter ? of all these ni cells;
• Identification of the threshold T_M placed at the median value of all measurements of parameter ? of the population. By design, half of the cells should have a value below T_M, and half above T_M.
• Generate n_i bits, “0”s below T_M, and “1”s above T_M.
• Use the XOR compiler to combine chunks of f bits together.
• The resulting stream of m_i bits is the stream of the TRNG.

      With this method the raw data stream generated by the memory array and the 0-cell has a population with equal numbers of “0”s and “1”, regardless of a potential drift in temperature caused by a natural variation, or caused by the hot air blower of the hacker. The method is applicable to compensate for any drifts, noise, or aging; the integrity of the TRNG is thereby protected.

10.2. Generalization to other TRNG designs

When the physical component generates a data stream with a deviation from absolute randomness λ_in, it is possible to model the size f of the chunks that are XORed together, as described in Fig.8, to meet a particular λ_out objective. The model can be used as a predictive tool. For example, as shown Fig.18, the number f necessary to compile a data stream of various initial randomness can be anticipated to be λ_C<5 10^-8  or λ_C< 10^-10 . This could be valuable to adjust the compilation as a function of the monitoring of the randomness of the incoming data stream.

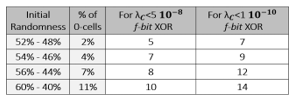Figure 18: Predictive model – f-bit needed for a given objective λ

The proposed method to design TRNG is not limited to ReRAM arrays, and Vset as parameter ?.  The method is applicable to any memory device as long as it is possible to identify a parameter ? that can be reliably tested to sort out the cells and identify enough unstable 0-cells. The algorithm presented Fig. 17 is generic:

• Flash or EEPROM memory: parameter ? can be the trans-conductance of the cells after fixed time programming. The threshold voltage of each cell, after fixed time injection of electrons in the floating gate, vary cell-to-cell due to variations in fabrication parameters such as tunnel oxide thickness and doping levels. Very small changes of threshold voltage can create major changes in the trans-conductance, which are desirable sources of randomness.
• DRAM memory: parameter ? could be the measurement of the residual charge left in a cell after constant discharging time. One effective method is to program all cells, and put the refresh cycle on hold. The fuzzy cells can flip above or below the threshold value of residual charge.
• ReRAM memory: In addition of the Vset as presented in this paper, parameter ? could be the Vreset (threshold voltage to erase the cells), Roff (resistivity on the high resistance state), or Ron (resistivity on the low resistivity state). Some parameters like Roff can be flaky, and jump in a non-erratic way from a set of several discrete values, which is not a desirable source of randomness for a TRNG.
• SRAM memory: the PUFs are based on the determinations of the cells flipping to either a 0 state, or a 1 state after power-off- power-on cycles. However, 3 to 5% of the SRAM cells are fuzzy, they can switch on either states at each cycle. The recommended methodology is to test the SRAM array, and keep track of the 0-states for TRNG.

      The use of the XOR compiler enhances the randomness of any data streams regardless of their origin. The XORing by chunk of f-bits is therefore applicable to a stream of n_i incoming bits, as shown in Fig.19.

• If the length of the incoming stream of n_i bits is not an integer number multiple of f, the two are related by eq(44), ri is the remainder of ni congruent f.

n_i = m_i ∗ f + r_i                            (44)

• Several 0’s can be added to the stream of r_i bits to form a chunk with a length f. The total number of chunks will be equal to m_i + 1.
• The XORing is done by chunks of f
• The resulting stream of m_i + 1 has a deviation to non-randomness that is lower than the incoming stream n_i.

Figure. 19: Generalization of the concept to any data streams.

11. Native ternary random numbers generators

In this section, we are presenting a method to directly generate native random trits from PUF memory arrays, as well as ways to enhance randomness with modulo 3 sum adders. As presented in the first section, the fuzzy cells of the PUFs are used as multiple sources of randomness, and the XOR compilers replace mod3 adders.  Ternary computing uses trits, for example (0, 1, 2) or balanced (-, 0, +), instead of the bits (0, 1) used in binary computing [61-67]. Can ternary computing improve cybersecurity and Information Assurance [68-70]? Ternary computing is not a new concept, and is more complex to implement than binary computing. One suggested architecture uses heterogeneous computing elements, and combine binary units to run legacy codes, and native ternary computing units for security [71]:

• Better handling of the natural fuzziness, with lower reliance on error correction codes;
• Can take advantage of ternary hardware, and advances in microelectronics, such as the ternary PUFs described in the first section of this paper [72-79];
• The cryptography based on ternary states has more entropy, and additional levels of freedom to protect both hardware, and software.

For example, let us assume that the length of a data stream is N=128. The number of possible combinations for binary streams is 2¹²⁸= 3.4 10³⁸, and becomes 3¹²⁸= 1.2 10⁶¹  for ternary streams, which is considerably larger. Native random numbers are valuable for cryptographic protocols based on ternary computing. One way to create ternary random numbers is to convert binary random numbers into decimal numbers, then to convert the decimal data stream back into ternary random numbers. Such a method add complexity, and can potentially expose the random numbers to hackers. A direct generation of native ternary random numbers is therefore desirable. The definition of deviation from perfect randomness for ternary TRNG, is similar to the one developed for binary data streams. As presented in the first section, each bit a_i of the perfectly binary random stream {a₁, …, a_i, …, a_n} should have precisely the same probability to be either a “1” or a “0”. The average deviation from randomness, λ is given by:

 P₍a_{i =1)} = P₍a_{i =0)} = 0.5                        (50)

λ = ½ (|P₍a_i=1) – 0.5| + |P₍a_i=0) – 0|

= |P₍a_i=1) – 0.5| = |P₍a_i=0) – 0.5|                (51)

 In the case of ternary data streams of trits with “-“, “0”, and “+” states,  the term λ is given by:

λ= 1/3(|P ₍a_{i  = –)} – 1/3|+|P ₍a_{i  = 0)} – 1/3|+|P₍a_{i  = +)} – 1/3|)  (52)

0 = P ₍a_{i  =  – )} + P ₍a_{i  = 0 )}  + P₍a_{i  = + )}                 (53)

12. Description of the method

12.1. Segmentation of the fuzzy cells of the memory PUFs

The fuzzy cells , the 0-cells, can be segmented into three subgroups, see Fig. 20:

• The cells that have a higher probability to be tested as “-” are called A-cells. They have an average probability P_{A= –} to be tested as “-” , P_{A= 0} to be tested as “0”, and P_{A= +} to be tested as “+”.
• The cells that have a higher probability to be tested as “0” are called B-cells. They have an average probability P_{B= –} to be tested as “-” , P_{B= 0} to be tested as “0”, and P_{B= +} to be tested as “+”.
• The cells that have a higher probability to be tested as “+” are called C-cells. They have an average probability P_{C= –} to be tested as “-” , P_{C= 0} to be tested as “0”, and P_{C= +} to be tested as “+”.

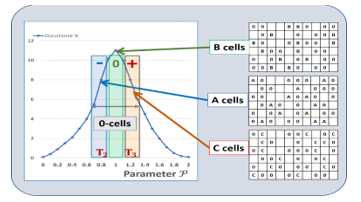Figure 20: segmentation of the fuzzy cells in trits

The selection of the transition of parameter ? between “-” and “0” , T2, and the transition of parameter ? between “0” and “+”, can be such that the total number of A-cells selected within the 0-cells equal the number of B-cells, and the number of C-cells. The deviation from perfect randomness λ of the stream of native ternary random numbers generated from the fuzzy cells A, B, C is given by:

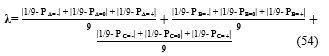12.2.  Enhancement of the randomness with mod3 adders

The algorithm using a mod3 adder, see Fig.21 and 22, is similar to the one presented section A.

• The number of cells needed to generate a stream of mi trits is n_i = m_i∗f , they are selected as part of the fuzzy 0-cells of the ternary memory PUF;
• Parameter ? is measured on all n_i cells;
• The population of ni cells is segmented into three third based on the value of ?. The threshold separating the bottom third and the central third is T₂; the threshold separating the central third and to top third is T₃;
• With the segmentation in three done step 3, the n_i cells at the bottom third are carrying “-“state, the cells in the middle are “0”s, and the cells at the top third are “+”s;
• The stream of trits is added by chunks of f trits; Instead of a XOR compiler, the mod 3 adder of chunk of trits enhance randomness. With mod 3 sum adders, two input trits a_i, and a_i+1 are transformed into c_i = a_i ⊕ a_i+1, with the following truth table:

(a_i =0; a_i+1 = -), or (a_i = -; a_i+1 =0), or (a_i=a_i+1 =+)èc_i =  –

(a_i =+; a_i+1= -), or (a_i = -; a_i+1= +), or (a_i=a_i+1 =0)èc_i = 0

(a_i=0; a_i+1= +), or (a_i= +; a_i+1 =0), or (a_i=a_i+1 = -)èc_i = +

• The resulting m_i trits are more random.

Mod 3 addition increases randomness, the knowledge of c_i is not disclosing the value of a_i and a_i+1.  c_i = –, 0, or + can be the result of three possible pairs {a_i a_i+1}, with equal probability. If two trits a_i and a_i+1 are somewhat random, the trit c_i is even more random than either a_i  or a_i+1. Let us assume that the stream of random trits generated by the 0-cells of the memory PUF array is {a₁, a₂, …, a_i, …a_n}.

Figure 21: Algorithm to reduce the effect of a parameter drift.

Figure 22: description of the mod 3 adder

As it is shown in  Fig.22, this stream is grouped in chunks of f trits {a_1j, a_2j, …, a_ij, …, a_jf} with f < n. For example, 1,280 random bits a grouped in 128 chunks of 10 bits. The resulting stream of random trits obtained with mod 3 sum adders data {c₁, c₂, …, c_j, …, c_m} is defined as follow:

c_i = a_1j⊕ a_2j ⊕ … ⊕ a_ij⊕ …⊕ a_jf mod 3             (55)

Mod 3 sum adders can be implemented at the software level, or in hardware with only a few logic gates. These gates can be inserted in the state machine of the PUF memory to directly feed secure processors, and crypto-processors with streams of randomly generated trits.

13. Modeling of the randomness after mod3 additions

13.1. Model with mod3 addition by chunks of two trits

In this section we are proposing a simplified model that quantifies the level of randomness of mod 3 adders when two adjacent trits are added mod3. Fig.23 shows such a scheme. We are assuming that the 0-cells are distributed into three type of cells (A, B, and C), each of them with a probability of occurrence of 1/3. Statistically the stream of trits {a₁, a₂, …, a_i, …a_n} contain trits with equal probability to be “-“, “0”, or “+”, also with a value of 1/3. However A-cells have a higher probability to have “-“s, B-cells have a higher probability to have “0”s, and C-cells have a higher probability to have “+”s.

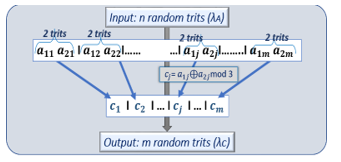Figure 23: description of the mod 3 adder by chunk of two trits

In Fig.24, we are showing an arbitrary set of probabilities verifying that the probability to have either A, B, or C cells is 1/3, and the probability to have either “-“, “0”, or “+” states is also 1/3. In this table:

P_{A= –} = 1/9 + Δ_A- ∗ λ ; with Δ_A1 = 1.8                   (55)

P_{B= 0} = 1/9 + Δ_B0 ∗ λ ; with Δ_A2 = 0.9                  (56)

P_C=+ = 1/9 + Δ_C+ ∗ λ ; with Δ_C+ =1.8                   (57)

Figure 24: example of probabilistic representation

The initial randomness is:

λi = (1/9)( )

= 1/9 (3.6 + 1.8 + 3.6) ∗ λ = λ                   (58)

Other tables and more complicated model can replace this arbitrary representation; however, the suggested simplified model describes quite well the experimental observations. When the cells are combined by pairs, and the trits added mod 3, 9 combinations of cells are possible with an equal probability of 1/9: AA, AB, AC, BA, BB, BC, CA, CB, CC. The average probability to have trits with “-“, “0”, and “+” is 1/3.

 Two cells AA have three possible combinations which can result in a trit at “-“ :

• Both cells at “+”, the probability is: (P_{A= +} ∗ P_{A= +} );
• The first cell is at “0”, the second at “-“ , the probability is: (P_{A= 0} ∗ P_{A= –} );
• The first cell is at “-“, the second at “0”, the probability is: (P_{A= –} ∗ P_{A= 0} ).

The resulting probability P_{AA= –} that two cells AA can result in a trit at “-“ is given by:

P_{AA= –} =(P_{A= +}∗ P_{A= +})+(P_A=0 ∗  P_{A= –})+(P_{A= –}∗  P_A=0 )

=(1/9-1.35∗λ)²+2(1/9+1.8∗λ)(1/9-0.45∗λ)=1/27+0.2∗λ²  (59)

In Fig.25 is showing the result of the computations of 27 configurations: probability to get “-“, “0”, or “1” after addition mod 3 for each pair P_{AA= –}, P_{AA= 0}, P_{AA= +}, P_{AB= –}, P_AB=0,…

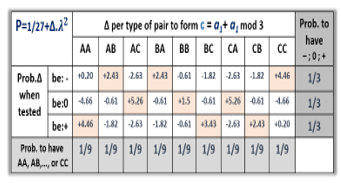Figure 25: probability per configuration after mod 3 addition of two trits.

The resulting deviation from randomness λ’f after addition is the average deviation of these 27 configurations:

λ’f = (1/27)  ≈ 2.27                   (60)

For example, if the initial deviation from randomness for the incoming stream is λ_i = 2 10^-2; the resulting deviation is:

λ’f = 2.27 ∗( 2 ∗ 10^–2)² =  8.7 10^-4               (61)

After addition, the 9 possible configurations shown in Fig.25 can be then combined into 3 types of cells A’, B’, and C. For example, the cells that are mainly “-“, the A’-cells consist of the mod3 additions of CC, AB, and BA pairs. In this case, the average deviation from randomness of A’-cells when they are containing a trit “-“is:

 (λ’f _{A’= –} )= 1/3(( λ’f _{CC= –} ) + (λ’f _{AB= –}) + (λ’f _{BA= –}))

= 1/3 (2.43+2.43+4.46) ∗ = 3.10 ∗                (62)

13.2. Extension of the model with chunks of four trits

The method presented section II 2.2 can be extended to the addition mod3 of 4 sequential trits to generate trits of higher randomness. Rather than starting with the three types of cells A, B, and C having a deviation from randomness λ, the same computation is done with the cells A’, B’, and C’ having a deviation from randomness equal to 2.27 ∗  .

The resulting deviation from randomness λ”f of the new stream of trits and mod 3 addition of chunks of four bits is:

λ”f = 2.27 (λ’f)² = 2.27 (2.27)² ≈ 11.3                (63)

If the initial deviation is λ= 2 10^-2; the resulting deviation is:

λ”f = 11.3 ∗ (2 ∗ 10^–2)⁴ = 1.81 10^-6                 (64)

By extension, after addition of 8 sequential trits, the deviation from randomness λ”” will be:

λ””f = 2.27 (λ”f) ²≈ 290                       (65)

If the initial deviation is λ= 2 10^-2; the resulting deviation is:

λ””f = 290 ∗ (2 ∗ 10^–2)⁸  = 7.4 10^-12                (66)

14. Experimental analysis with mod3 adders

      The analysis is based on the data presented in the first section related to the measurement of the Vset of ReRAM devices. We are again considering the same five cases to sort out the fuzzy “0-cells”:

• Case-1: Only 2% of the cells are 0-cells. For these cells parameter ? is very close to the transition of 2.1 Volt.

λ_i=2 10^-2;

• Case-2: 4% of the cells are 0-cells. λ_i=4 10^-2;
• Case-3: 7% of the cells are 0-cells. λ_i=6 10^-2;
• Case-4: 11% of the cells are 0-cells. λ_i=1 10^-1;

This range of options allows the quantification of the effectiveness of the addition mod 3 to scramble the trits, as a function of the initial randomness coming from the ternary PUF memory. Case-1 is the one with the higher initial randomness, while Case-4 is the lowest one.

The probabilistic model developed above, is the base of the analysis of the four experimental cases. The results of the computations are shown in Fig.26 and Fig. 27.

The impact of the addition modulo 3 addition on the level of randomness on the resulting data streams of trits is increasing when the number of cells f involved in the addition increases from f = 2 to f = 8.

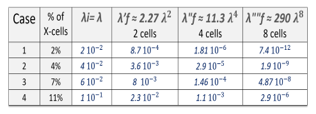Figure 26: modeling of the effect of mod 3 addition as a function of the experimental cases.

In all cases the addition mod 3 when applied to a data stream of trits generated by a PUF is very efficient to enhance randomness. Case 1, the one with the highest level of initial randomness, benefit the most from mod 3 sum adders.

It is interesting to notice that the XOR compiler, and the mod 3 addition have similar effects in improving randomness. The model can be used as a predictive tool to anticipate the level of randomness of streams of trits. For example, as shown in Fig.27, the number cells necessary to get λ<5 10^-6 for case 1 is 4, it is 5 for case 2, it is 6 for case 3, and it is higher than 8 for case 4.

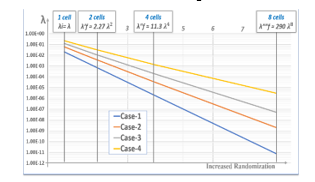Figure 27: deviation from perfect randomness plotted as a function of the size of the chunk of trits involved in mod3 addition for the four cases.

Discussion and conclusion

The use of ternary PUFs to design TRNG, combined with a XOR compiler, or a modulo 3 addition has the following benefits:

• The cells with fuzzy behavior of a ternary PUF, the 0-cells, can provide multiple sources of independent randomness. A memory arrays in the megabyte range can have a large quantity of such cells;
• The randomness of the binary data streams extracted from the ternary 0-cells are enhanced by a XOR compiler. Based on a normal distribution of parameter ?, the proposed statistical model can quantify the deviation from pure randomness of the TRNGs. It is possible to calculate f, the length of the XOR, to reach a desired level of non-randomness λ_f, as a function of the level of non-randomness λ_i of the incoming data stream extracted from the physical element.
• The randomness of the ternary data streams extracted from the 0-cells can be enhanced by a modulo 3 adder. It is the possible to directly generate a stream of random trits without having to convert binary data streams into ternary data streams;
• It is possible to anticipate, with the suggested probabilistic model, the minimum size of chunks of data f that need to be processed to reach the level of randomness λ_f. This is the case for the XOR compiler, and the mod 3 adder;
• The proposed methodology minimizes sensitivity to parameter drifts such as temperature, aging, or biasing conditions. It is anticipated that the drifts should not materially degrade the quality of the TRNGs.
• The hardware implementation of both the XOR compiler, and the mod 3 adder can use known commercial CMOS circuitry.
• The method can reach NIST expectations in term of deviation from pure randomness of the TRNG, even if the randomness created by the PUF is weak.

The experimental section of this work, which is based on the measurements of the Vset of ReRAM cells, produced a distribution that is able to show enough randomness to generate random numbers. We noticed that the XOR data compiler is not effective when the initial data stream is not random. The model developed assumes that the initial random numbers generated from the 0-cells are symmetrically distributed between A-cells and B-cells.

Other statistical distributions beside the normal one are under consideration in our research effort. We are not anticipating that these improved statistical models will significantly change the outcome when only cells close to the median distribution are selected. This is not the case for wider distribution of the 0-cells away from the median.

      Future work: The objective of this work was to develop TRNG for cryptographic protocols that can be embedded in the Internet of Things (IoT). The implementation of affordable sources of randomness to secure IoTs can benefit from the ease of use of ternary PUFs, which are tamper resistant. TRNGs are essentials elements to encryption protocols involving PUF CRPs, and other cryptographic keys. We are studying the design of a prototype that incorporates the proposed TRNG scheme with various ReRAM arrays. The prototype is intended to automatically extract large quantities of PUF CRPs and random streams of bits, and trits. We intend to use the prototype to further validate our statistical models, and to leverage the tools developed by NIST that are available online to quantify the entropy, and the level of randomness of the TRNGs. The prototype should have the built-in flexibility to allow us to analyze multiple types of memory arrays, with different methods of fabrication.

      We are interested in optimizing the randomness of the TRNG while reducing CRP error rates of the PUFs, and developing cryptographic protocols that leverage the combined capabilities. The method described in this paper can be used to the swarm dynamics generating true random noises [8], and other similar applications requiring TRNG. To accelerate the process to generate fresh random numbers on demand, the 0-cells can be tested in advance [80], and the data can be stored in the memory. The read time of a ReRAM is typically 10ns/bit, so we believe that the generation of the TRNG has the potential to be done at a rate of 100Mbit/s. The method presented in this paper can also be extended to n-value logic, for example quaternary logic (4 bits), pentagonal logic (5 bits), or hexagonal logic (6bits). In such cases the 0-cells are divided in n different type of cells, and the addition of chunk of n-bits is done modulo n.

Aknowledgment

Dr. Marius Orlowski from Virginia Tech produced, and characterized the metal oxide ReRAM samples [49]. These measurements were used to prepare the experimental analysis. Dr. Derek Sonderegger from the Department of Mathematics and Statistic of Northern Arizona University provided input for the development of the statistical model. The author is thanking both Dr. Donald Telesca from the US Air Force Research Labs for his support in this work.

1. B. Cambou; A XOR data compiler combined with PUF for TRNG; SAI/IEEE computing conference, July 2017;
2. C. Paar, and J. Pezl; Understanding Cryptography- A text book for students and practitioners; Spinger editions, 2011;
3. C. P. Pfleeger, et al; Security in Computing; Fifth edition; Prentice Hall editions, 2015;
4. R. Soorat; Hardware random number generation for cryptography; https://arxiv.org/pdf/1510.01234 , 2015;
5. D. Glosemeyer, and B Knapp; Random Number Generation; Wolfram Mathematical Tutorial collection, 2008;
6. M. Stipevic, et al; true random number generator; Open problems in Mathematics and computational science; pp.275-315, Springer, 2014;
7. H. Katzgraber; Random Numbers in scientific computing: an introduction; Int. school comp. science, 2010, Oldenburg, Germany
8. Y. Shang, and R. Bouffanais; “Influence of the number of topologically interacting neighbors on swarm dynamics”; Scientific Reports DOI: 10.1038/srep04184, 2015.
9. Berndt Gammel, et al; Jul 2012; Random Generator configured to combine states of memory cells; US patent No 7,979,482 B2;
10. Daniel E Holcomb, et al; Power up SRAM state as an identifying Fingerprint and Source of True Random Numbers; IEEE Trans. On Computers, 2009 Vol 58, issue No09 Sept;
11. Sang-Yong Yoon, et al; Aug 2012; Method of operating nonvolatile memory devices storing randomized data generated by copyback operation; US patent No: 8990481 B2;
12. J. Soto; Statistical testing of random number generators; 1999 – NIST; http://csrc.nist.gov/rng/rng5.html ;
13. A. Rukhin, and all; A statistical Test Suite For Cryptographic Applications; NIST publication 800-22rev1a, April 2010.
14. P. L’Ecuyer; Software for uniform random number generation: distinguishing the good from the bad; 2001 Simulation Conference;
15. A. Rukhin, et all; A statistical test suite for random and PRNG for cryptographic applications; 2010, publication from NIST 800-22 rev 1a;
16. A. Maiti, et al; PUF and TRNG: a compact and scalable implementation; GLSVLSI’09, May 2009, Boston;
17. B. Cambou; Sept, 2015; Random numbers generator with ternary memory; US patent application 2017-0046129;
18. G. Marsaglia; XOR shift RNG; Journal of Statistical software, 2003.
19. M. C Tzannes, A. Friedmann; Nov 2001; Randomization using an XOR scrambler in multicarrier communications; US patent No 9191939 B2;
20. R. Davies; XOR and hardware random number generator; http://www.robertnz.net/pdf/XOR2.pdf; February 2002;
21. B. Cambou; Data compiler for True Random Number Generation and Related Methods; NAU disclosure D2017-03, Aug 2016;
22. Y. Gao, and all; Emerging Physical Unclonable Functions with nanotechnologies; IEEE, DOI: 10.1109/ACCESS.2015.2503432;
23. N. Beckmann, et al; Hardware-based public-key cryptography with public physically unclonable functions; in Information Hiding, New York, NY, USA: Springer-Verlag, 2009, pp. 206–220.
24. Guajardo, J, et al; PUFs and PublicKey Crypto for FPGA IP Protection; Field Programmable Logic and Applications, 2007.
25. David. Naccache and Patrice. Frémanteau; Aug. 1992; Unforgeable identification device, identification device reader and method of identification; Patent US5434917.
26. Guajardo, J., et al; FPGA Intrinsic PUFs and Their Use for IP Protection; CHES, 2007;
27. R. Pappu, B. Recht, J. Taylor, and N. Gershenfield; 20 Sept 2002; Physical one-way functions; Science. Vol 297 No5589 pp2026-2030.
28. Yier Jin; Introduction to hardware security, Electronics 2015, 4, 763-784; doi:10.3390/electronics4040763.
29. R. Maes; Physically Unclonable functions: constructions, properties, and applications; Doctoral thesis- Catholic University of Leuven, 2012;
30. Herder, C., et al; “PUFs and Applications; A Tutorial.” Proceedings of the IEEE 102, no. 8 (2014): 1126-1141;
31. B. Gassend, et al; Silicon PUFs; CCS’ 2002;
32. B. Gassend; Physical random functions; M.S. thesis, Dept. Electr. Eng. Comput. Sci., MA, USA, Massachusetts Inst. Tech.., Cambridge, 2003;
33. S. Katzenbeisser, et al; PUFs: myths, fact or busted? A security evaluation of PUFs cast in silicon; CHES 2012;
34. Christian Krutzik; Jan 2015; Solid state drive Physical Unclonable Function erase verification device and method; US Patent Application publication US 2015/0007337 A1
35. H. Kang, Y. Hori, T. Katashita, M. Hagiwara, and K. Iwamura; Cryptographic Key Generation from PUF Data Using Efficient Fuzzy Extractors; in Proc. ICACT, 2014, pp.23–26.
36. R. Maes, P. Tuyls and I. Verbauwhede, “A Soft Decision Helper Data Algorithm for SRAM PUFs,” in 2009 IEEE International Symposium on Information Theory, 2009.
37. Daniel E. Holcomb, Wayne P. Burleson, Kevin Fu; Nov 2008; Power-up SRAM state as an Identifying Fingerprint and Source of TRN; IEEE Trans. on Comp., vol 57, No 11.
38. D. E. Holcomb, and all; Power-up SRAM state as an Identifying Fingerprint and TRN; IEEE Trans. Comp. Nov 2008;
39. Pravin Prabhu, Ameen Akel, Laura M. Grupp, Wing-Kei S. Yu, G. Edward Suh, Edwin Kan, and Steven Swanson; June 2011; Extracting DeviceFingerprints from Flash Memory by Exploiting Physical Variations; 4th int. conference on Trust and trustworthy computing;
40. V.Zhirnov, et al; Chapter 26: Flash memories; Nanoelectronics and Information Technology; Rainer Waser editor, 2012 Wiley;
41. T. A. Christensen, and all; PUF utilizing EDRAM memory cell capacitance variation; Patent: US 8,300,450B2; Oct, 2012;
42. T. A. Christensen, J. E Sheets II; 2012; Implementing PUF utilizing EDRAM Memory Cell Capacitance Variation; US Patent 8,300,450 B2.
43. K.K. Chang et al; Understanding Reduced-Voltage Operation in Modern DRAM Chips: Characterization, Analysis, and Mechanisms; Cornell Technical Library: 1705.102992, May 2017;
44. U. Schroder, et al; Capacitor-based Random-Access Memories; Nanoelectronics and information technology; Wiley-vch, R. Waser editor, pp 635-654, 2012;
45. Xiaochun Zhu, Steven Millendorf, Xu Guo, David M. Jacobson, Kangho Lee, Seung H. Kang, Matthew M. Nowak, Daha Fazla; March 2015; PUFs based on resistivity of MRAM magnetic tunnel junctions; Patents. US 2015/0071432 A1.
46. Elena I. Vatajelu, Giorgio Di Natale, Mario Barbareschi, Lionel Torres, Marco Indaco, and Paolo Prinetto; July 2015; STT-MRAM-Based PUF Architecture exploiting Magnetic Tunnel Junction Fabrication-Induced Variability; ACM transactions.
47. A. Chen; Comprehensive Assessment of RRAM-based PUF for Hardware Security Applications; IEDM IEEE; 2015;
48. B.Cambou; Enhancing Secure Elements- Technology and Architecture; Springer Int. Publishing Foundations of Hardware IP Protection, 2017;
49. B. Cambou, and M. Orlowski; PUF designed with ReRAM and ternary states; CISR 2016, April 2016, Oak ridge;
50. D. Yamamoto, K. Sakiyama, K. Ohto, and M. Itoh; Uniqueness Enhancement of PUF Responses Based on the Locations of Random Outputting RS Latches; CHES 2011;
51. B. Cambou; PUF generating systems and related methods; US patent disclosure No: 62/204912; Aug 2015;
52. B. Cambou, and F. Afghah; PUF with Multi-states and Machine Learning; CryptArchi 2016
53. Gilbert, Nad, et al. “A 0.6 V 8 pJ/write Non-Volatile CBRAM Macro Embedded in a Body Sensor Node for Ultra Low Energy Applications.” VLSI Circuits (VLSIC), 2013 Symposium on. IEEE, 2013;
54. M. N. Kozicki, M. Park, and M. Mitkova, “Nanoscale memory elements based on solid-state electrolytes,” IEEE Trans. Nanotechnol, vol. 4, pp. 331-338, May 2005;
55. M. N. Kozicki and M. Mitkova, “Mass transport in chalcogenide electrolyte films – materials and applications,” J. of Non-Crystalline Solids, vol. 352, pp. 567-577, March 2006;
56. Valov, R. Waser, J. R. Jameson and M. N. Kozicki, “Electrochemical metallization memories – Fundamentals, applications, prospects,” Nanotechnology, vol. 22, p. 254003, June 2011;
57. M. N. Kozicki, M. Balakrishnan, C. Gopalan, C. Ratnakumar, and M. Mitkova, “Programmable metallization cell memory based on Ag-Ge-S and Cu-Ge-S solid electrolytes,” Proc. NVMTS, p. 8389, 2005;
58. M. N. Kozicki, C. Gopalan, M. Balakrishnan, M. Park and M. Mitkova, “Nonvolatile memory based on solid electrolytes,” in Proc. IEEE Non-Volatile Memory Technol. Symp., 2004;
59. Gargi Ghosh and Marius Orlowski; 2015; Write and Erase Threshold Voltage Interdependence in Resistive Switching Memory Cells; IEEE trans. on Electron Devices, 62(9), pp. 2850-2857.
60. P. R.Mickel, A. J. Lohn, B. J. Choi, J. J. Yang, M. X. Zhang, M. J. Marinella, C. D. James, and R. S. Williams, “A physical model of switching dynamics in tantalum oxide memristive devices,” Appl. Phys. Lett., vol. 102, p. 223502, 2013;
61. M. Glusker, D.M. Hogan, and P. Vass; The ternary calculating machine of Thomas Fowler; IEEE Annals of the History of Computing, 2005;
62. N.P. Brousentov, S.P. Maslov, J. Ramil Alvarez, and E.A. Zhogolev; Development of Ternary computers at Moscow State University; Russian Virtual Computer Museum; 1997-2017;
63. G. Frieder; Ternary Computers, part 1: motivation for ternary computers; Micro 5 Conf. record of the 5th annual workshop on Microprogramming; 1972;
64. S. Ahmad, M. Alam; Balanced Ternary Logic For improving Computing; IJCSIT, 2014;
65. I. Profeanu; A ternary Arithmetic and Logic; WCE, June 2010;
66. M.G. Nektar, D.M. Hogan, P. Vass; The ternary calculating machine of Thomas Fowler; IEEE Annals of the History of Computing, Aug 2005;
67. E.W. Dijkstra; Notes on structured programming; EWD 249 Technical University, Eindhoven, Netherlands, 1969;
68. B. Cambou, P. Flikkema, J. Palmer, D. Telesca, C. Philabaum; Can Ternary Computing Improve Information Assurance?; MDPI, Journal cryptography, Feb 2018;
69. D.M. Miller, and M.A. Thornton; Multiple Valued Logic: Concepts and Representations; Synthesis Lectures on Digital Circuits and Systems; Morgan & Claypool Publishers, 2007;
70. S. Ahmad, and M. Alam; Balanced Ternary Logic For improving Computing; IJCSIT, 2014;
71. P.G. Flikkema and B. Cambou; Adapting Processor Architectures for the Periphery of the IoT Nervous System; IEEE 3rd World Forum on Internet of Things (WF-IoT), December 2016;
72. H. Gundersen; Aspect of balanced ternary arithmetic implemented using CMOS recharged semi-floating gate device; thesis Oslo Univ. 2008;
73. P.C. Balla, and A. Antoniou; Low Power Dissipation MOS Ternary Logic Family; IEEE J of Solid State Circuits, Oct 1984;
74. P.C. Balla, A. Antoniou; Low Power Dissipation MOS Ternary Logic Family; IEEE J of Solid State Circuits, Oct 1984;
75. X.W. Wu; CMOS Ternary Logic Circuits; IEE Proceedings, Feb 1990
76. P. Nagaraju, et al; Ternary Logic Gates and Ternary SRAM Implementation in VLSI; IJSR, Nov 2014;
77. N.P. Wanjari, S.P. Hajare; VLSI Design and Implementation of Ternary Logic Gates and Ternary SRAM Cell; IJECSE, April 2013;
78. A. Srivastava, and K. Venkatapathy; Design and Implementation of a Low Power Ternary Full Adder; VLSI design, vol 4, No.1, 1996;
79. N.P. Wanjari, and S.P. Hajare; VLSI Design and Implementation of Ternary Logic Gates and Ternary SRAM Cell; IJECSE, April 2013;
80. Anuj Gupta, May 2005, Implementing Generic BIST for testing Kilo-Bit Memories; Master Thesis No-6030402 Deemed University Patiala India

(Click Here)

(Click Here)