A Review of Topological Semimetal Phases in Photonic Artificial Microstructures

Introduction

In the last 2 decades, artificial microstructures including metamaterials and photonic crystals have attracted enormous interest because they provide great possibilities for manipulating optical waves. By judiciously modulating their structural parameters, novel physical phenomena and functionalities can be archived such as negative refractive index [1, 2], invisibility cloaks [3], and giant chiral response [4]. Optical metamaterials also promise an effective way for miniaturization and integration of optical devices. They have shown significant advantages in many practical application areas, such as optical holograms [5], sub-diffraction imaging [6], and the design of integrated multifunctional optical devices [7]. Over the last decade, the concept of topology has been extended from condensed matter physics to various systems including photonics, acoustics [8], mechanics [9, 10], and cold atoms [11]. As an optical dimension, topology characterizes the quantized global behavior of wave functions in contrast to other optical dimensions like amplitude, polarization, phase, or frequency. A topological phenomenon which does not change under continuous deformation can provide a robust way to control photons, yielding application in polarization control [12], lossless waveguides, lasers [13], and cavities. Based on the quantum Hall effect [14, 15], anomalous quantum Hall effect [16], quantum spin Hall effect [17], and valley Hall effect [18, 19], topological protected photonic waveguides have been proposed in the two-dimensional (2D) space, leading to the emerging research field of topological photonics [20–23].

With the development of research and experimental technique, topological photonics has further expanded to 3D [24]. Among the 3D topological states, topological semimetals have attracted much attention recently as the topological gapless phase, which possess topologically protected surface states and novel topological transport phenomena [25]. Gapless band structures such as Weyl points, spin-1 triple points, 3D Dirac points, and nodal lines or surfaces have been discussed in the photonic systems. The topological semimetal phase or gapless phase is fundamentally different from the 2D cases. Unlike the 2D Dirac points which can be easily removed if either time reversal symmetry (T) or inversion symmetry (P) is broken, the Weyl points as the fundamental band structure in 3D are stable in systems lacking T or P. Weyl points and other nodal points can carry non-trivial topological charge and give rise to topological Fermi arc surface states. Although there are a number of reviews covering the progress in topological photonics, approaches to photonic topological semimetals have been considered a minor subject of these reviews [26, 27]. Therefore, this review is focused on photonic topological semimetals and their applications.

In this review, we follow the fast progress in 3D topological photonic semimetal states. In the first part, we introduce the category of photonic semimetals, their topological invariant, and the condition to realize them. In the second part, we discuss the realization of photonic topological semimetals on approaches that use photonic crystals or metamaterials. Photonic Weyl points with T or P symmetry breaking, 3D Dirac points, nodal lines, and nodal surfaces are elucidated. In the last part, we introduce emerging applications including vector beam generation, chiral zero modes, and non-Hermitian effects.

3D Topological Semimetal Phases

The milestone of topological physics dates back to the discovery of quantum Hall phases, where 2D electron gas under a perpendicular magnetic field has quantized Hall conductance [28]. Because the magnetic field broke T, electrons in the quantum Hall effect propagate one way along the boundary, generating the chiral current. Backscattering is not allowed even with large defects because the edge states are topologically protected. The quantized feature of the Hall conductance is originated from the topological Chern number as follows:

where $F_n=i\nabla \times \langle u_n\left(\mathbf{k}\right)|{\nabla }_{\mathbf{k}}|u_n\left(\mathbf{k}\right)\rangle$ is the Berry curvature of the nth band and u_n is the nth eigenstate. The number of gapless edge modes inside a bandgap is determined by the difference of gap Chern number, which is the summation of all band Chern numbers below the bandgap, also known as the bulk-edge correspondence. When T is broken with magnetic field, the photonic quantum Hall effect can also emerge in photonic crystals composed of magnetoelectric or gyromagnetic materials [14, 15, 28–30]. The magnetoelectric materials have cross-coupling between electric and magnetic fields, where the constitutive relations take the form of $\mathbf{D}=\widehat{\mathrm{ϵ}}\mathbf{E}+\widehat{\chi }\mathbf{H}$ and $\mathbf{B}=\widehat{\mu }\mathbf{H}+\widehat{\zeta }\mathbf{E}$. For example, Jacobs et al. demonstrated that non-trivial band topology can be realized in Tellegen photonic crystals with a diagonal magnetoelectric response [30]. In contrast, the gyromagnetic materials do not have cross-coupling between electric and magnetic fields [14], where the permeability tensor takes the form as $\widehat{\mu }=\left[\begin{array}{ccc}\mu & i\kappa & 0\\ -i\kappa & \mu & 0\\ 0& 0& {\mu }_0\end{array}\right]$. Other photonic systems also use Floquet-like couple waveguides [31] and dynamic modulation [32] to mimic the quantum Hall effect.

Although the T-broken photonic systems have excellent one-way transport properties, it is difficult to realize or industrialize. Instead, T-invariant systems utilizing the quantum spin Hall effect have provided a solution without applying magnetic field or gyromagnetic materials. The quantum spin Hall state can be viewed as two copies of the quantum Hall state for each spin. Each spin is a lock to one helical edge state. Elections with spin up or spin down will generate an edge current of counterclockwise or clockwise, or vice versa. As the Chern number of each spin cancels with each other, the total Chern number of quantum spin Hall system is trivial. The topology in the quantum spin Hall effect is characterized by the Z₂ invariant [33], where the trivial and non-trivial Z₂ invariants are 0 and 1, respectively. The quantum spin Hall effect has been realized with 2D array of resonators [16], photonic crystals with crystalline symmetries [17], and bianisotropy-induced photonic topological insulators [34, 35].

Now, we introduce the 3D topological semimetals and show how they relate to the non-trivial topological invariant. Weyl points acting like relativistic fermionic particles with vanishing mass are featured as point degeneracies among two bands in the 3D momentum space. Linear dispersion around the Weyl point is governed by the Weyl Hamiltonian $H={\nu }_x{k}_x{\sigma }_x+{\nu }_y{k}_y{\sigma }_y+{\nu }_z{k}_z{\sigma }_z$, where ${\nu }_{x,y,z}$ are group velocities and ${\sigma }_{x,y,z}$ are Pauli matrices. Weyl points as the most fundamental topological structure in 3D crystals, usually occurring in pairs and can be viewed as monopoles with quantized source of Berry flux. By integrating the Berry curvature in a 2D surface enclosing a Weyl point, the Chern number as the topological charge of Weyl point can be obtained. Weyl points are virtually indestructible against perturbations in a 3D momentum space, unless a pair of Weyl points with opposite topological charge annihilate with each other. The topological character of Weyl points is reflected in the appearance of topologically protected states on the surface. The equifrequency contours of the surface states are open arcs connecting the surface projections of Weyl points with opposite topological charges, which are known as the Fermi arcs, as shown in Figure 1A. Topologically protected surface states in topological semimetals are immune to a special kind of obstacles and defects, resulting in the non-reflective transmission of wave modes. For those systems with a momentum gap along the $k_z$ direction, a line defect or obstruction which is translation invariant along the z direction can preserve the $k_z$ wavenumber of the scattering waves, prohibiting the chiral surface modes from scattering into the bulk or other surface modes inside different momentum gaps. As shown in Figure 1B, the topological charge of a bulk Weyl node can be reflected by the connectivity of Fermi arcs according to Nielsen-Ninomiya no-go theorem. For a charge-2 Weyl point with quadratic dispersion, there are two branches of Fermi arcs connecting the Weyl point. Figure 1C shows the fourfold 3D Dirac points which are symmetry-protected Z₂ monopoles in the 3D momentum space. Two branches of spin-polarized Fermi arcs can connect the Dirac point pair in the Brillouin zone. Other form of semimetal band structure has also been realized in photonics, such as nodal line [36, 37] and nodal surface [38]. The nodal line contains topological features as the Berry phase of π around the node. Recent studies have shown that nodal lines can carry a non-trivial Chern number as the Weyl points [37] or carry non-trivial Z₂ charge as the 3D Dirac points [28]. Nodal surfaces can also carry non-trivial Chern number in systems with non-symmorphic symmetries and T [39].

FIGURE 1. (A) Pair of charge-1 Weyl points linked by a Fermi arc in the momentum space. The Weyl points have a cone-like linear dispersion. On equifrequency contour (gray plane), the surface states form an open arc linking the projection of Weyl points. (B) Charge-2 Weyl point (middle) linked with two charge-1 Weyl points. (C) A pair of 3D Dirac points as Z₂ monopoles linked by two branches of Fermi arcs.

Realization of 3D Photonic Topological Phases

Weyl Point With T-Breaking

Weyl points in 3D materials can be achieved by breaking either T or P. Here, we focus on the realization of photonic Weyl points achieved by the T-breaking approaches. For the Weyl points in electron systems with T-breaking, several novel topological properties are supported, such as axial anomaly [40], chiral anomaly [41, 42], gravitational anomaly [43], giant photocurrent [44], and quantum oscillation phenomena [45]. Lu et al. theoretically proposed that the breakthrough for achieving Weyl points with T- and/or P-breaking occurred in gyroid photonic crystals at infrared wavelengths. However, the realization of T-breaking in the photonic system usually relies on the magneto-optical effect, while the magneto-optical response of existing optical materials, such as ferromagnetic materials, is weak in the microwave frequencies and cannot cover the optical domain [46]. Although a considerably simple approach has been earlier proposed theoretically by Yang et al. in a magnetic tetrahedral photonic crystal [47], the experimental observation for the T-breaking Weyl point based on magnetic materials had not been realized until very recently due to the difficulty of fabricating the 3D structure in magnetic materials [48]. In addition, several theoretical works proposed recently that T could be broken in plasma [49, 50]. A new scheme shows that the plasma may support Weyl points in the T-breaking photonic system when an external magnetic field is applied [51]. Subsequently, Wang et al. experimentally observed photonic Weyl degeneracies in magnetized plasma at the terahertz regime, and the corresponding photonic Fermi arcs have also been demonstrated [52]. In this section, we review the main numerical and experimental schemes of 3D photonic topological Weyl points based on T-breaking system, including gyroid photonic crystals and magnetized plasmas.

The 3D photonic Weyl points with T-breaking were first theoretically predicted in double gyroid (DG) photonic crystals. The corresponding real-space structure in a unit cell consisting of a single gyroid (SG) and its inversion counterpart is shown in the Figure 2A [24]. The band structures of SG and DG photonic crystals are donated by red and blue lines, respectively, as shown in Figure 2B. The DG photonic crystal band structure exhibits a threefold quadratic nodal point as highlighted in green ellipses. When two air spheres are introduced in the DG photonic crystal without breaking P or T, the trivial threefold quadratic nodal point is transformed into a trivial twofold nodal ring. Starting with the twofold nodal ring, Weyl points are introduced by breaking P or T. P-breaking is done by adding an air sphere only in an SG, leading to the appearance of two pairs of Weyl points, as shown in the band structure plotted in Figure 2C. T-breaking is realized by adding an external magnetic field to the DG photonic crystal composed of a gyroelectric material. The band structure for only T-breaking is plotted in Figure 2D where only one pair of Weyl points appears in contrast to the P-breaking case. In the T-breaking system, P maps a Weyl point at k to −k with reversed chirality, while in the P-breaking system, T maps a Weyl point at k to −k with the same chirality. Because the net Berry flux integrated over the Brillouin zone must vanish, the net chirality of Weyl points must be zero. Therefore, a T-breaking system can only have one pair of Weyl points, while a P-breaking system should possess even pairs of Weyl points to neutralize the whole system. A single pair of photonic Weyl points with T broken was observed very recently based on a gyromagnetic photonic crystal operating at microwave frequencies [48]. The unit cell of the photonic crystal consisting of a gyromagnetic rod and a metallic plate perforated with holes is shown in Figure 2E. An external static magnetic field is applied along the z-axis to break T in the gyromagnetic photonic crystal. By increasing the strength of the external magnetic field, one pair of photonic Weyl points is generated and then annihilated, which means the system transits into a topological semimetal phase and then the topological insulator phase. With a 0.2 T biasing magnetic field, the band structures of one pair of ideal Weyl points with opposite topological charge at the same frequency in Brillouin zone are shown in Figure 2F. The Fermi arc connecting the surface projections of this pair of Weyl points with opposite topological charges is measured experimentally, as shown in Figure 2G. With distinct k_z cases, the measured projected band structures corresponding to topological transition are shown in Figure 2H, where the Fermi arc exists only in the range of $k_z=0$ to $k_z=0.53\pi /h$.

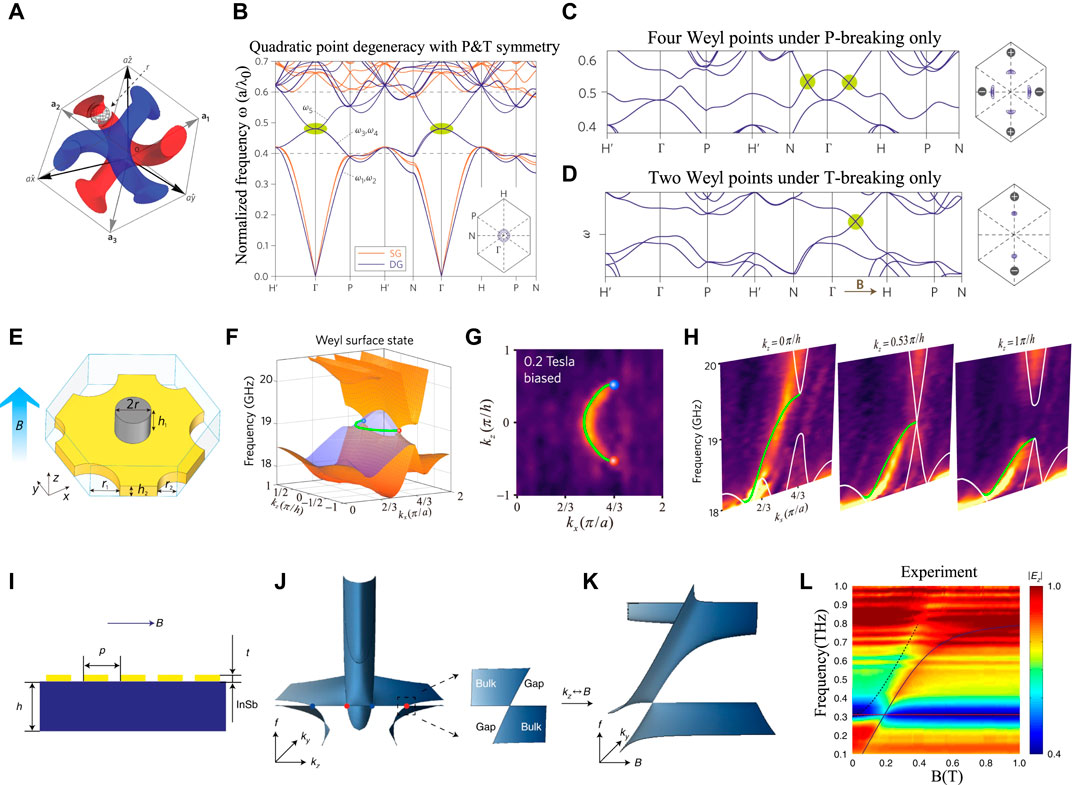
FIGURE 2. 3D photonic Weyl semimetals by breaking T [24]. (A) The unit cell of double gyroid (DG) photonic crystals. (B) The band dispersion of original DG photonic crystal (blue line) and single gyroid (SG) photonic crystal (red line). (C) The band structure with only P-breaking by placing one air-sphere in only one gyroid, where two pairs of Weyl points appear. (D) The band structure with only T-breaking by applying a magnetic field to the DG photonic made of gyroelectric material, where one pair of Weyl points appears. (E) The unit cell of the gyromagnetic photonic crystal [48]. (F) Simulated band structure under a magnetic field of 0.2 T. The Fermi arc is donated by a green line. (G) Measured surface projections of single pair of Weyl points and the associated Fermi arc. (H) Measured surface dispersions on the front surface for $k_z=0$, $k_z=0.53\pi /h$, and $k_z=\pi /h$, respectively. (I) Schematics of the sample with a metal grating on the top of the InSb substrate [52]. (J) Simulated band structure of the magnetized plasma with B = 0.19 T. (K) Simulated band structure with $k_z$ substituted by B. (L) Experimentally measured reflection spectra.

Another experimental observation of Weyl points in the T-breaking photonic system was realized in magnetized plasma at the terahertz regime when an external magnetic field is applied. Figure 2I shows the sample with a metal grating to compensate for the phase mismatch on the top of the InSb substrate. For a semiconductor InSb, the band structure under a magnetic field strength of B = 0.19 T is plotted in Figure 2J. The band structure shows four Weyl points with opposite chiralities donated by red and blue spheres. The projected band structure around one Weyl point is shown on the right side of Figure 2J. Since magnetic field strength B behaves similarly with $k_z$ in the effective Hamiltonian as well as in constructing the band structure of the Weyl points, a parameter space was constructed by scanning B, instead of $k_z$, in order to facilitate the observation. The band structure constructed in the synthetic parameter space $\left[k_x,k_y,B\right]$ is shown in Figure 2K, where linear dispersion demonstrates the presence of Weyl points. By varying the magnetic field strength from 0 to 1T, the reflection spectrum was measured, as shown in Figure 2L, which agrees well with the theoretical results in Figure 2K.

Weyl Points With P-breaking

P-breaking can be realized by specially designed structures, while an external or synthetic magnetic field is often required to break T. For example, using a periodic layered structure in the all-dielectric system can break only P to realize Weyl points [53]. In this section, we review Weyl points in photonic crystals and metamaterials by breaking P.

Weyl points were experimentally observed at microwave frequencies by using a 3D DG photonic crystal with broken P [54]. The P-breaking DG is shown in Figure 3A. Because T is preserved in the system, there are even pairs of Weyl points. Figure 3B shows two pairs of Weyl points in the (101) plane of the Brillouin zone. To observe the Weyl points, angle-resolved transmission measurement was used to probe the dispersions of the 3D bulk states. The bulk states of the k vectors can be excited with an incident wave with an incidence angle θ, as shown in Figure 3C. While maintaining the rotation angle of the samples $\alpha ={90}^{\circ }$, the beam scans through the upper Weyl points along $\Gamma -H$. The experimental data and calculated band structures projected along the (101) plane clearly show a type-I Weyl point along $\Gamma -H$, as shown in Figure 3D. Type-I Weyl points have also been observed at optical frequencies in a photonic crystal coated with layered-composite nanometric materials [55].

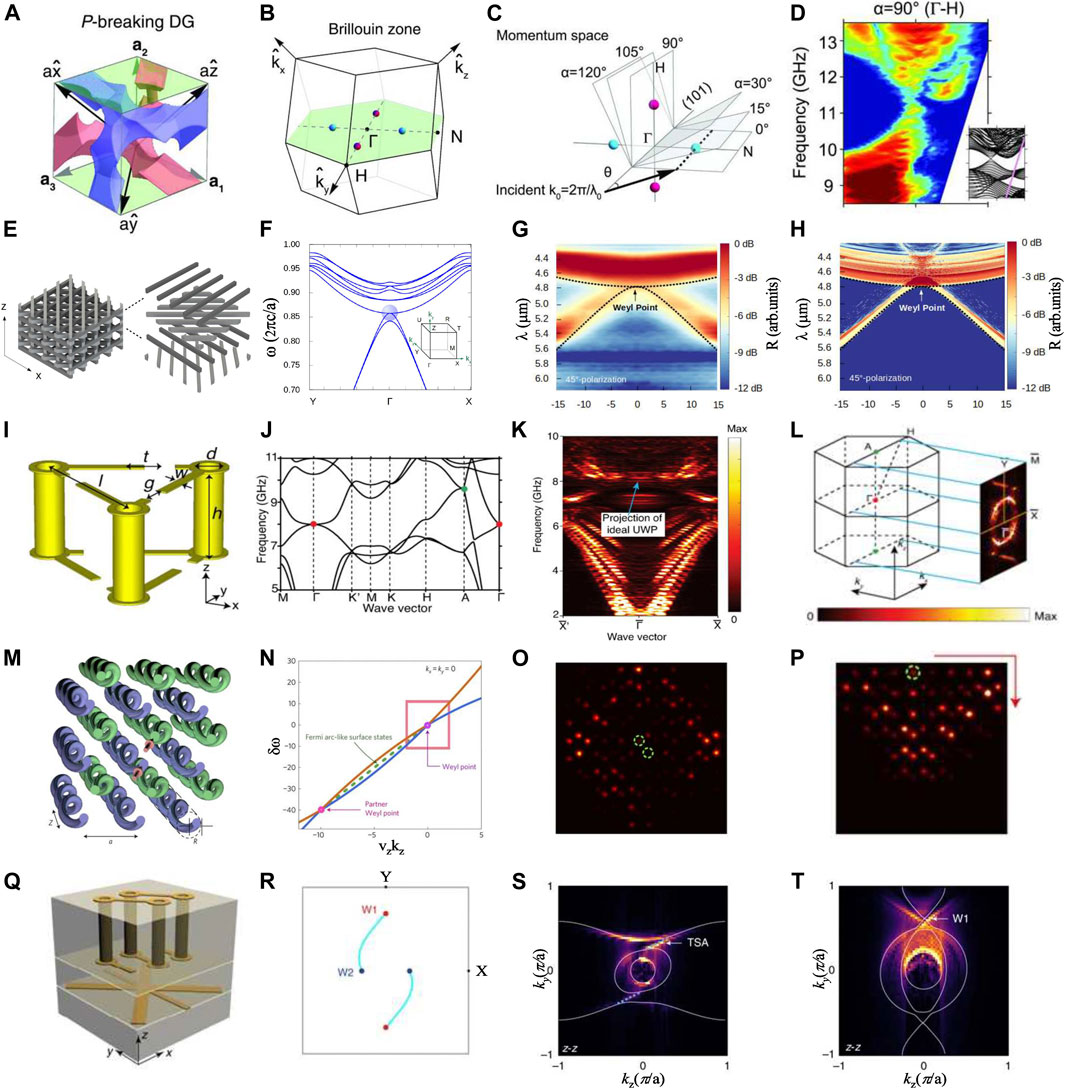
FIGURE 3. (A) bcc cell of the P-breaking double gyroid photonic crystal [54]. (B) Two pairs of Weyl points are illustrated on the green (101) plane along Γ-H and Γ-N in the Brillouin zone. (C) The different bulk states can be excited by changing the incidence angle θ of the incident wave. (D) Experimental results of the Weyl point along the Γ-H direction. (E) Schematic diagram of the chiral woodpile structure [58]. (F) The band structure along the Y-Γ-X and the Weyl point is illustrated with a blue circle. (G) and (H) experimentally measured and simulated reflection spectra showing Weyl point for 45° polarizations, respectively. (I) The unit cell of the chiral metamaterial [63]. (J) Weyl points are denoted by red and green dots in the band structure. (K) Measured projected band diagram on the k_x–k_z plane. (L) Measured surface dispersion obtained by Fourier transformation. (M) Schematic diagram of the waveguide array structure [64]. (N) The dispersion diagram in the δk_x–δk_z plane when δk_x = δk_y = 0 shows the type-II Weyl points and Fermi arc–like surface states. (O) Experimental results of the intensity plots at the output facet at a = 27 μm, λ = 1,525 nm, and conical diffraction demonstrates the existence of type-II Weyl points. Green circles: position of input waveguides. (P) Experimental results of the intensity plots at the output facet at a = 27 μm, λ = 1,500 nm demonstrate the presence of Fermi arc–like surface states. Green circles: position of input waveguides. (Q) Schematic diagram of the unit cell of chiral hyperbolic metamaterials [71]. (R) Surface band structure on a varying frequency k_x–k_y map. (S) and (T) Experimental results of the topological surface-state arcs and type-II Weyl points in the momentum space at 5.46 GHz, respectively.

If the Weyl system has additional spatial symmetries, Weyl points with higher topological charge can appear at high symmetry points in the Brillouin zone [51, 56]. Charge-2 Weyl points can exist in a chiral woodpile photonic crystal with screw symmetry [57]. Recently, a parity-breaking chiral woodpile photonic crystal fabricated by two-photon polymerization was constructed to observe a charge-2 Weyl point in the mid-infrared regime [58]. Each layer rotates ${45}^{\circ }$ next to the neighboring layer, as shown in Figure 3E. The Weyl point with quadratic dispersion occurs at the Г point, as shown in Figure 3F; Figure 3G shows the experimental observation of charge-2 Weyl points using the angle-resolved Fourier-transform infrared spectroscopy, in contrast to the simulated angle-resolved reflection spectra in Figure 3H. With a similar woodpile structure, not only Weyl points can be realized but also negative refraction can be observed in phononic crystals [59]. Weyl points with higher topological charge are also reported in metallic photonic crystals in microwave frequencies [60], acoustic structure [61], and transition-metal monosilicides [62].

Weyl points with higher topological charge exist not only in photonic crystal but also in chiral metamaterials [63]. Topological charge-2 ideal Weyl points were reported in the chiral microwave metamaterial which has C₃ rotational symmetry and time-reversal symmetry. The unit cell consists of three double-split ring resonators, as shown in Figure 3I. The Weyl points with a topological charge +2 at Γ point and −2 at A point are enforced by chiral symmetry. The band structure of the system is shown in Figure 3J. The measured projected band structure of the k_x–k_z plane along the high-symmetry line $\overline{X}\prime \overline{X}$ shows the ideal Weyl point, as depicted in Figure 3K. The crossing bands are quadratic in the k_x–k_y plane and linear in the k_z direction. Because the topological charge is 2, there are two Fermi arcs connecting the oppositely charged Weyl points, as shown in Figure 3L. Weyl points carrying higher topological charges have exotic topological properties; for instance, the Fermi arcs can extend over most of the Brillouin zone.

In addition to type-I Weyl points, type-II Weyl points are also observed in the experiment. The dispersion around type-II Weyl points is strongly tilted in contrast to type-I Weyl points, where the group velocities of the two crossing bands have the same sign along one direction [64]. Noh et al. observed type-II Weyl points at optical frequencies and Fermi arc–like surface states in a 3D photonic crystal structure of coupled single-mode waveguides [65]. The helical waveguides made by femtosecond direct laser writing are shown in Figure 3M. The partner Weyl point is associated with Fermi arc–like surface states, as shown in Figure 3N. When the lattice constant is a = 27 um, the conical diffraction pattern was clearly observed at the frequency of 1,525 nm, confirming the existence of type-II Weyl point, as shown in Figure 3O. The Fermi arc–like surface states in the experiment are shown in Figure 3P. Type-II Weyl points have also been found in acoustic systems [66, 67].

Another mechanism to break P is realized by combining chiral and hyperbolic properties in metamaterials [38, 68–70]. Yang et al. experimentally observed type-II Weyl points and photonic topological surface state arcs in a chiral hyperbolic metamaterial by near-field scanning measurements [71]. The cubic unit cell is shown in Figure 3Q. The unit cell has three layers as follows: the top layer is a chiral layer, the middle layer is a blank layer, and the bottom layer is a hyperbolic layer. Topological surface states connecting two pairs of Weyl points in the frequency-varying k_x–k_y plane are shown in Figure 3R. Topological surface state arcs and type-II Weyl points observed in the experiment are shown in Figures 3S,T, respectively. In addition, disorder in chiral hyperbolic metamaterials can induce topological state transition in the photonic Weyl system [72]. The combination of Weyl points and metamaterials has greatly enriched the field of the topological semimetal phase and brings new potential to the manipulation of electromagnetic and acoustic waves.

3D Dirac Point

Hosting a fourfold linear dispersion in the 3D momentum space, the 3D Dirac point represents the degeneracy of paired Weyl points with opposite chiralities. In photonics, fourfold degeneracy of the Dirac point can be achieved through additional symmetries, such as electromagnetic duality symmetry and space symmetries. While 3D Dirac points carry a trivial Chern number, they are $Z_2$ monopoles in the 3D momentum space [73]. Upon symmetry breaking, the band structure can transit into the $Z_2$ nodal ring, Weyl dipole, and topological bandgap supporting gapless surface states [74] or hinge states [75]. Recently, the transition from the 3D Dirac point to Weyl dipole is experimentally demonstrated in acoustics [76].

3D Dirac points can be classified into symmetry-enforced Dirac points and band inversion Dirac points according to the mechanism in forming the fourfold degeneracy. Symmetry-enforced Dirac points are unavoidable results of the non-symmorphic space group of a material. The first proposed photonic 3D Dirac photonic crystal has glide reflections in x, y, and z directions, as shown in Figure 4A [74]. The 3D Dirac points which host linear dispersions appear at high-symmetry P points of the Brillouin zone, as shown in Figure 4B. The glide symmetries together with time reversal symmetry not only stabilize the Dirac point but also prevent the anti-crossing of helicoid surface states, leading to the non-trivial band topology on the surface. As an example, quad-helicoid surface states are observed in acoustics [28, 77].

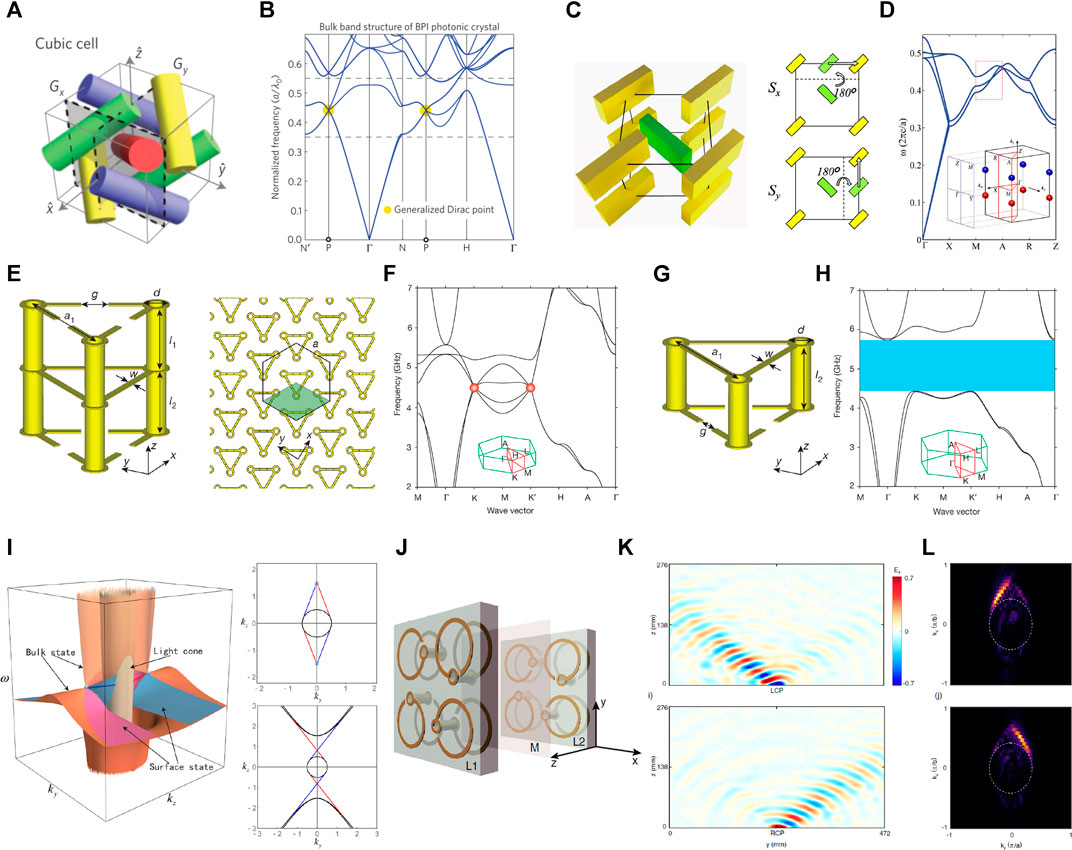
FIGURE 4. (A) Photonic crystal with glide reflection in x, y, and z directions [74]. (B) Band structure with a single 3D Dirac point. (C) 3D Dirac photonic crystal with screw symmetries and (D) its photonic band structure [78]. (E) 3D array of metallic split-ring resonators with 3D Dirac point [79]. (F) Band structure of the photonic crystal with the unit cells in (E). (G) Unit cell giving rise to a 3D topological bandgap through removing the top three split-ring resonators. (H) Band structure of the photonic topological insulator with the unit cells in (G). (I) Bulk and surface state dispersions of a Dirac metamaterial with electromagnetic duality symmetry [81]. Equifrequency contour at above (top-right) and below (bottom-right) the Dirac point frequency. (J) Printed circuit board unit cell and spin-polarized topological surface states of a Dirac metamaterial (K) in the real and (L) momentum space [82].

Meanwhile, band inversion 3D Dirac points have been discovered in photonics utilizing screw symmetries [78], hexagonal structures with C₃ or C₆ symmetry [79, 80], and electromagnetic duality symmetry [81, 82]. These 3D Dirac points lie on the generic momenta of an axis of rotation symmetry, always come in pairs, and can be eliminated through merging and pairwise annihilation. The locations of the band crossings can be continuously tuned as a function of the Hamiltonian control parameters. Figure 4C shows a type-II 3D Dirac photonic crystal with screw symmetries. Photonic Kramers double degeneracy of p and d states is generated by anti-unitary operators composed of the screw symmetry and T. The crossing of p and d states forms the fourfold degeneracy, as shown in Figure 4D. For hexagonal structures with C₃ symmetry (Figure 4E), the photonic band structure exhibits frequency-isolated 3D Dirac points for fine-tuned lattice parameters, as shown in Figure 4F. When removing the upper three split-ring resonators in the unit cell, the photonic metamaterial becomes a weak insulator (Figures 4G,H), which supports the robust interface state with cone dispersion. Overall, the band inversion Dirac points are formed with less symmetry elements and may provide an option to realize strongly anisotropic dispersion.

Electromagnetic duality symmetry is an internal symmetry of the electromagnetic field [81, 82]. The realization of this symmetry requires the proportionality between permittivity and permeability tensors, which indicates that metamaterials described by the effective medium theory are preferred. Due to the electromagnetic duality, circular polarizations are the eigenstates of the system. For left-handed circularly polarized (LCP) photons, one Dirac point behaves like a sink of Berry flux, while for right-handed circularly polarized (RCP) photons, it behaves like a source. As a result, two pairs of spin-polarized surface states appear at the interface between metamaterial and air, as shown in Figure 4I. In the experiment, fine-tuned metallic helical elements are used to introduce both electric and magnetic resonances in the microwave regime, as shown in Figure 4J. The spin-polarized topological surface states in the real and momentum space were experimentally demonstrated in Figure 4K and Figure 4L, respectively. This spin–orbit coupling character may bring about a unique advantage in the manipulation of light.

Nodal Line and Nodal Surface

Nodal lines protected by P and T symmetries are treated as the 3D extrusion of 2D Dirac points. They share the same local Hamiltonian $H\left(\mathbf{k}\right)=k_x{\sigma }_x+k_z{\sigma }_z$. The Berry phase around the nodal line is π. Due to the periodicity of the Brillouin zone, a single nodal line forms a closed ring. The Berry curvature vanishes under P and T symmetries, and the nodal line is not charged. The breaking of P or T in the nodal line can give rise to the phase transition to Weyl points [24]. Nodal rings can intersect and form nodal chains under the local chain Hamiltonian $H\left(\mathbf{k}\right)=k_x{\sigma }_x+\left(k_y{k}_z+m_z\right){\sigma }_z$ when the mass term $m_z=0$. Nodal chains are experimentally observed in a metallic mesh photonic crystal [83], as shown in Figure 5A. These nodal chains are protected by mirror symmetry and have little frequency variation. The linear crossing of the third and fourth bands forms the line degeneracies of nodal chains, as shown in band structures in Figures 5B,C.

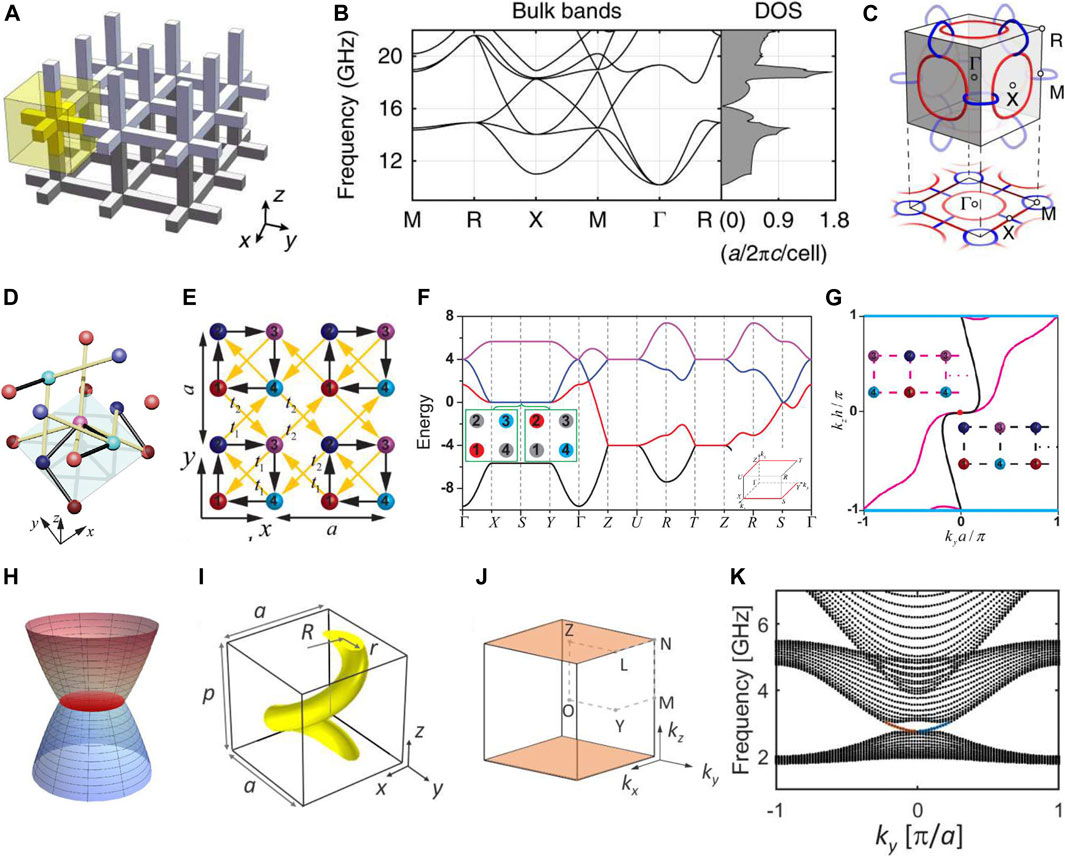
FIGURE 5. (A) Schematic illustration for nodal chain photonic crystal [83]. (B) The bulk band structure and density of states. (C) The structure of nodal chains in the Brillouin zone. (D) Tight binding model for a charged nodal line [37]. (E) The projection of the tight binding model on the x–y plane. (F) The band structures with charged nodal lines are formed by geometric frustration. (G) Equifrequency contour on the k_y–k_z surface Brillouin zone. The red dot and cyan line represent the projection of the charged +2 Weyl point and the charged -2 nodal chain. (H) Schematics of a nodal surface [38]. (I) Schematic of a unit cell of the nodal surface photonic crystal. (J) Brillouin zone with the high-lighted nodal surface. (K) Surface state dispersion at $k_x=0$ and $k_z=0.5\pi /p$.

To obtain a charged nodal line, X. Meng et al. considered a simple Hamiltonian $H\left(\mathbf{k}\right)=k_x{\sigma }_x+k_z{\sigma }_z+k_{\rho }{k}_y{\sigma }_y$ [37], where $k_{\rho }=\sqrt{k_x^2+k_z^2}$. The Hamiltonian possesses a nodal line along the y direction as the bands are degenerate at $k_{\rho }=0$ and exhibits linear dispersion away from this nodal line. The quantized Berry charge carried by the nodal line is 1. The tight binding model of the charged nodal line is proposed using the concept of geometric frustration, as shown in Figures 5D,E. Two types of couplings are denoted as black and yellow bonds, respectively. Black bonds occur between adjacent layers, while yellow bonds occur between next adjacent layers. Figure 5F shows the band structure of this tight binding model, where perfect flat bands of nodal chains are found. The charged nodal chains give rise to the existence of chiral edge states, as shown in Figure 5G. In addition to the nodal line with a non-trivial Chern number, the Z₂ nodal line may exist in photonic crystals with glide reflection and T [28].

Nodal surfaces are degeneracies in two dimensions, as shown in Figure 5H. M. Kim et al. proposed a nodal surface metamaterial with twofold screw symmetry S_2z and T [38]. The metamaterial is composed of metallic helices, as shown in Figure 5I. The hyperbolicity and chirality of the metamaterial give rise to the topologically non-trivial phase; thus, the nodal surface carries a non-trivial topological charge of Chern number. The nodal surface is formed between the first and the second bands at $k_z=\pi /p$, as shown in Figure 5J. Surface modes exist according to the bulk–boundary correspondence, as shown in Figure 5K at $k_x=0$ and $k_z=0.5\pi /p$.

Application in Manipulating Light

Winding Phase and Vector Beams Generation

The non-trivial topology of photonic semimetals can be revealed not only by the surface states but also by the vortical phase profile in the reflection of spin-polarized electromagnetic waves. Cheng et al. demonstrate the vortical phase and the generation of vortex beam using the reflection property of Weyl metamaterials [84]. As shown in Figure 6A, an incident Gaussian beam with left-handed polarization can be reflected into a vortex beam with right-handed polarization. The Weyl metamaterial constructed by a metallic saddle-shaped connective coil has four ideal Weyl nodes in the Brillouin zone. When light is incident with a certain elevation angle φ and varies with an azimuthal angle θ, the winding number of the scattering matrix, which is 2 in 2π of phase, is equivalent to the projected topological charge enclosed by k₀sin (φ) in the surface Brillouin zone, as shown in Figure 6B. To reveal the topological property of the reflected wave, a scattering matrix combined with four s and p polarizations is measured for varying azimuthal angle θ. It has been proven that the scattering matrix is topologically equivalent to the Hamiltonian. Two microwave horn antennas are used as a transmitter and a receiver, as shown in Figure 6C. The topological feature of the Weyl metamaterial is that each eigenstate’s reflection phase winds 2π, and eigenpolarizations wind π for a full turn of rotation, as shown in Figure 6D. In an ideal case where the metamaterial and air are matched with the same impedance, the scattering matrix around the Weyl point is given as follows:

The scattering matrix operated on the right-handed circular polarization state $|R\rangle$ is converted to the left-handed polarization state $|L\rangle$ with and an extra 2θ phase, while the conversion from $|L\rangle$ to $|R\rangle$ is without the extra phase. Therefore, a Gaussian beam with right-handed polarization would be converted in to a vortex beam with an orbital angular momentum of 2 upon reflection. In the experiment, a right-handed elliptical incident beam described in Figure 6E would give rise to a winding reflection phase of 4π, as shown in Figure 6F. The winding phase also gives rise to the spiral Fermi arc, as shown in Figure 6G.

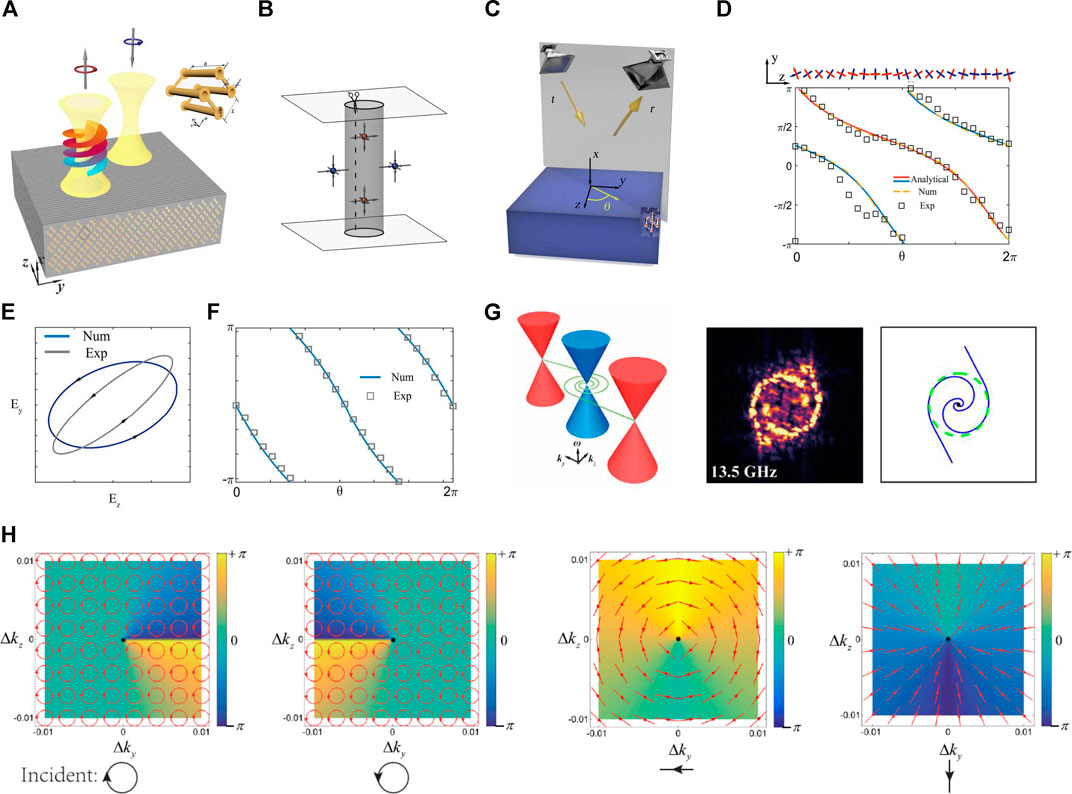
FIGURE 6. (A) Vortical mirror in Weyl metamaterial is composed of metallic saddle-shaped structure, and an incident Gaussian beam can be reflected into a vortex beam [84]. (B) Weyl nodes with arrows indicating the directions of the Berry curvatures. Cylindrical surface enclosing the Weyl points has a topological charge of 2. (C) Reflection measurement setup in a microwave. (D) Reflection phases of the eigenstates and the eigenpolarizations of the Jones matrix for incident light. (E) An incident beam with the right-handed elliptical polarization state gives rise to (F) 4π phase winding, generating a vortex beam. (G) Spiral Fermi arcs formed by reflection between the Weyl metamaterial and perfect electric conductor. (H) Reflection spectrum around a 3D Dirac metamaterial [81].

The angle-resolved reflectance spectrum also shows how a Dirac node can be decomposed into two related Weyl points with opposite topological charge [81]. As shown in Figure 6H, an anticlockwise loop in the momentum space around the Dirac point with RCP or LCP incidence acquires a 2π or −2π reflection phase, when circular polarizations are the eigenstates of the system with electromagnetic duality. Moreover, symmetrical angular and radial vector beams are generated by a Gaussian beam incidence with TE and TM polarization states. In contrast to conventional vector beam generators that rely on spatially varying phase elements, Weyl and Dirac metamaterials which are alignment-free may establish a new way to generating vector and vortex beams.

Chiral Zero Mode for Bulk Transport

Owing to the chirality of Weyl points, the Weyl or 3D Dirac crystal can support one-way chiral zero modes under a strong magnetic field, which leads to non-conservation of chiral currents known as a chiral anomaly [85, 86]. The chiral zero mode is a one-way propagative bulk mode, which can be applied for the robust transport of photons in the bulk medium. In order to generate an effective field, shifting of the Weyl point positions is applied in the metamaterial [41], as shown in Figures 7A,B. The four Weyl points rotate around the z axis when rotating the metallic coil, as shown in Figures 7C,D, generating a pseudo-gauge field. The band structure is shown in Figure 7E, Landau levels for Weyl points with positive (negative) chirality support a chiral zero mode with a positive (negative) group velocity. This feature is observed in the Fourier transform results, as shown in Figure 7F, that zeroth Landau levels are up-propagating in Weyl points Q3 and Q4 while down-going in Q1 and Q2. Overall, the Weyl system provides a platform for examining the interesting features that appear under a magnetic field. It can also be applied for the robust transport of photons in the bulk medium. The mechanism to generate pseudo-gauge field in Weyl crystals has also been applied in acoustics [87].

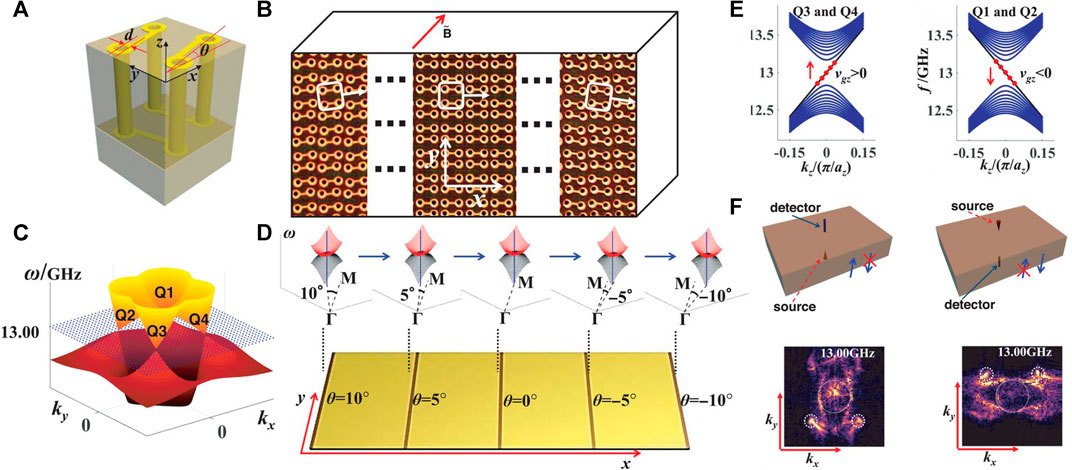
FIGURE 7. (A) Saddle-shaped metallic coil with rotation about z axis [41]. (B) Top surface of the sample. Gradient of rotational angle along the x direction generates a synthetic magnetic field along the z direction. (C) Dispersion of the Weyl metamaterial with no rotation angle. (D) The position of the Weyl point Q1 shifts as the rotation angle varies linearly with x. (E) Band structures showing Landau levels for Weyl points. (F) Experimental result for up-going (down-going) chiral zero modes around Weyl points Q3 and Q4 (Q1 and Q2).

Non-Hermitian Photonic Topological Semimetals

In the last few years, non-Hermiticity has been explored in topological materials such as topological insulators and Weyl semimetals [88, 89]. Photonic systems, which break Hermiticity through material absorption, gain, or radiative outcoupling, have a unique advantage to realize non-Hermiticity over the solid-state systems. Recently, the Weyl exceptional ring has been experimentally realized in a 3D photonic lattice composed of evanescently coupled helical waveguides [90], as shown in Figures 8A,B. The band structure of Weyl exceptional rings is shown in Figures 8C,D. To remove the Hermiticity of this system, periodic breaks are inserted into one of the two sublattices. The Weyl exceptional ring possesses quantized Berry charge–protected surface states, as shown in Figure 8E. The topological transition from Weyl points to Weyl exceptional rings is confirmed in the experiment by observing the appearance of Fermi arc surface states and the disappearance of conical diffraction for increasing break length. Various unconventional Weyl exceptional contours are also found in non-Hermitian chiral plasma, which can be achieved using metamaterials with effective constitutive parameters [91]. An unconventional Weyl point can transform into a quadratic Weyl exceptional circle, a type-I Weyl exceptional chain with one chain point, a type-II Weyl exceptional chain with two chain points, or other forms. Topological phase transition depending only on the strength of the non-Hermiticity allows for a new route to obtain tunable photonic topological materials [92].

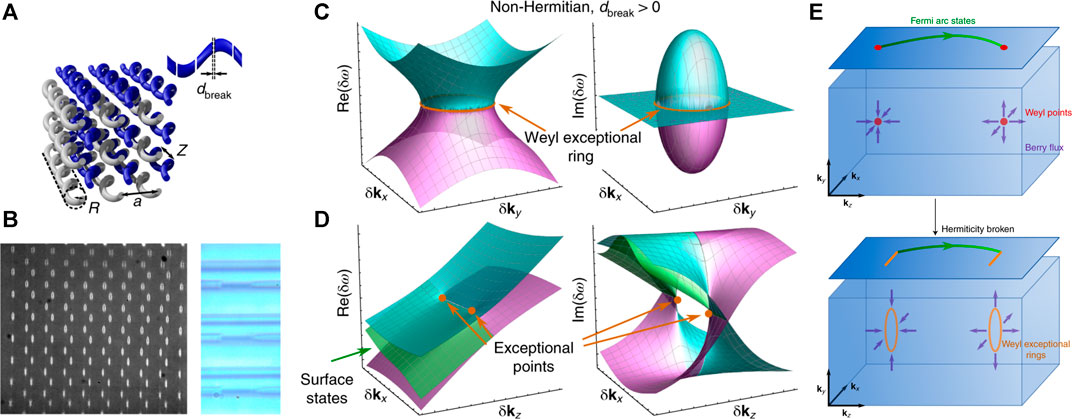
FIGURE 8. (A) Bipartite helical waveguide array, where breaks have been added to one of the sublattices to remove the Hermiticity [90]. (B) Image of the output facet (left) and microscope image showing breaks added (right). (C) Band structures in the $\delta k_x-\delta k_y$ plane possessing a Weyl nodal ring. (D) Band structures in the $\delta k_x-\delta k_z$ plane, exhibiting two exceptional points as the nodal ring intersects the plane twice. (E) Surface states convert to connecting the projection of Weyl exceptional rings with Hermiticity broken.

Prospective and Conclusion

The study of photonic topological semimetal has been developed very rapidly. Great success has been achieved in finding new exotic features exploiting the spin-1 nature of photons. Having a great designability in structural design with composite materials, the photonic topological semimetal provides a unique platform to study the chirality or spin-related effects. The application of topology in photonic artificial microstructure also gives a new way to manipulate light. The application area may cover the robust transport, negative refraction, and vector beam generation. Based on the topological semimetal phase, the 3D topological insulator phase can be achieved through symmetry breaking. The design of photonic topological semimetal may further cover the non-linearity [93], non-Hermiticity [88], and more synthetic field or synthetic space [94]. Very recently, 3D higher order topological semimetals were proposed with topological semimetals [95–99]. We believe that the photonic topological semimetals will continue to play an important role both in the theoretical study and application.

Author Contributions

BX and SC conceived the idea. BX, HL, and HW prepared the draft. All authors contributed to the discussion and revision of the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China (2016YFA0301102 and 2017YFA0303800), the National Natural Science Fund for Distinguished Young Scholar (11925403), the National Natural Science Foundation of China (12004198, 11974193, 91856101, and 11774186), Natural Science Foundation of Tianjin for Distinguished Young Scientists (18JCJQJC45700), and the China Postdoctoral Science Foundation (2020M680850).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References