Mass-Conservation Increases Robustness in Stochastic Reaction-Diffusion Models of Cell Crawling

1 Introduction

An intensive use of physical and mathematical theories on pattern formation in extended systems [1, 2], gave rise to valuable arguments to explain the formation of certain biological structures. Such mathematical mechanisms have permitted the modeling of processes on very different spatial and temporal scales: from the formation of the skin in fishes [3], to the definition of the direction in embryonic developing [4]. Such mechanisms have to be robust to small changes of parameters in order to be reliable. Robustness is a generic feature of living cells. It ensures that specific cellular functions are maintained despite external and internal change on the conditions. System control and feedback control are some of the characteristic mechanisms that allow robustness [5, 6].

Cell migration is an example of robust phenomenon that is present both in prokaryotic and eukaryotic cells. Living cells migrate to perform different tasks such as food targeting, wound healing and immune response. Independently of the presence of an external signal, before moving, cells need to define the direction to follow. To do so, they first define the front and the back of the cell. The process of formation of a polar direction inside a single cell is commonly known as cell polarization [7] and it is a typical example of pattern formation at the cellular level [8].

Several mathematical models have been developed to explain polarization of single eukaryotic cells [9–11]. Some models rely on a local excitation, which, combined with global inhibition makes the cell respond to external gradients [12], others rely on the accumulation of a certain biochemical components to guide the motion of the single cells [13]. The accumulation responsible for this second mechanism is frequently combined with a conservation constraint because the process of polarization is fast in comparison to the production of new biochemical components. With this restriction, the mechanism of pattern formation inside living cells, together with the constraint of mass conservation, is analogous to a process of coarsening of the initial nucleus of components [14] and gives rise to phase separation [15] and to models of pattern formation [16]. Several simple models of intracellular pattern formation have appeared including the conservation restriction [13, 17, 18].

Once the axes and direction of movement are defined in amoeboid cells, small projections (defined as protrusions) are formed at the membrane of the cells [19]. These projections, which extend and retract periodically, are responsible for pushing the cell, and therefore, to move in the typical amoeboid motion. Dictyostelium discoideum is a species of soil-dwelling amoeba, frequently employed to characterize amoeboid locomotion. Inside the amoeba several signaling events are triggered, for example the activation of the Ras proteins and PI3K enzymes and accumulation of PIP₃ at the front of the cell, while activation of PTEN and myosin occur at the rear of the cell [20, 21]. Membrane areas where the protrusion activity is greater are typically characterized by the presence of Ras-GTP protein patches [22]. The appearance of Rac regions around the membrane with high protrusion activity [23, 24] has been observed in the slime mold organism Dictyostelium discoideum, where it is related to cytoskeletal dynamics [25].

A reaction-diffusion model with bistable dynamics is one of the common models of cell motility and particularly employed for Dictyostelium discoideum. Some dimensional bistable models are based on the formation of a finite lifetime and localized patches of high protein concentration [26, 27] while others are based on membrane dynamics of moving connected points [28]. Bistable conditions for cellular processes can be obtained by the coupling of a mass control regulating condition in the biochemical components present around the cytosol and the membrane of the cell, for example proteins, phospholipids and enzymes [13, 16, 29].

A common technique to model pattern formation inside a cell and the shape evolution of the membrane is the addition of a phase field with a sharp interface to distinguish the interior and exterior of the cell. This field maintains the correct boundary conditions while the borders are moving [30]. Some studies have applied phase field modeling to study keratocyte motility [31–33] and amoeboid motility [34] which can be divided into diffuse and persistent migration depending on the starvation level [35, 36]. There are also some intermediate cases observed in Dictyostelium discoideum cells for certain types of genetic variants [37] which have also been modelled with a phase field and variation of some parameters [38–40]. Other properties of Dictyostelium discoideum cells modeled employing a phase field are the viscoelasticity of the cells [41] and cell division [42]. Finally, we would like to mention that interactions among cells can also be considered for keratocyte [43, 44] and amoeboid cells [45].

Here, first, we transform a one dimensional model of the polarization at the membrane of a single Dictyostelium discoideum cell [23] into a two-dimensional domain for the waves in the basal membrane, in contact with the surface, using an additional phase field for the shape of the cell. We observe a strong dependence of the numerical dynamics on the explicit parameter values of the original model. Cell motion occurs only in a small window of parameter values, which indicates that the model is not robust to small variations of the parameters. Therefore, we propose a constraint on the conservation of a component of the signal pathway, controlling the autocatalytic mechanism, in order to increase the robustness of the model in representing changes in parameter values [46]. Similar types of conservation have previously been employed in other models of motion of Dictyostelium discoideum cells [34, 38, 47, 48], and we show here that a constraint of this kind is an useful and reasonable condition to systematically increase the robustness of the crawling mechanism, increasing the window of parameter values allowing cell migration.

2 Materials and Methods

2.1 Biochemical Model for Ras Activation and Pseudopod Extension

Biochemical components inside the Dictyostelium discoideum amoeba self-organized to follow chemical signals in the exterior by the accumulation of Ras-GTP in the front of the cell. Next, F-actin molecules accumulates also at the front triggering push of the cytoskeleton and the motion of the amoeba.

We investigate a simple reaction-diffusion model [23] for Ras-GTP (R) patches that consists on the next partial differential equation:

where we have a basal production, the stimulation production R by local occupied receptor S, an autocatalytic stimulation of R, an inhibition R by global and local inhibitors (G_R and L_R), the degradation of R, the diffusion of R and, a Gaussian spatio-temporal distributed white noise ξ_R(x, t) with zero mean ⟨ξ_R(x, t)⟩ = 0 and correlation ⟨ξ_R(x, t)ξ_R(x′, t′)⟩ = 2σ_Rδ(x − x′)δ(t − t′). The external S can significantly increase the response of Ras [23], see diagram in Figure 1, therefore, we keep here S = 0.

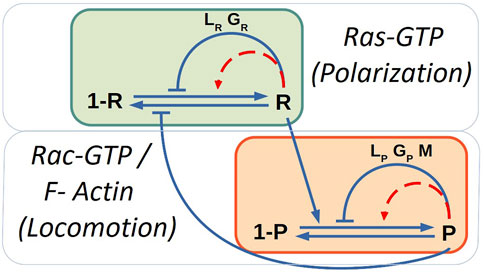
FIGURE 1. Sketch of the biochemical model of polarization due to chemotaxis and locomotion modules. Blue solid lines corresponds to the interactions and red dashed lines to auto-catalytic processes. The mass-conservation constrains control the auto-catalytic interactions.

The variables L_R and G_R correspond, respectively, to local and global inhibitors of R:

where both are produced by R and degrade, and only the local inhibitor diffuses. Note that the quantity $\bar{R}$ corresponds to the spatial average in the whole space of the field R.

At the same time we included a quantity related to the formation of protrusions (P) such as F-actin and Rac-GTP molecules; see diagram in Figure 1. This variable P was coupled with its respective inhibitors:

where we have a basal production, the stimulation production by R, an autocatalytic stimulation of P, a production by an extra term M, an inhibition of P by global and local inhibitors (G_P and L_P), the degradation of P, the diffusion of P and, a Gaussian spatio-temporal distributed white noise ξ_P(x, t) with zero mean ⟨ξ_P(x, t)⟩ = 0 and correlation ⟨ξ_P(x, t)ξ_P(x′, t′)⟩ = 2σ_Pδ(x − x′)δ(t − t′).

Similar to the previous set of equations, the variables L_P and G_P correspond, respectively, to local and global inhibitors of P:

where both are produced by P and degrade, and only the local inhibitor diffuses. Note that the quantity $\bar{P}$ corresponds to the spatial average in the whole space of the field P.

Finally, the model takes into account the inclusion of a variable of memory (M) which is coupled with P; this variable stimulates the formation of new protrusion zones and represents the results observed in some experiments:

which is produced by P, degrades and diffuses. The memory term is related to the probability of identifying when and where the signaling cascade is activated to generate new pseudopods. At a molecular level, such term is identified with the mechanisms of how information is collected, stored and used to bias future pseudopods [49, 50].

A more exhaustive description of the model is shown in the original study [23]. However, note that the noise description in the original study was different and we have adapted to an equivalent description based on physical derivations of stochastic fluctuations [51]; for more details see Supplementary Material.

One dimensional simulations were made using periodic boundary conditions in a grid of 120 points. The cell was considered as circular and having a radius of 6.25 μm. The pixel size for this case was set at Δx = 0.32 μm and the time step Δt = 0.03 s. The definition and the value of the parameters of the model can be found in Supplementary Table S1.

2.2 Physical Phase Field Model for Cell Shape Deformations

The original model did not include deformable cells. Therefore, we expanded the model to 2D geometry and introduced an auxiliary phase field ϕ with the purpose of describing the evolution of the cell shape. The use of a phase field permits a smooth variation between the values of ϕ = 1 inside and ϕ = 0 outside of the cell.

The phase field equation is the result of a force balance involving several types of forces of different origins acting in the cell body. The equation for the phase field is as follows

The first term on the right side in Eq. 8 is related to the surface energy of the cell membrane, where γ is the surface tension and G(ϕ) = 18ϕ²(1 − ϕ)² is a double well potential. The second term keeps the area close to the value of A₀. And the third term represents the active force generated by the Rac-GTP (P) molecules when pushing on the cell membrane [34]. The inclusion of the phase field permits to mimic the shape of the ventral membrane of crawling cells.

We consider a deformable cell of 122 μm² in area corresponding to a circle with radius equal to 6.25μm. The pixel size used was the half as in the 1D case Δx = Δy = 0.16 μm. Also, to increase accuracy, the time discretization was reduced to Δt = 0.003s. We integrated Eqs 1–8 using periodic boundary conditions and standard finite differences. The rest of parameters are as displayed in Supplementary Table S1.

2.3 Mathematical Description of the Mass-Conservation Constraint

The mathematical model represented in Eqs 1–7 has several conservation terms which affect the dynamics of the system; see for example Eqs.2–5. However, we further modify the original model to include a new feedback through parameters k₁₄ to create a more robust model by the control of the bistable properties, which are discussed in following sections. Therefore, the parameter k₁₄ is dynamically controlled depending on the total amount of the protein of the inducer P at the cell. A new control term related to k₁₄ is incorporated, following previous similar approaches in simple models [32, 38, 47]:

where $k_{14}^{*}$ is a new constant that take the values of the original value of k₁₄. It is important to note that the new constrain precludes the cell to be fully covered with the component P or emptying of the component P. Both extreme conditions are rare during cell crawling.

Parameter C_P is the target value of the fraction of the cell area occupied by patches of pseudopod inducer P. When, the total concentration $\bar{P}$ is larger (lower) than C_p the parameter value of k₁₄ is larger (lower) than $k_{14}^{*}$ and the bistable conditions implies the reduction (increase) of the $\bar{P}$. It corresponds to a feedback control of the parameter to keep a particular stable solution in Eq. 9. Note that for η = 0 we recover the original model.

3 Results

3.1 Mechanism of Cell Motion in the Mathematical Model Is Based in Stochastic Generation of Patches

In a one-dimensional system, mimicking the membrane of a crawling cell, the generation of a single local patch of high biochemical concentration is equivalent to cell polarization. A stable domain in a specific location of the membrane is related with actin accumulation and produces persistent motion of the cell in that direction. The random appearance and disappearance of small domains is related with amoeboid motion, where two or three pseudopods compete for a certain time. The alternation of direction gives rise to random motion of the virtual cell.

Stochastic reaction-diffusion equations, as in Eqs 1–7, and previously developed [23], can be numerically integrated into a one-dimensional domain as in the original study, where kymographs are shown for a certain window of parameter values.

If we vary the parameters k₁₄ and k₁₈, we obtain the phase diagram; see Figure 2. For large values of k₁₄ and small values of k₁₈ the membrane is completely covered by P, while for small values of k₁₄ and large values of k₁₈ the concentration of P strongly decreases. Locomotion is, therefore, expected for intermediate values of these two parameters as shown in Figure 2. For the evaluation of the mechanism of the simulations shown in Figure 2, we fixed the stochastic source of perturbations of the additive noises in Eqs 1–7 to σ_R = 0.04 and σ_P = 0.025.

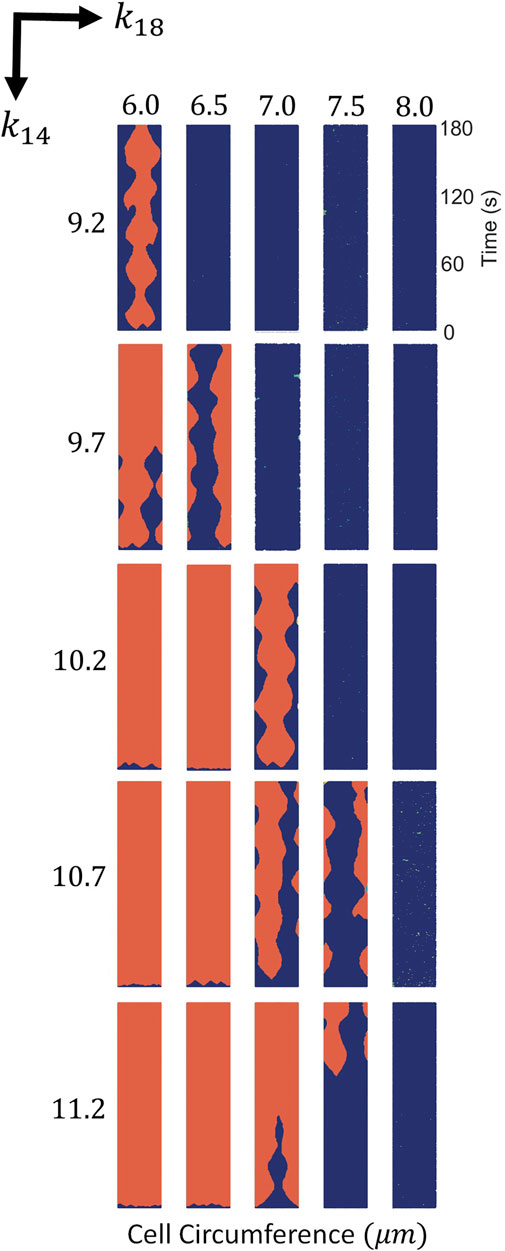
FIGURE 2. Spatio-temporal plots of P (in red) for different values of k₁₄ and k₁₈. For each panel times goes from bottom to top and horizontal direction corresponds to membrane position in the cell circumference. Variances of noise intensity were fixed at σ_R = 0.04 and σ_P = 0.025.

3.2 Mechanism of Cell Motion Is Based in Bistability

For the evaluation of the mechanism of pattern formation we found the stationary solutions for the deterministic version of Eqs 1–7 by removing the additive noise. We have slowly increased the parameter k₁₄ by small intervals (0.05 s⁻¹) and integrated the model for a considerable amount of time to permit the model reach the equilibrium (180 s). Subsequent increase of the parameter permits the observation of the evolution of the stationary value of P by obtaining a value for P in every interval in k₁₄; see Figure 3A. Once the system of equations saturated to a certain value of P $\sim 0.75-0.80$ we stopped and reduced the value of k₁₄, giving rise to a hysteresis cycle; see Figure 3A. The hysteresis cycle shows that the system actually is bistable for certain window of parameter values. Equivalent dynamics of P can be observed under a similar change in k₁₈; see Figure 3B. Therefore for low and large values of k₁₄ and k₁₈ there is a single stable solution and for intermediate values the model shows bistability.

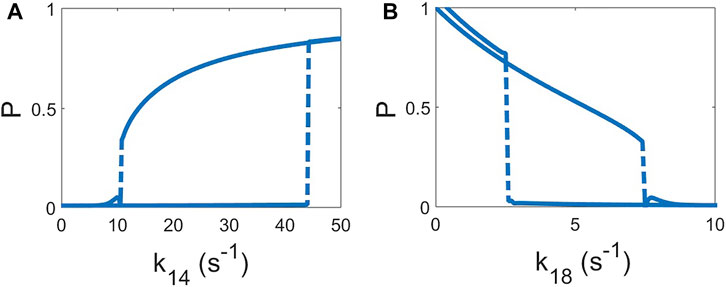
FIGURE 3. Hysteresis curves of the deterministic model (σ_R = 0 and σ_P = 0). The value of the homogeneous solution of P is shown as function of the parameter increasing and, subsequently, decreasing of k₁₄, keeping k₁₈ = 7 s⁻¹ (A) and k₁₈ keeping k₁₄ = 10.2 s⁻¹ (B). Increase and decrease of the both parameters are done by steps of 0.05 s⁻¹ and, after each step, permitting to relax to the new solution for 180 s.

It is known that the combination of a bistable dynamics with an appropriate noise intensity produces the formation of localized patches in reaction-diffusion equations [52, 53]. This formation is the mechanism responsible for the formation of localized domains of P. The localized pattern observed in Figure 2 is not due to excitable dynamics but rather to a delicate equilibrium between bistable dynamics and noise.

3.3 Stochastic Bistability Provides a Mechanism of Cell Crawling Motion in Two Dimensional Systems

For the coupling of the polarization mechanism to the cell motion we used a phase field. This additional field is employed for the definition of the interior of the cell. In this case, the two dimensional phase field permits the use of different biochemical concentrations in the ventral membrane of a crawling cell.

The extension of the stochastic reaction-diffusion described in the previous section to two dimensions permits numerical simulations of the shape of the crawling cell and the corresponding motion responding to the dynamics of the patches. In Figure 4 we showed snapshots of the in silico cells with the parameter values corresponding to the values shown in Figure 2. We reproduced the dynamics expected from the one dimensional simulations, and the crawling dynamics can be clearly studied. Again, for high values of parameter k₁₄ and small values of k₁₈ the concentration of P is mostly high and homogeneously distributed along the membrane; see Figure 4. On the other hand, in the opposite limit, for small values of k₁₄ and high values of k₁₈ the concentration of P disappears from the ventral membrane. However, for a small window of values of the parameters the cell moves and inspects the surrounding region. The shape of the resulting cell depends on the particular realization and the parameter values; in the snapshots shown in Figure 4 we obtain fan-shaped cells, a typical mode of Dictyostelium discoideum cell crawling [37].

FIGURE 4. Snapshots of the virtual cells showing P (in red) obtained from computer simulations and applying the phase field technique to the model for different values of k₁₄ and k₁₈. Variances of noise intensity were fixed at σ_R = 0.04 and σ_P = 0.025. The rest of them are consistent with Supplementary Table S1.

The dependence of locomotion on the parameters k₁₄ and k₁₈ is strong as shown in Figure 4. Persistent motion is observed only for an intermediate window of values of the two parameters. For very small or very large amounts of $\bar{P}$ cells do not move. Such quantity is determined by the parameters k₁₄ and k₁₈, and small changes on their values prevent the cell motion, making the whole model non-robust.

3.4 Noise Intensities Determine the Type of Motion

The variation of the type of cell motion is determined by the intensity of the noise. Low levels of both noises do not permit the formation of the domains of P needed to give rise to cell movement; see Figure 5. As we increase the amplitude of noise for P, we reach a single domain that fills the front part of the cell and persistent motion is shown; see middle column and right hand snapshots in Figure 5. This type of motion is reminiscent of the fan-shaped amoeboid cells previously reported [37] and also reproduced with simpler models [38]. An increase in the noise intensity produces an increase in the appearance and disappearance of pseudopods and therefore a transition to amoeboid movement; see fifth column in Figure 5 for higher noise intensities. There are some noise intensities which produce patterns and dynamics similar to the characteristic patterns observed in the experiments, however, as previously mentioned, and shown in Figure 4, small variations in the parameter values k₁₄ and k₁₈ may completely change the movement dynamics.

FIGURE 5. Map of snapshots of the virtual cell taken from different variance values of noise intensity for the original model [23]. For each column, snapshots indicate P distribution (red) inside the cell. The value of the parameter of the simulations are k₁₄ = 10.2 s⁻¹ and k₁₈ = 7 s⁻¹. The rest of them are consistent with Supplementary Table S1.

3.5 Inclusion of Mass-Conservation Constrain Qualitatively Increases Robustness

In order to reduce the high sensitivity of the appearance of motion on the parameter values, we included a conservation constraint on the total inducer P, see Eq. 9, in the biochemical rates responsible for the bistable transition in Eq. 4. Following similar previous approaches [34, 47], we included this conservation as a global feedback condition in the reaction-diffusion equations of the model, see Section 2.3.

In Figure 6, we show several realizations incorporating the conservation constraint of P proteins, for different k₁₄ and k₁₈ parameter. A direct comparison can be made with the results displayed in Figure 4 showing the effects of the inclusion of the mass conservation feedback. Results in Figure 6 show that for a wide range of parameter values, the variation of the parameters does not affect either the bistability of the model or the quantity of inducer P inside the cell phase field, which was kept constant. The inclusion of this global condition permits the use of a larger range of parameter values, increasing the robustness of the mechanism in comparison with the original model.

FIGURE 6. Map of snapshots of the virtual cell taken from different values of k₁₄ and k₁₈ for the new mass-conserved model. For each column, snapshots indicate P distribution (red) inside the cell. Variances of noise intensity were fixed at σ_R = 0.04 and σ_P = 0.025. The rest of them are consistent with Supplementary Table S1.

The shape and type of motion were affected by the noise intensity. Using the same parameters of Figure 5 we studied the effects of varying the noise variance in the new mass-conserved model. When the noise intensity related to the pseudopod inducer P increases, changes the shape from persistent fan-shape to random amoeboid phenotype, see Figure 7. This change is present because while small values of σ_P generates less blurred patches, an increment of σ_P drives the opposite effect, the appearance of more blurred and distributed patches for P.

FIGURE 7. Map of snapshots of the virtual cell taken from different variance values of noise intensity for the new mass-conserved model. For each column, snapshots indicate P distribution (red) inside the cell. The value of the parameter of the simulations are k₁₄ = 10.2 s⁻¹ and k₁₈ = 7 s⁻¹. The rest of them are consistent with Supplementary Table S1.

3.6 Inclusion of Mass-Conservation Constrain Quantitatively Increases Robustness

We measured the speed of the resulting cells for different parameter conditions for the original and the new mass-conserved models. We observed that the dynamics of the simulated cells are more robust for the mass-conserved version of the equations; see Figure 8.

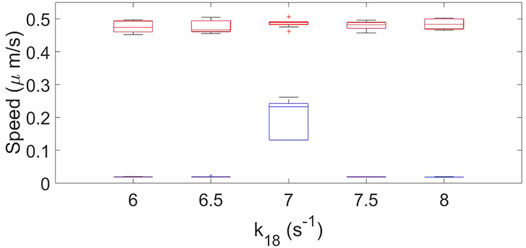
FIGURE 8. Box plot representation for the cell speed of the original model (blue color) and the new mass-conserved model (red color). Results are for when k₁₈ is varied. using a fixed value of k₁₄ = 10.2 s⁻¹, σ_R = 0.04 and σ_P = 0.025. Ten realizations for each case were performed.

For the original model the speed and shape drastically changes when varying the parameters, and only a particular combination of parameters gives rise to cell crawling (see Figure 4). On the other hand, for the new mass-conserved version both velocities and shapes are more similar to each other for a much larger window of parameter values, as we can see in the speeds calculated in Figure 8. Such results were obtained by changing k₁₈ to correspond to simulations shown in the third row of Figure 4 for the no mass conservation case and for Figure 6 for the mass-conservation system.

In Figure 9 we show the dependency of the speed on the noise σ_P for different values of σ_R. The speed of the cells employed for the calculation comes from the dynamics shown in Figures 5, 7. We observe that the speed obtained from both conditions decreases for greater noise intensities. However, for the original model almost null velocities appear for low noise magnitude. As we increase the noise intensity, values of the speed are more similar.

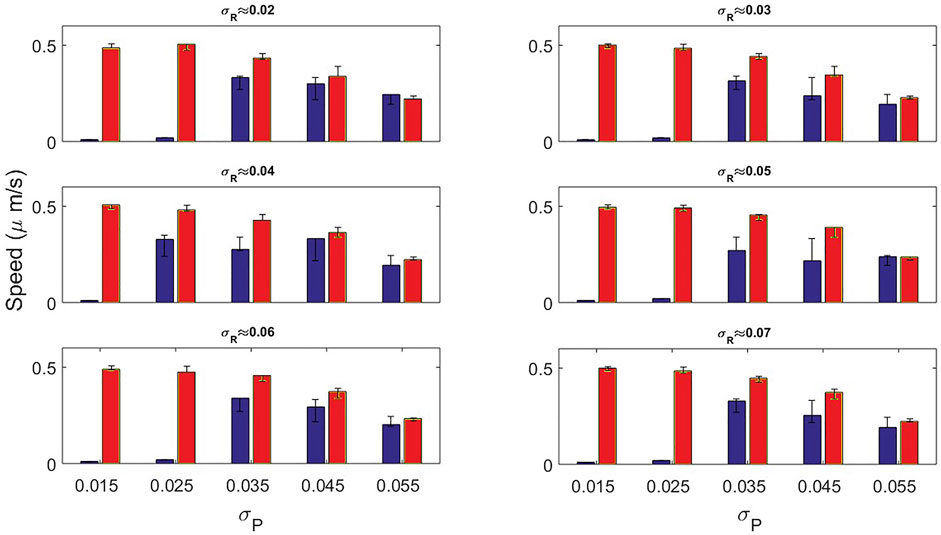
FIGURE 9. Speed bar plots measured by the original model (blue bars) and the new mass-conserved model (red bars) by varying the noise variance σ_P. In each panel the variance associated to σ_R was fixed for different values.

4 Discussion

We studied the dynamics of a one-dimensional Dictyostelium Discoideum cell model consisting in the stochastic dynamics of Ras activation (R) and pseudopod inducer (P). The deterministic version of the model reveals the emergence of bistability. This conclusion appears from the visible hysteresis transition under the change of the parameters. In contrast, the stochastic version of the model permits the transition between two stable regimes. The extension of the model into two dimensions with the use of the addition of a phase field, allowing cell deformation, shows similar dependence on the parameters, in agreement with [23].

Since for typical experimental conditions the total concentration barely changes despite environmental perturbations, we chose to incorporate global feedback for the pseudopod inducer inside the cell. Such inclusion increases the robustness of the model and expands the parameter range where cell motion is observed without affecting the shape and dynamics.

The idea behind the approach is to dynamically control the velocity of the border between the clusters of P (orange domains) and the empty region. When the size of the orange domain is above (below) a certain threshold the border contracts (expands) keeping the global size of the domain of P and therefore the polarization of the cell. Such control does not substantially depend on the rest of the parameters because it is defined to maintain the size of the domain close to a certain value, and ensures that small modifications of the parameter do not destroy the structure of the domains and the polarization. Therefore, the described mechanism is more robust that a pure parameter fitting.

A bistable dynamics together with diffusion typically produces the motion of a front in reaction-diffusion equations. Under certain fine tuned parameter values, the front velocity becomes zero [54]. If we consider such bistable variable the concentration at the membrane and we, therefore, couple its dynamics with a second variable, related with the concentration of the same protein in the cytosol, where diffusion is faster, the condition of zero velocity spontaneously appears, and the front is frozen at a particular position giving rise to wave pinning [13, 29]. Such a pinned condition appears because the coordinated balance between the membrane and the cytosol concentrations maintains constant the total amount of the protein inside the cell. Therefore, some other new models consider only a single variable for the membrane together with a global feedback to account for the mass-conservation condition for a single concentration [17, 32, 38]. When the dynamics of the concentration at the membrane is combined with other membrane concentrations more complex models including also excitable signalling networks are developed [39, 47, 48, 55]. In contrast with such models, in this study we chose an existing complex model where the condition of bistability is finely tuned [23] and add the global feedback condition to account for the conservation of the protein. Such modification highly increases the robustness of the model and, therefore, its applicability to other conditions.

Two of the parameters k₁₄ and k₁₈ can show hysteresis loops in the concentration of P, see Figure 3. We have employed the global feedback in the condition of parameter k₁₄, see Eq. 9, however we could have employed a similar condition for parameter k₁₈ or any other parameter which exhibits a hysteresis behavior on the concentration P. Actually, note that other global feedback were already considered in the original version of the model [23]; see the dynamics of the global inhibitors, defined by G_R and G_P in Eqs 2–5 respectively, similarly to other models of the motion of Dictyostelium discoideum cells based on global cytosolic quantities [12, 48]. The addition of global control quantities which can determine the available concentration inside the cell has previously been employed in other models [32, 38, 47].

Instant speed was measured, highlighting that for the original model a considerable set of parameters driven to velocities of close to zero, while for the set of parameters for the new mass-conserved model the speed remained almost constant around 0.45 μm/s.

Note that we have shown that the original model is based on a bistable conditions with the appropriate noise intensity. We have previously used simple stochastic bistable models for the description of the motion of Dictyostelium discoideum cells [34, 38] based on the same concept together with a mass-conservation constraint. There are also other models based on similar constraints [24, 40, 47] where some of the key differences relies in the inherent oscillatory dynamics of the models, the specific parameters that need to be change to generate different types of cell motion (e.g., amoeboid or keratocyte) without affecting the biochemical signaling dynamics; apart from the number of membrane concentrations involved in the cell dynamics as already mentioned. Therefore, the addition of a mass conservation constraint is a convenient mechanism to increase robustness in the delicate equilibrium between stochastic fluctuations and a bistable condition.

The coupling of the Ras activation R on the pseudopod inducer P is weak. The coupling is produced by the term proportional to k₁₃ and it increases the probability of the generation of patches of P. A chemotactic concentration can enhance R and, therefore, polarize the field P and direct the locomotion [23]. In the absence of chemotaxis the coupling is small, while more physiological conditions may require larger couplings. In Figure 10 we increased parameter k₁₃ to demonstrate the increase in the coupling of both field R and P through the parameter. Intermediate values can be compared with experimental measures to fit an appropriate value; however such evaluation is outside the scope of this work.

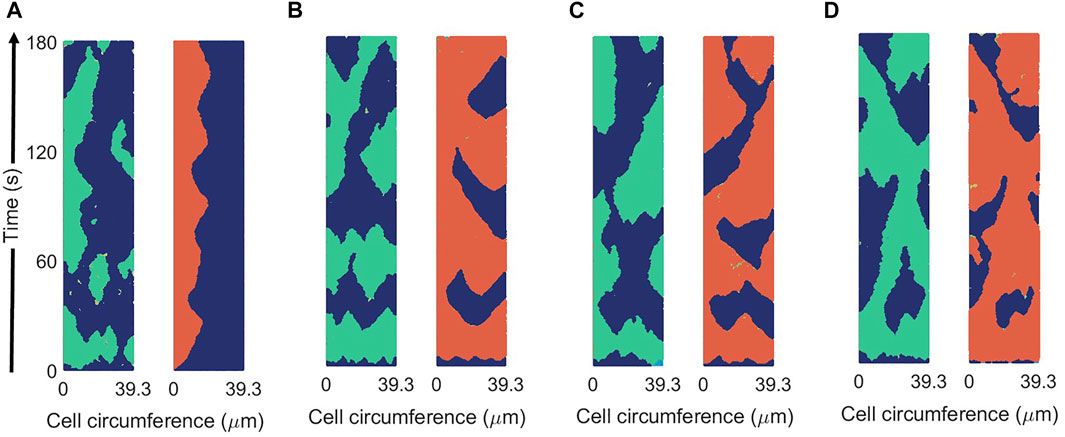
FIGURE 10. Spatio-temporal plots of R (in green) and P (in red) for different values of the coupling parameter between R and P: k₁₃ = 0.1 s⁻¹ (A), k₁₃ = 0.5 s⁻¹ (B), k₁₃ = 1 s⁻¹ (C), and k₁₃ = 2 s⁻¹ (D) in the new mass-conserved model. Results are for a fixed values of σ_R = 0.04 and σ_P = 0.025.

An extension of the new mass-conserved model is possible with the inclusion of an external chemo-attractant gradient to analyze the response, known as chemotaxis and already considered in the original model [23]. Future simulations should study the relation of the chemotactic motion of Dictyostelium discoideum cells with the stochastic fluctuations and the rest of the parameters. They should also measure the effects on the shape and speed caused by the gradient.

In summary, we have shown that the inclusion of a mass-conservation constraint in the correct position substantially increases the robustness of a computational model of a crawling cell.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

EM performed the numerical simulations; EM and SA contributed to the design and implementation of the research, to the analysis of the results and to the writing of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank grant PGC2018-095456-B-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe,” by the “European Union.” E.M. acknowledges also financial support from CONACYT.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.881885/full#supplementary-material

References