Stability Analysis of Stagnation-Point Flow in a Nanofluid over a Stretching/Shrinking Sheet with Second-Order Slip, Soret and Dufour Effects: A Revised Model
Abstract
:1. Introduction
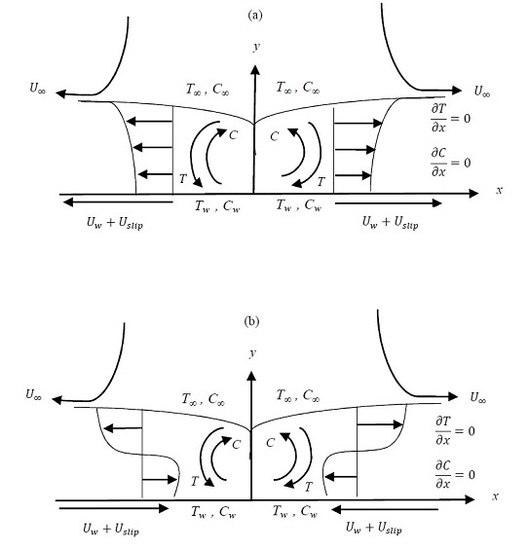
2. Basic Equations
3. Steady-State Solution
4. Stability Analysis
5. Results and Discussion
6. Conclusions
- The skin friction coefficient decreased as the first-order slip parameter and the magnitude of the second-order slip parameter ( and ) increased, whereas the heat transfer rate increased.
- The range of solutions widely expanded with the increment of the first-order slip parameter, while the expansion of the range of solutions was very small when the second-order slip parameter was considered.
- The smallest Soret number was required to increase the heat transfer rate at the surface.
- The heat transfer rate at the surface increased rapidly as the Brownian motion parameter decreased, while the largest value of was required to increase the mass transfer rate at the surface.
- The largest value of the thermophoresis parameter was required to increase the heat transfer rate, while, for the mass transfer rate, the smallest value of was needed.
- The first solution was a stable solution and, hence, its physical properties could be realized, whereas the second solution was an unstable solution and, hence, not physically realizable.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Masuda, H.; Ebata, A.; Teramee, K.; Hishinuma, N. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Netsu Bessei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Haq, R.U.; Khan, Z.H.; Khan, W.A. Thermophysical effects of carbon nanotubes on MHD flow over a stretching surface. Phys. E Low Dimens. Syst. Nanostruct. 2014, 63, 215–222. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary-layer flow of nanofluids over a moving surface in a flowing fluid. Int. J. Therm. Sci. 2010, 49, 1663–1668. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Pop, I.; Asghar, S.; Obaidat, S. Stagnation-point flow of a nanofluid towards a stretching sheet. Int. J. Heat Mass Transf. 2011, 54, 5588–5594. [Google Scholar] [CrossRef]
- Hamid, R.; Nazar, R.; Pop, I. Non-alignment stagnation-point flow of a nanofluid past a permeable stretching/shriking sheet: Buongiorno’s model. Sci. Rep. 2015, 5, 14640. [Google Scholar] [CrossRef] [PubMed]
- Mansur, S.; Ishak, A.; Pop, I. The magnetohydrodynamic stagnation point flow of a nanofluid over s tretching/shrinking sheet with suction. PLoS ONE 2015, 10, e0117733. [Google Scholar] [CrossRef] [PubMed]
- Jamaludin, A.; Nazar, R.; Pop, I. Three-dimensional mixed convection stagnation point flow over a permeable vertical stretching/shrinking surface with a velocity slip. Chin. J. Phys. 2017, 55, 1865–1882. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. The Cheng-Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid: A revised model. Int. J. Heat Mass Transf. 2013, 65, 682–685. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary layer flow of a nanofluid past a vertical plate: A revised model. Int. J. Therm. Sci. 2014, 77, 126–129. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A.; Pop, I. Flow past a permeable stretching/shrinking sheet in a nanofluid using two-phase model. PLoS ONE 2014, 9, e111743. [Google Scholar] [CrossRef] [PubMed]
- Esfe, M.H.; Arani, A.A.A.; Karimipour, A.; Sadegh, S.; Esforjani, M. Numerical simulation of natural convection around an obstacle placed in an enclosure filled with different types of nanofluids. Heat Transf. Res. 2014, 45, 279–292. [Google Scholar]
- Karimipour, A.; Esfe, M.H.; Safaei, M.R.; Semiromi, D.T.; Jafari, S.; Kazi, S.N. Mixed convection of copper–water nanofluid in a shallow inclined lid driven cavity using the lattice Boltzmann method. Phys. A 2014, 402, 150–168. [Google Scholar] [CrossRef]
- Karimipour, A.; Nezhad, A.H.; D’Orazio, A.; Esfe, M.H.; Safaei, M.R.; Shirani, E. Simulation of copper–water nanofluid in a microchannel in slip flow regime using the lattice Boltzmann method. Eur. J. Mech. B Fluids 2015, 49, 89–99. [Google Scholar] [CrossRef]
- Karimipour, A. New correlation for Nusselt number of nanofluid with Ag/Al2O3/Cu nanoparticles in a microchannel considering slip velocity and temperature jump by using lattice Boltzmann method. Int. J. Therm. Sci. 2015, 91, 146–156. [Google Scholar] [CrossRef]
- Esfe, M.H.; Yan, W.M.; Akbari, M.; Karimipour, A.; Hassani, M. Experimental study on thermal conductivity of DWCNT-ZnO/water-EG nanofluids. Int. Commun. Heat Mass Transf. 2015, 68, 248–251. [Google Scholar] [CrossRef]
- Gal-el-Hak, M. The fluid mechanics of micro-devices the Freeman scholar lecture. Trans. ASME J. Fluids Eng. 1999, 121, 5–23. [Google Scholar] [CrossRef]
- Shidlovskiy, V.P. Introduction to the Dynamics of Rarefied Gases; American Elsevier Publishing Company Inc.: New York, NY, USA, 1967. [Google Scholar]
- Pande, G.C.; Goudas, C.L. Hydromagnetic Rayleigh problem for a porous wall in slip regime. Astrophys. Space Sci. 1996, 243, 285–289. [Google Scholar] [CrossRef]
- Wu, L. A slip model for rarefied gas flows at arbitrary Knudsen number. Appl. Phys. Lett. 2008, 93, 253103. [Google Scholar] [CrossRef]
- Fang, T.; Yao, S.; Zhang, J.; Aziz, A. Viscous flow over a shrinking sheet with a second-order slip flow model. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 1831–1842. [Google Scholar] [CrossRef]
- Fang, T.; Aziz, A. Viscous flow with second-order slip velocity over a stretching sheet. Z. Naturforsch. A 2010, 65, 1087–1092. [Google Scholar] [CrossRef]
- Nandeppanavar, M.M.; Vajravelu, K.; Abel, M.S.; Siddalingappa, M.N. Second order slip flow and heat transfer over a stretching sheet with non-linear Navier boundary condition. Int. J. Therm. Sci. 2012, 58, 143–150. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. Boundary layer flow and heat transfer past a permeable shrinking surface embedded in a porous medium with a second-order slip: A stability analysis. Appl. Therm. Eng. 2016, 115, 1407–1411. [Google Scholar] [CrossRef]
- Singh, G.; Chamkha, A.J. Dual solutions for second-order slip flow and heat transfer on a vertical permeable shrinking sheet. Ain Shams Eng. J. 2013, 4, 911–917. [Google Scholar] [CrossRef]
- Khaderm, M.M. Laguerre collocation method for the flow and heat transfer due to a permeable stretching surface embedded in a porous medium with a second order slip and viscous dissipation. Appl. Math. Comput. 2014, 243, 503–513. [Google Scholar]
- Hakeem, A.K.A.; Ganesh, N.V.; Ganga, B. Magnetic field effect on second order slip flow of nanofluid over a stretching.shrinking sheet with thermal radiation effect. J. Magn. Magn. Mater. 2015, 381, 243–257. [Google Scholar] [CrossRef]
- Soid, S.K.; Kechil, S.A.; Ishak, A. Axisymmetric stagnation-point flow over a stretching/shrinking plate with second-order velocity slip. Propuls. Power Res. 2016, 5, 194–201. [Google Scholar] [CrossRef]
- Platten, J.K. The Soret effect: A review of recent experimental results. J. Appl. Mech. 2006, 73, 5–15. [Google Scholar] [CrossRef]
- Eslamian, M. Advances in thermodiffusion and thermophoresis (Soret effect) in liquid mixtures. Front. Heat Mass Transf. 2011, 2, 20. [Google Scholar] [CrossRef]
- Kafoussisas, N.G.; Williams, E.W. Thermal-diffusion and diffusion-thermo effects on mixed free-forced convective and mass transfer boundary layer flow with temperature dependent viscosity. Int. J. Eng. Sci. 1995, 33, 1369–1384. [Google Scholar] [CrossRef]
- Eldabe, N.T.; El-Saka, A.G.; Fouad, A. Thermal-diffusion and diffusion-thermo effects on mixed free-forced convective and mass transfer boundary layer flow for non-Newtonian fluid with temperature dependent viscosity. Appl. Math Comp. 2004, 152, 867–883. [Google Scholar]
- Bhattacharyya, K.; Layek, G.C.; Seth, G.S. Soret and Dufour effects on convective heat and mass transfer in stagnation-point flow towards a shrinking surface. Phys. Scr. 2014, 89, 095203. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Bhuvaneswari, M.; Sivasankaran, S.; Rajan, S. Soret and Dufour effects on MHD mixed convection heat and mass transfer of a stagnation point flow towards a vertical plate in a porous medium with chemical reaction, radiation and heat generation. J. Appl. Fluid Mech. 2016, 9, 1447–1455. [Google Scholar] [CrossRef]
- Reddy, P.S.; Rao, D.R.V.P. Combined influence of Soret and Dufour effects on convective heat and mass transfer flow through a porous medium in cylindrical annulus with heat sources. Afr. J. Math. Comp. Sci. Res. 2010, 3, 237–254. [Google Scholar]
- Sharma, B.K.; Yadav, K.; Mishra, N.K.; Chaudhary, R.C. Soret and Dufour effects on unsteady MHD mixed convection flow past a radiative vertical porous plate embedded in a porous medium with chemical reaction. Appl. Math. 2012, 3, 717–723. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Mallikarjuna, B.; Bhuvanavijaya, R. Soret and Dufour effects on mixed convection along a vertical wavy surface in a porous medium with variable properties. Ain Shams Eng. J. 2015, 6, 553–564. [Google Scholar] [CrossRef]
- Dzulkifli, N.F.; Bachok, N.; Pop, I.; Yacob, N.A.; Arifin, N.M.; Rosali, H. Soret and Dufour effects on unsteady boundary layer flow and heat transfer of nanofluid over a stretching/shrinking sheet: A stability analysis. J. Chem. Eng. Process Technol. 2017, 8, 1000336. [Google Scholar] [CrossRef]
- Merkin, J.H. On Dual Solutions Occuring in Mixed Conve-ction in a Porous Medium. J. Eng. Math. 1985, 20, 171–179. [Google Scholar] [CrossRef]
- Merill, K.; Beauchesne, M.; Previte, J.; Paullet, J.; Weidman, P. Final steady flow near a stagnation point on a vertical surface in a porous medium. Int. J. Heat Mass Transf. 2006, 49, 4681–4686. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K. Stability analysis of dual solutions in stagnation-point flow and heat transfer over a power-law shrinking surface. Int. J. Nonlinear Sci. 2011, 12, 86–94. [Google Scholar]
- Noor, A.; Nazar, R.; Jafar, K. Stability analysis of stagnation-point flow past a shrinking sheet in a nanofluid. J. Qual. Meas. Anal. 2014, 10, 51–63. [Google Scholar]
- Nazar, R.; Noor, A.; Jafar, K.; Pop, I. Stability analysis of three-dimensional flow and heat transfer over a permeable shrinking surface in a Cu-water nanofluid. Int. J. Math. Comp. Phys. Electr. Comp. Eng. 2014, 8, 782–788. [Google Scholar]
- Jusoh, R.; Nazar, R. Stagnation point flow and heat transfer of a nanofluid over a stretching/shrinking sheet with convective boundary conditions and suction. AIP Conf. Proc. 2017, 1830, 020043. [Google Scholar] [CrossRef]
- Hafidzuddin, E.H.; Nazar, R.; Arifin, N.M.; Pop, I. Stability analysis of unsteady three-dimensional viscous flow over a permeable stretching/shrinking surface. J. Qual. Meas. Anal. 2015, 11, 19–31. [Google Scholar]
- Ishak, A. Flow and heat transfer over a shrinking sheet: A stability analysis. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2014, 8, 905–909. [Google Scholar]
- Ismail, N.S.; Arifin, N.M.; Bachok, N.; Mahiddin, N. Stagnation-point flow and heat transfer over an exponentially shrinking sheet: A stability analysis. AIP Conf. Proc. 2016, 1739, 020023. [Google Scholar]
- Najib, N.; Bachok, N.; Arifin, N.M.; Senu, N. Boundary layer flow and heat transfer of nanofluids over a moving plate with partial slip and thermal convective boundary condition: Stability analysis. Int. J. Mech. 2017, 11, 19–24. [Google Scholar]
- Najib, N.; Bachok, N.; Arifin, N.M. Stability of dual solutions of mass transfer on a continuous flat plate moving in parallel or reversely to a free stream in the presence of a chemical reaction with second order slip. AIP Conf. Proc. 2017, 1830, 020009. [Google Scholar]
- Bachok, N.; Najib, N.; Arifin, N.M.; Senu, N. Stability of dual solutions in boundary layer flow and heat transfer on a moving plate in a copper-water nanofluid with slip effect. WSEAS Trans. Fluid Mech. 2016, 11, 151–158. [Google Scholar]
- Noor, M.A.M.; Nazar, R.; Jafar, K.; Pop, I. Stability analysis of flow and heat transfer on a permeable moving plate in a Co-flowing nanofluid. AIP Conf. Proc. 2014, 1614, 898–905. [Google Scholar]
- Mukhopadhyay, S.; Andersson, H.I. Effects of slip and heat transfer analysis of flow over an unsteady stretching surface. Heat Mass Transf. 2009, 45, 1447–1452. [Google Scholar] [CrossRef]
- Roşca, A.V.; Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transf. 2013, 60, 355–364. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B.; Nandeppanavar, M.M. MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet. Int. J. Heat Mass Transf. 2013, 56, 1–9. [Google Scholar] [CrossRef]










| σ | δ | ε | First Solution | Second Solution |
|---|---|---|---|---|
| 0.1 | −0.1 | −1.257 | 0.0722 | −0.0714 |
| −1.25 | 0.2492 | −0.2397 | ||
| −1.2 | 0.6975 | −0.6230 | ||
| 0.5 | −0.5 | −1.716 | 0.0295 | −0.0295 |
| −1.71 | 0.1671 | −0.1659 | ||
| −1.7 | 0.2706 | −0.2676 | ||
| 1 | −1 | −2.75 | 0.0489 | −0.0488 |
| −2.7 | 0.3561 | −0.3531 | ||
| −2.6 | 0.6139 | −0.6048 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najib, N.; Bachok, N.; Arifin, N.M.; Ali, F.M. Stability Analysis of Stagnation-Point Flow in a Nanofluid over a Stretching/Shrinking Sheet with Second-Order Slip, Soret and Dufour Effects: A Revised Model. Appl. Sci. 2018, 8, 642. https://0-doi-org.brum.beds.ac.uk/10.3390/app8040642
Najib N, Bachok N, Arifin NM, Ali FM. Stability Analysis of Stagnation-Point Flow in a Nanofluid over a Stretching/Shrinking Sheet with Second-Order Slip, Soret and Dufour Effects: A Revised Model. Applied Sciences. 2018; 8(4):642. https://0-doi-org.brum.beds.ac.uk/10.3390/app8040642
Chicago/Turabian StyleNajib, Najwa, Norfifah Bachok, Norihan Md Arifin, and Fadzilah Md Ali. 2018. "Stability Analysis of Stagnation-Point Flow in a Nanofluid over a Stretching/Shrinking Sheet with Second-Order Slip, Soret and Dufour Effects: A Revised Model" Applied Sciences 8, no. 4: 642. https://0-doi-org.brum.beds.ac.uk/10.3390/app8040642