Airfield Infrastructure Management Using Network-Level Optimization and Stochastic Duration Modeling
Abstract
:1. Introduction
2. Background
3. Methodology
3.1. Pavement Condition Forecast with Stochastic Duration Models
3.2. Network Optimization-Based Framework for M&R Planning
3.2.1. Basic Idea
3.2.2. Model Formulation
3.2.3. Obtaining Facility-Specific M&R Recommendations over a Planning Horizon
4. Application at Chicago O’Hare Airport
4.1. Estimation Results of the Stochastic Duration Models
4.2. Computation of Condition State Transition Probabilities
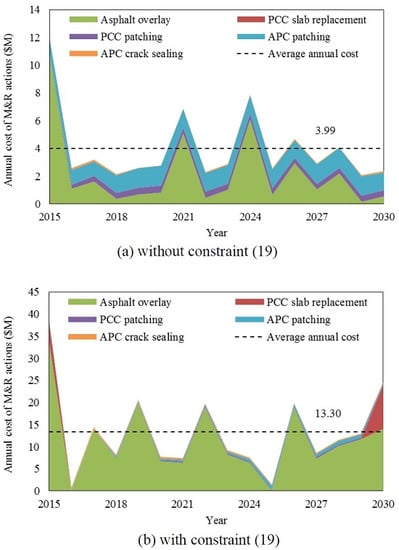
4.3. M&R Plan for the 2015–2030 Period
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Airport Improvement Program (AIP) Grant Data. Available online: https://www.faa.gov/airports/aip/grantapportion_data/ (accessed on 1 November 2018).
- Gendreau, M.; Soriano, P. Airport pavement management systems: An appraisal of existing methodologies. Transp. Res. Part A.: Policy Pract. 1998, 32, 197–214. [Google Scholar] [CrossRef]
- Shahin, M.Y. Pavement Management for Airports, Roads, and Parking Lots; Springer: New York, NY, USA, 2005. [Google Scholar]
- ACRP Common Airport Pavement Maintenance Practices: A Synthesis of Airport Practice. Available online: http://dot.ca.gov/hq/planning/aeronaut/documents/acrp/acrp_syn_022.pdf (accessed on 1 November 2018).
- Mishalani, R.G.; Madanat, S. Computation of infrastructure transition probabilities using stochastic duration models. J. Infrastruct. Syst. 2002, 8, 139–148. [Google Scholar] [CrossRef]
- Kuhn, K.D.; Madanat, S. Model uncertainty and the management of a system of infrastructure facilities. Transp. Res. Part C Emerg. Technol. 2005, 13, 391–404. [Google Scholar] [CrossRef] [Green Version]
- Madanat, S.; Bulusu, S.; Mahmoud, A. Estimation of infrastructure distress initiation and progression models. J. Infrastruct. Syst. 1995, 1, 146–150. [Google Scholar] [CrossRef]
- Madanat, S.; Wan Hashim, W.I. Poisson regression models of infrastructure transition probabilities. J. Transp. Eng. 1995, 121, 267–272. [Google Scholar] [CrossRef]
- Guillaumot, V.M.; Durango, P.L.; Madanat, S. Adaptive optimization of infrastructure maintenance and inspection decisions under performance model uncertainty. J. Infrastruct. Syst. 2003, 9, 133–139. [Google Scholar] [CrossRef]
- Golabi, K.; Kulkarni, R.B.; Way, G.B. A statewide pavement management system. Interfaces 1982, 12, 5–21. [Google Scholar] [CrossRef]
- Smilowitz, K.; Madanat, S. Optimal inspection and maintenance policies for infrastructure networks. Comput.-Aided Civ. Infrastruct. Eng. 2000, 15, 5–13. [Google Scholar] [CrossRef]
- Yeo, H.; Yoon, Y.; Madanat, S. Algorithms for bottom-up maintenance optimisation for heterogeneous infrastructure systems. Struct. Infrastruct. Eng. 2013, 9, 317–328. [Google Scholar] [CrossRef]
- Furuya, A.; Madanat, S. Accounting for network effects in railway asset management. J. Transp. Eng. 2013, 139, 92–100. [Google Scholar] [CrossRef]
- Camahan, J.V.; Davis, W.J.; Shahin, M.Y.; Keane, P.L.; Wu, M.I. Optimal maintenance decisions for pavement management. J. Transp. Eng. 1987, 113, 554–572. [Google Scholar] [CrossRef]
- Carnahan, J.V. Analytical framework for optimizing pavement maintenance. J. Transp. Eng. 1988, 114, 307–322. [Google Scholar] [CrossRef]
- Feighan, K.; Shahin, M.; Sinha, K.; White, T. Application of dynamic programming and other mathematical techniques to pavement management systems. Transp. Res. Rec. J. Transp. Res. Board 1988, 1200, 90–98. [Google Scholar]
- Harper, W.; Lam, J.; al-Salloum, A.; al-Sayyari, S.; al-Theneyan, S.; Ilves, G.; Majidzadeh, K. Stochastic optimization subsystem of a network-level bridge management system. Transp. Res. Rec. J. Transp. Res. Board 1990, 1268, 68–74. [Google Scholar]
- Gopal, S.; Majidzadeh, K. Application of Markov decision process to level-of-service-based maintenance systems. Transp. Res. Rec. J. Transp. Res. Board 1991, 1304, 12–18. [Google Scholar]
- Mayet, J.; Madanat, S. Incorporation of seismic considerations in bridge management systems. Comput.-Aided Civ. Infrastruct. Eng. 2002, 17, 185–193. [Google Scholar] [CrossRef]
- Lee, J.; Madanat, S. Jointly optimal policies for pavement maintenance, resurfacing and reconstruction. EURO J. Transp. Logist. 2015, 4, 75–95. [Google Scholar] [CrossRef]
- Durango, P.L.; Sarutipand, P. Capturing interdependencies and heterogeneity in the management of multifacility transportation infrastructure systems. J. Infrastruct. Syst. 2007, 13, 115–123. [Google Scholar] [CrossRef]
- Ouyang, Y. Pavement resurfacing planning for highway networks: Parametric policy iteration approach. J. Infrastruct. Syst. 2007, 13, 65–71. [Google Scholar] [CrossRef]
- Zou, B.; Madanat, S. Incorporating delay effects into airport runway pavement management systems. J. Infrastruct. Syst. 2012, 18, 183–193. [Google Scholar] [CrossRef]
- Robelin, C.; Madanat, S. Reliability-based system-level optimization of bridge maintenance and replacement decisions. Transp. Sci. 2008, 42, 508–513. [Google Scholar] [CrossRef]
- Chan, W.T.; Fwa, T.F.; Tan, C.Y. Road-maintenance planning using genetic algorithms I: Formulation. J. Transp. Eng. 1994, 120, 693–709. [Google Scholar] [CrossRef]
- Ng, M.; Lin, D.Y.; Waller, S.T. Optimal long-term infrastructure maintenance planning accounting for traffic dynamics. Comput.-Aided Civ. Infrastruct. Eng. 2009, 24, 459–469. [Google Scholar] [CrossRef]
- Medury, A.; Madanat, S. Simultaneous network optimization approach for pavement management systems. J. Infrastruct. Syst. 2013, 20, 04014010. [Google Scholar] [CrossRef]
- Nazari, F.; Noruzoliaee, M.; Zou, B.; Mohammadian, A. Optimal facility-specific inspection and maintenance decisions under measurement uncertainty: Unifying framework. J. Infrastruct. Syst. 2017, 23, 04017036. [Google Scholar] [CrossRef]
- Chan, P.; Oppermann, M.; Wu, S. North Carolina’s experience in development of pavement performance prediction and modeling. Transp. Res. Rec. J. Transp. Res. Board 1997, 1592, 80–88. [Google Scholar] [CrossRef]
- Jiang, Y.; Saito, M.; Sinha, K. Bridge performance prediction model using the Markov chain. Transp. Res. Rec. J. Transp. Res. Board 1988, 1180, 25–32. [Google Scholar]
- Ortiz-García, J.J.; Costello, S.B.; Snaith, M.S. Derivation of transition probability matrices for pavement deterioration modeling. J. Transp. Eng. 2006, 132, 141–161. [Google Scholar]
- Madanat, S.; Mishalani, R.; Wan Hashim, W.I. Estimation of infrastructure transition probabilities from condition rating data. J. Infrastruct. Syst. 1995, 1, 120–125. [Google Scholar] [CrossRef]
- Madanat, S.; Karlaftis, M.G.; McCarthy, P.S. Probabilistic infrastructure deterioration models with panel data. J. Infrastruct. Syst. 1997, 3, 4–9. [Google Scholar] [CrossRef]
- Anastasopoulos, P.C.; Labi, S.; Karlaftis, M.G.; Mannering, F.L. Exploratory state-level empirical assessment of pavement performance. J. Infrastruct. Syst. 2011, 17, 200–215. [Google Scholar] [CrossRef]
- Prozzi, J.A.; Madanat, S. Using duration models to analyze experimental pavement failure data. Transp. Res. Rec. J. Transp. Res. Board 2000, 1699, 87–94. [Google Scholar] [CrossRef]
- Mauch, M.; Madanat, S. Semiparametric hazard rate models of reinforced concrete bridge deck deterioration. J. Infrastruct. Syst. 2001, 7, 49–57. [Google Scholar] [CrossRef]
- Nakat, Z.S.; Madanat, S. Stochastic duration modeling of pavement overlay crack initiation. J. Infrastruct. Syst. 2008, 14, 185–192. [Google Scholar]
- Hong, F.; Prozzi, J.A. Estimation of pavement performance deterioration using Bayesian approach. J. Infrastruct. Syst. 2006, 12, 77–86. [Google Scholar] [CrossRef]
- Straub, D. Stochastic modeling of deterioration processes through dynamic Bayesian networks. J. Eng. Mech. 2009, 135, 1089–1099. [Google Scholar]
- Walgama, N.K.; Zhang, T.; Dwight, R. Calibrating Markov chain–based deterioration models for predicting future conditions of railway bridge elements. J. Bridge Eng. 2015, 20, 04014060. [Google Scholar]
- Roberts, C.A.; Attoh-Okine, N.O. A Comparative analysis of two artificial neural networks using pavement performance prediction. Comput.-Aided Civ. Infrastruct. Eng. 1998, 13, 339–348. [Google Scholar] [CrossRef]
- Bianchini, A.; Bandini, P. Prediction of pavement performance through neuro-fuzzy reasoning. Comput.-Aided Civ. Infrastruct. Eng. 2010, 25, 39–54. [Google Scholar] [CrossRef]
- Butler, B.; Carmichael, R., III; Flanagan, P. Impact of Pavement Maintenance on Damage Rate; Federal Highway Administration: Washington, DC, USA, 1985. [Google Scholar]
- Madanat, S.; Mishalani, R. Selectivity bias in modeling highway pavement maintenance effectiveness. J. Infrastruct. Syst. 1998, 4, 134–137. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Ramaswamy, R. An approach for predicting latent infrastructure facility deterioration. Transp. Sci. 1993, 27, 174–193. [Google Scholar] [CrossRef]
- Mohamad, D.; Sinha, K.; McCarthy, P. Relationship between pavement performance and routine maintenance: Mixed Logit approach. Transp. Res. Rec. J. Transp. Res. Board 1997, 1597, 16–21. [Google Scholar] [CrossRef]
- Chu, C.; Durango-Cohen, P.L. Incorporating maintenance effectiveness in the estimation of dynamic infrastructure performance models. Comput.-Aided Civ. Infrastruct. Eng. 2008, 23, 174–188. [Google Scholar] [CrossRef]
- Chu, C.; Durango-Cohen, P.L. Estimation of dynamic performance models for transportation infrastructure using panel data. Transp. Res. Part B 2008, 42, 57–81. [Google Scholar] [CrossRef]
- Chu, J.C. Condition-dependent maintenance effectiveness in dynamic performance models for transportation infrastructure. J. Infrastruct. Syst. 2013, 19, 85–98. [Google Scholar] [CrossRef]
- Greene, W. Econometric Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 2012. [Google Scholar]
- Ouyang, Y.; Madanat, S. An analytical solution for the finite-horizon pavement resurfacing planning problem. Transp. Res. Part B 2006, 40, 767–778. [Google Scholar] [CrossRef]
- Ouyang, Y.; Madanat, S. Optimal scheduling of rehabilitation activities for multiple pavement facilities: Exact and approximate solutions. Transp. Res. Part A Policy Pract. 2004, 38, 347–365. [Google Scholar] [CrossRef]
- Gu, W.; Ouyang, Y.; Madanat, S. Joint optimization of pavement maintenance and resurfacing planning. Transp. Res. Part B 2012, 46, 511–519. [Google Scholar] [CrossRef]
- Medury, A.; Madanat, S. Incorporating network considerations into pavement management systems: A case for approximate dynamic programming. Transp. Res. Part C Emerg. Technol. 2013, 33, 134–150. [Google Scholar] [CrossRef]
- Rubinstein, R.; Kroese, D. Simulation and the Monte Carlo Method; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Schwartz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Chicago Department of Aviation. 10-Year Capital Improvement Program (CIP) 2012–2021; Chicago Department of Aviation: Chicago, IL, USA, 2011.




| Sets | |
| M&R actions including the “do-nothing” alternative | |
| condition states | |
| runways | |
| pavement facilities | |
| cross-sectional locations of facilities ( {keel, outband}) | |
| pavement age in a condition state (age-in-state) | |
| Variables | |
| 1 if action is selected for facility during year ; 0 otherwise | |
| fraction of facilities on runway that are located on cross-section , paved with material , and in condition state for years, to which action is applied during year | |
| Parameters | |
| condition state of facility at the beginning of year | |
| material type of facility at the beginning of year | |
| age-in-state of facility at the beginning of year | |
| annual budget in year | |
| unit cost of implementing action when a facility is in state | |
| area of facility | |
| area of runway | |
| maximum acceptable fraction of facilities on each runway in condition state | |
| transition probability from state to of facilities located on cross-section , paved with material , and with age-in-state if action is applied | |
| binary indicator of material change, equal to 1 if action replaces material with material ; 0 otherwise | |
| binary indicator of age-in-state change, equal to 1 in either of two situations: (1) a state transition from to () with action a and age-in-state changes from to ; (2) no state transition (): age-in-state changes from to either with a minor action or with a major action ; 0 otherwise | |
| 1 if facility is located on runway ; 0 otherwise | |
| 1 if facility is located on cross-section ; 0 otherwise | |
| 1 if action is not compatible with material ; 0 otherwise |
| Runway Code | Area (000 sq. meters) | No. of Facilities | Surface (% area) | Condition (% area) | |||
|---|---|---|---|---|---|---|---|
| PCC * | APC ** | State 1 | State 2 | State 3 | |||
| R9R | 113.7 | 28 | 21.76 | 78.24 | 41.31 | 58.69 | 0 |
| R9L | 104.5 | 9 | 100 | 0 | 100 | 0 | 0 |
| R4R | 112.5 | 9 | 0 | 100 | 100 | 0 | 0 |
| R4L | 99.2 | 34 | 0 | 100 | 87.97 | 11.55 | 0.48 |
| R14R | 180.9 | 24 | 0 | 100 | 90.46 | 9.54 | 0 |
| R10L | 182.1 | 21 | 29.67 | 70.33 | 59.66 | 40.34 | 0 |
| R10C | 186.8 | 19 | 100 | 0 | 100 | 0 | 0 |
| sum | 979.7 | 144 | 37.77 | 62.23 | 82.71 | 17.24 | 0.05 |
| M&R Policy | Surface Compatibility | Unit Cost | |
|---|---|---|---|
| Do-nothing | PCC, APC | $0 | /sq. meter |
| Asphalt overlay | PCC, APC | $64.13 | /sq. meter |
| APC patching | APC | $339.48 | /sq. meter |
| APC crack sealing | APC | $14.76 | /meter * |
| PCC slab replacement | PCC | $433.95 | /sq. meter |
| PCC patching | PCC | $717.26 | /sq. meter |
| Model Description | Variable | Estimated Parameter | ||
|---|---|---|---|---|
| State 1 (APC) | Constant | 2.2606 | 26.03 | 0.000 |
| : Keel | −0.3759 | −3.17 | 0.002 | |
| : No. of APC patching | 1.2113 | 1.79 | 0.073 | |
| : No. of APC crack sealing | 0.4523 | 2.38 | 0.017 | |
| : keel | 1.7702 | 2.13 | 0.033 | |
| : outband | 1.4144 | 5.67 | 0.000 | |
| BIC = 582.7 | ||||
| State 1 (PCC) | Constant | 3.1883 | 14.33 | 0.000 |
| : No. of PCC patching | 8.7286 | 4.92 | 0.000 | |
| 1.6642 | 2.77 | 0.006 | ||
| BIC = 64.2 | ||||
| State 2 | Constant | 2.2516 | 15.56 | 0.000 |
| : PCC | 1.2833 | 2.98 | 0.003 | |
| 1.6551 | 2.99 | 0.003 | ||
| BIC = 177.9 |
| This Study | PAVER | |
|---|---|---|
| Methodology for pavement condition forecast | Stochastic duration models that yield transition probabilities of pavement condition over time | Simple extrapolation of historic records that yield deterministic pavement condition forecast |
| Methodology for pavement M&R planning | Network-level optimization that account for interdependence of M&R activities among pavements | M&R activities determined based on pavement condition thresholds and prioritization rules |
| System-level performance requirement | Constraining the maximum fractions of pavements allowed in states 2 and 3 | No constraints on the maximum fractions of pavements allowed in states 2 and 3 |
| Planning horizon | 2015–2030 | 2012–2021 |
| Total M&R cost | $63.9 million | $58.0 million |
| Average M&R cost per year | $4.0 million | $5.8 million |
| Major actions considered (% of total M&R cost) | Asphalt overlay (55.60) PCC slab replacement (0.02) | Asphalt overlay (93.65) PCC slab replacement (4.12) PCC reconstruction (1.77) |
| Minor actions considered (% of total M&R cost) | APC patching (32.51) APC crack sealing (1.60) PCC patching (10.27) | APC patching (0.21) APC crack sealing (0.22) PCC patching (0.03) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noruzoliaee, M.; Zou, B. Airfield Infrastructure Management Using Network-Level Optimization and Stochastic Duration Modeling. Infrastructures 2019, 4, 2. https://0-doi-org.brum.beds.ac.uk/10.3390/infrastructures4010002
Noruzoliaee M, Zou B. Airfield Infrastructure Management Using Network-Level Optimization and Stochastic Duration Modeling. Infrastructures. 2019; 4(1):2. https://0-doi-org.brum.beds.ac.uk/10.3390/infrastructures4010002
Chicago/Turabian StyleNoruzoliaee, Mohamadhossein, and Bo Zou. 2019. "Airfield Infrastructure Management Using Network-Level Optimization and Stochastic Duration Modeling" Infrastructures 4, no. 1: 2. https://0-doi-org.brum.beds.ac.uk/10.3390/infrastructures4010002