Equivalent Discharge Coefficient of Side Weirs in Circular Channel—A Lazy Machine Learning Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
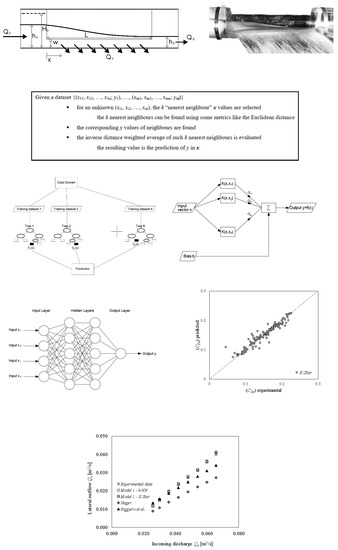
2.2. k Nearest Neighbor and K-Star
2.3. Random Forest
2.4. Support Vector Regression
2.5. Multilayer Perceptron
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Marchi, G. Saggio Di Teoria Del Funzionamento Degli Stramazzi Laterali. L Energ. Elettr. 1934, XI, 849–860. (In Italian) [Google Scholar]
- Gentilini, B. Ricerche Sperimentali Sugli Sfioratori Longitudinali. L Energ. Elettr. 1938, XV, 583–595. (In Italian) [Google Scholar]
- Ackers, P. A Theoretical Consideration of Side Weirs as Stormwater Overflows. Hydraulics Paper no 11. Symposium of Four Papers on Side Spillways. Proc. Inst. Civ. Eng. 1957, 6, 250–269. [Google Scholar] [CrossRef]
- Uyumaz, A.; Muslu, Y. Flow Over Side Weirs in Circular Channels. J. Hydraul. Eng. 1985, 111, 144–160. [Google Scholar] [CrossRef]
- Gisonni, C.; Hager, W.H. Short Sewer Sideweir. J. Irrig. Drain. Eng. 1997, 123, 354–363. [Google Scholar] [CrossRef]
- Oliveto, G.; Biggiero, V.; Fiorentino, M. Hydraulic Features of Supercritical Flow Along Prismatic Side Weirs. J. Hydraul. Res. 2001, 39, 73–82. [Google Scholar] [CrossRef]
- Castro Orgaz, O.; Hager, W.H. Subcritical Side-Weir Flow at High Lateral Discharge. J. Hydraul. Eng. 2012, 138, 777–787. [Google Scholar] [CrossRef]
- Michelazzo, G.; Oumeraci, H.; Paris, E. Laboratory Study on 3D Flow Structures Induced by Zero-Height Side Weir and Implications for 1D Modeling. J. Hydraul. Eng. 2015, 141, 04015023. [Google Scholar] [CrossRef]
- Hager, W.H. Supercritical Flow in Circular-Shaped Side Weir. J. Irrig. Drain. Eng. 1994, 120, 1–12. [Google Scholar] [CrossRef]
- Yen, B.C.; Wenzel, H.G. Dynamic Equations for Steady Spatially Varied Flow. J. Hydraul. Div. ASCE 1970, 96, 801–814. [Google Scholar]
- El Khashab, A.; Smith, K.V.H. Experimental Investigation of Flow Over Side Weirs. J. Hydraul. Div. ASCE 1976, 102, 1255–1268. [Google Scholar]
- Granata, F.; De Marinis, G.; Gargano, R.; Tricarico, C. Novel Approach for Side Weirs in Supercritical Flow. J. Irrig. Drain. Eng. 2013, 139, 672–679. [Google Scholar] [CrossRef]
- Biggiero, V.; Longobardi, D.; Pianese, D. Indagine Sperimentale Su Sfioratori Laterali a Soglia Bassa. G. Del. Genio Civ. 1994, 841, 183–199. (In Italian) [Google Scholar]
- Azimi, H.; Shabanlou, S.; Salimi, M.S. Free Surface and Velocity Field in a Circular Channel Along the Side Weir in Supercritical Flow Conditions. Flow Meas. Instrum. 2014, 38, 108–115. [Google Scholar] [CrossRef]
- Aydin, M.C. Investigation of a Sill Effect on Rectangular Side-Weir Flow by Using CFD. J. Irrig. Drain. Eng. 2015, 142, 04015043. [Google Scholar] [CrossRef]
- Hager, W.H. Lateral Outflow Over Side Weirs. J. Hydraul. Eng. 1987, 113, 491–504. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Swamee, P.K. Discharge Equations for Rectangular Sharp Crested Weirs. J. Hydraul. Eng. 1988, 114, 1082–1087. [Google Scholar] [CrossRef]
- Cheong, H. Discharge Coefficient of Lateral Diversion from Trapezoidal Channel. J. Irrig. Drain. Eng. 1991, 117, 461–475. [Google Scholar] [CrossRef]
- Singh, R.; Manivannan, D.; Satyanarayana, T. Discharge Coefficient of Rectangular Side Weirs. J. Irrig. Drain. Eng. 1994, 120, 814–819. [Google Scholar] [CrossRef]
- Swamee, P.K.; Pathak, S.K.; Ali, M.S. Side-Weir Analysis Using Elementary Discharge Coefficient. J. Irrig. Drain. Eng. 1994, 120, 742–755. [Google Scholar] [CrossRef]
- Borghei, S.M.; Jalili, M.R.; Ghodsian, M. Discharge Coefficient for Sharp-Crested Side Weir in Subcritical Flow. J. Hydraul. Eng. 1999, 125, 1051–1056. [Google Scholar] [CrossRef]
- Kaya, N.; Emiroglu, M.E.; Agaccioglu, H.; Agaçcioglu, H. Discharge Coefficient of a Semi-Elliptical Side Weir in Subcritical Flow. Flow Meas. Instrum. 2011, 22, 25–32. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; Santopietro, S. A Flow Field Characterization in a Circular Channel Along a Side Weir. Flow Meas. Instrum. 2016, 52, 92–100. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Xue, Y. M5 Model Trees and Neural Networks: Application to Flood Forecasting in the Upper Reach of the Huai River in China. J. Hydrol. Eng. 2004, 9, 491–501. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Etemad Shahidi, A.; Lim, S.Y. Scour Prediction in Long Contractions Using ANFIS and SVM. Ocean Eng. 2016, 111, 128–135. [Google Scholar] [CrossRef]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; De Marinis, G. Machine Learning Algorithms for the Forecasting of Wastewater Quality Indicators. Water 2017, 9, 105. [Google Scholar] [CrossRef]
- Granata, F.; De Marinis, G. Machine Learning Methods for Wastewater Hydraulics. Flow Meas. Instrum. 2017, 57, 1–9. [Google Scholar] [CrossRef]
- Granata, F.; Saroli, M.; De Marinis, G.; Gargano, R. Machine Learning Models for Spring Discharge Forecasting. Geofluids 2018, 2018, 8328167. [Google Scholar] [CrossRef]
- Diez Sierra, J.; Del Jesus, M. Subdaily Rainfall Estimation Through Daily Rainfall Downscaling Using Random Forests in Spain. Water 2019, 11, 125. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration Evaluation Models Based on Machine Learning Algorithms—A Comparative Study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Saadi, M.; Oudin, L.; Ribstein, P. Random Forest Ability in Regionalizing Hourly Hydrological Model Parameters. Water 2019, 11, 1540. [Google Scholar] [CrossRef]
- Emiroglu, M.E.; Kişi, O. Prediction of Discharge Coefficient for Trapezoidal Labyrinth Side Weir Using a Neuro-Fuzzy Approach. Water Resour. Manag. 2013, 27, 1473–1488. [Google Scholar] [CrossRef]
- Parsaie, A.; Haghiabi, A. The Effect of Predicting Discharge Coefficient by Neural Network on Increasing the Numerical Modeling Accuracy of Flow Over Side Weir. Water Resour. Manag. 2015, 29, 973–985. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Haghiabi, A.H.; Parsaie, A. Prediction of Side Weir Discharge Coefficient by Support Vector Machine Technique. Water Supply 2016, 16, 1002–1016. [Google Scholar] [CrossRef]
- Roushangar, K.; Khoshkanar, R.; Shiri, J. Predicting Trapezoidal and Rectangular Side Weirs Discharge Coefficient Using Machine Learning Methods. ISH J. Hydraul. Eng. 2016, 22, 1–8. [Google Scholar] [CrossRef]
- Azimi, H.; Bonakdari, H.; Ebtehaj, I. Sensitivity Analysis of the Factors Affecting the Discharge Capacity of Side Weirs in Trapezoidal Channels Using Extreme Learning Machines. Flow Meas. Instrum. 2017, 54, 216–223. [Google Scholar] [CrossRef]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-Based Learning Algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef] [Green Version]
- Cleary, J.G.; Trigg, L.E. K*: An Instance-Based Learner Using an Entropic Distance Measure. In Proceedings of the Machine Learning Proceedings, Tahoe, CA, USA, 9–12 July 1995; Elsevier: Amsterdam, The Netherlands, 1995; pp. 108–114. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer Science and Business Media LLC: Berlin, Germany, 1995. [Google Scholar]
- Baum, E.B. On the Capabilities of Multilayer Perceptrons. J. Complex. 1988, 4, 193–215. [Google Scholar] [CrossRef] [Green Version]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Input Determination for Neural Network Models in Water Resources Applications. Part 1. Background and Methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Fernando, T.; Maier, H.; Dandy, G.; Maier, H. Selection of Input Variables for Data Driven Models: An Average Shifted Histogram Partial Mutual Information Estimator Approach. J. Hydrol. 2009, 367, 165–176. [Google Scholar] [CrossRef]
- Galelli, S.; Humphrey, G.B.; Maier, H.R.; Castelletti, A.; Dandy, G.C.; Gibbs, M.S. An Evaluation Framework for Input Variable Selection Algorithms for Environmental Data-Driven models. Environ. Model. Softw. 2014, 62, 33–51. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Space Phys. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]















| Model | Number of Input Variables | Input Variables | No. of Hidden Layers | Number of Nodes |
|---|---|---|---|---|
| 1 | 5 | Qo*, Γ, Ho/w, L/D, Lw/D2 | 3 | 6, 10, 6 |
| 2 | 4 | Γ, Ho/w, L/D, Lw/D2 | 2 | 40, 2 |
| 3 | 3 | Γ, Ho/w, Lw/D2 | 3 | 3, 100, 3 |
| 4 | 3 | Γ, Ho/w, L/D | 3 | 3, 100, 2 |
| Nash–Sutcliffe Efficiency: It evaluates how the model fits experimental results and how well it predicts future outcomes. Hence, it represents a measure of the model accuracy. | |
| Mean Absolute Error: It is the average of the absolute values of the errors, therefore it is an indicator of the distance between the predictions and the observed values. | |
| Root Mean Square Error: It is the square root of the average of squared differences between predicted and experimental values. It has the advantage of penalizing large errors. | |
| Relative Absolute Error: It represents a normalized total absolute error. |
| Model | Input Variables | Algorithm | NSE | MAE | RMSE | RAE |
|---|---|---|---|---|---|---|
| 1 | Qo* | k-NN | 0.863 | 0.0103 | 0.0159 | 29.8% |
| Γ | K-Star | 0.912 | 0.0075 | 0.0119 | 21.7% | |
| Ho/w | RF | 0.865 | 0.0089 | 0.0147 | 26.0% | |
| L/D | SVR | 0.784 | 0.0128 | 0.0186 | 37.2% | |
| Lw/D2 | MLP | 0.602 | 0.0232 | 0.0314 | 67.5% | |
| 2 | k-NN | 0.857 | 0.0105 | 0.0161 | 30.6% | |
| Γ | K-Star | 0.845 | 0.0117 | 0.0166 | 34.1% | |
| Ho/w | RF | 0.843 | 0.0110 | 0.0159 | 32.1% | |
| L/D | SVR | 0.721 | 0.0150 | 0.0213 | 43.5% | |
| Lw/D2 | MLP | 0.587 | 0.0218 | 0.0304 | 63.4% | |
| 3 | k-NN | 0.477 | 0.0229 | 0.0329 | 66.5% | |
| Γ | K-Star | 0.185 | 0.0275 | 0.0387 | 79.9% | |
| Ho/w | RF | 0.441 | 0.0225 | 0.0305 | 65.4% | |
| Lw/D2 | SVR | 0.361 | 0.0270 | 0.0331 | 78.3% | |
| MLP | 0.302 | 0.0334 | 0.0404 | 96.9% | ||
| 4 | k-NN | 0.462 | 0.0213 | 0.0334 | 61.8% | |
| Γ | K-Star | 0.394 | 0.0202 | 0.0332 | 58.6% | |
| Ho/w | RF | 0.529 | 0.0192 | 0.029 | 55.7% | |
| L/D | SVR | 0.567 | 0.0179 | 0.0268 | 52.1% | |
| MLP | 0.612 | 0.0338 | 0.0416 | 98.3% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Granata, F.; Di Nunno, F.; Gargano, R.; de Marinis, G. Equivalent Discharge Coefficient of Side Weirs in Circular Channel—A Lazy Machine Learning Approach. Water 2019, 11, 2406. https://0-doi-org.brum.beds.ac.uk/10.3390/w11112406
Granata F, Di Nunno F, Gargano R, de Marinis G. Equivalent Discharge Coefficient of Side Weirs in Circular Channel—A Lazy Machine Learning Approach. Water. 2019; 11(11):2406. https://0-doi-org.brum.beds.ac.uk/10.3390/w11112406
Chicago/Turabian StyleGranata, Francesco, Fabio Di Nunno, Rudy Gargano, and Giovanni de Marinis. 2019. "Equivalent Discharge Coefficient of Side Weirs in Circular Channel—A Lazy Machine Learning Approach" Water 11, no. 11: 2406. https://0-doi-org.brum.beds.ac.uk/10.3390/w11112406