Direct Numerical Simulation of Sediment Transport in Turbulent Open Channel Flow Using the Lattice Boltzmann Method
Abstract
:1. Introduction
2. Numerical Methodology
2.1. Problem Description
2.2. Flow Solver
2.3. Treatments of Particle Interface
2.4. Treatments of Particle Movements
3. Simulation Settings and Validation
3.1. Simulation Settings
3.2. Code Validation
4. Results and Discussion
4.1. Fluid Statistics
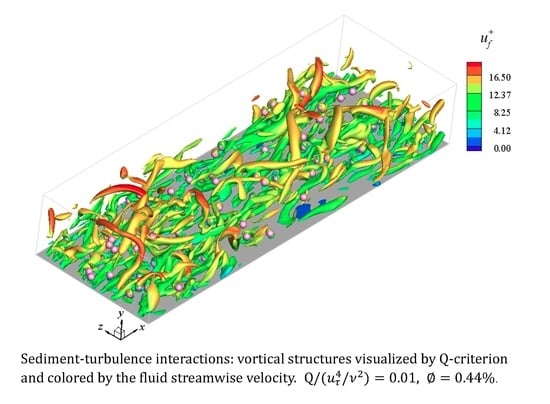
4.2. Flow Structures
4.3. Particle Statistics
4.4. Particle Dynamics
4.5. Particle Clustering
4.6. Discussion on the Particle Concentration Distribution
5. Conclusions
- (i)
- The presence of heavy particles substantially reduces the maximum fluid streamwise velocity fluctuations, and this effect is more pronounced at a higher particle volume fraction. In the near-wall region, the fluid wall-normal and spanwise velocity fluctuations are both augmented when compared to the single-phase flow. The particles force the TKE to distribute in a more isotropic manner and also make the TKE more homogeneous in the wall-normal direction.
- (ii)
- By visualizing the vortical structures, it is found that particles suppress the generation of the large-scale coherent vortices and simultaneously create numerous small-scale vortices in the near-wall region. Particles have a tendency to reside in the low-speed velocity regions and alter the streaky structures to a less organized state.
- (iii)
- Third itemThe particle TKE is much smaller than the fluid TKE except in the region very close to the wall. Under the current parameter settings, the normalized vertical particle concentration profiles are self-similar. Additionally, a general match between the present concentration profile and a theoretical model is found.
- (iv)
- Owing to the settling effect, most particles accumulate in the vicinity of the bottom wall, where the particle-wall and particle-particle collisions and the particle-turbulence interactions are strongest. By tracking the particle trajectories, different modes of the sediment transport, such as resuspension, saltation, and rolling, are captured.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rashidi, M.; Hetsroni, G.; Banerjee, S. Particle-turbulence interaction in a boundary layer. Int. J. Multiph. Flow 1990, 16, 935–949. [Google Scholar] [CrossRef]
- Baker, L.J.; Coletti, F. Experimental study of negatively buoyant finite-size particles in a turbulent boundary layer up to dense regimes. J. Fluid Mech. 2019, 866, 598–629. [Google Scholar] [CrossRef]
- Righetti, M.; Romano, G.P. Particle-fluid interactions in a plane near-wall turbulent flow. J. Fluid Mech. 2004, 505, 93–121. [Google Scholar] [CrossRef]
- Dwivedi, A.; Melville, B.W.; Shamseldin, A.Y.; Guha, T.K. Flow structures and hydrodynamic force during sediment entrainment. Water Resour. Res. 2011, 47, 499–509. [Google Scholar] [CrossRef]
- Balachandar, S.; Eaton, J.K. Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Maxey, M. Simulation methods for particulate flows and concentrated suspensions. Annu. Rev. Fluid Mech. 2017, 49, 171–193. [Google Scholar] [CrossRef]
- Tenneti, S.; Subramaniam, S. Particle-resolved direct numerical simulation for gas-solid flow model development. Annu. Rev. Fluid Mech. 2014, 46, 199–230. [Google Scholar] [CrossRef]
- Pan, Y.; Banerjee, S. Numerical investigation of the effects of large particles on wall-turbulence. Phys. Fluids 1997, 9, 3786–3807. [Google Scholar] [CrossRef]
- Kidanemariam, A.G.; Chan-Braun, C.; Doychev, T.; Uhlmann, M. DNS of horizontal open channel flow with finite-size, heavy particles at, low solid volume fraction. New J. Phys. 2013, 15, 025031. [Google Scholar] [CrossRef]
- Ji, C.N.; Munjiza, A.; Avital, E.; Ma, J.; Williams, J.J.R. Direct numerical simulation of sediment entrainment in turbulent channel flow. Phys. Fluids 2013, 25, 056601. [Google Scholar] [CrossRef]
- Yousefi, A.; Costa, P.; Brandt, L. Single sediment dynamics in turbulent flow over a porous bed-insights from interface-resolved simulations. J. Fluid Mech. 2020, 893. [Google Scholar] [CrossRef] [Green Version]
- Derksen, J.J. Simulations of granular bed erosion due to a mildly turbulent shear flow. J. Hydraul. Res. 2015, 53, 622–632. [Google Scholar] [CrossRef]
- Peng, C. Study of turbulence modulation by finite-size solid particles with the lattice Boltzmann method. Ph.D. Thesis, University of Delaware, Newark, DE, USA, 2018. [Google Scholar]
- Gao, H.; Li, H.; Wang, L.-P. Lattice Boltzmann simulation of turbulent flow laden with finite-size particle. Comput. Math. Appl. 2013, 65, 194–210. [Google Scholar] [CrossRef]
- Peng, C.; Wang, L.-P. Direct numerical simulations of turbulent pipe flow laden with finite-size neutrally buoyant particles at low flow Reynolds number. Acta Mech. 2019, 230, 517–539. [Google Scholar] [CrossRef]
- Peng, C.; Ayala, O.M.; Wang, L.-P. Flow modulation by a few fixed spherical particles in a turbulent channel flow. J. Fluid Mech. 2020, 884. [Google Scholar] [CrossRef]
- Tang, G.H.; Tao, W.Q.; He, Y.L. Lattice Boltzmann method for simulating gas flow in microchannels. Int. J. Mod. Phys. C 2004, 15, 335–347. [Google Scholar] [CrossRef] [Green Version]
- Rowiński, P.; Banaszkiewicz, M.; Pempkowiak, J.; Lewandowski, M.; Sarna, M. Hydrodynamics-Hydrodynamic and Sediment Transport Phenomena, 1st ed.; Springer: London, UK, 2014. [Google Scholar]
- Liu, X.; Ji, C.N.; Xu, X.L.; Xu, D.; Williams, J.J.R. Distribution characteristics of inertial sediment particles in the turbulent boundary layer of an open channel flow determined using Voronoï analysis. Int. J. Sediment Res. 2017, 32, 401–409. [Google Scholar] [CrossRef]
- Shao, X.M.; Wu, T.H.; Yu, Z.S. Fully resolved numerical simulation of particle-laden turbulent flow in a horizontal channel at a low Reynolds number. J. Fluid Mech. 2012, 693, 319–344. [Google Scholar] [CrossRef]
- Eshghinejadfard, A.; Zhao, L.H.; Thévenin, D. Lattice Boltzmann simulation of resolved oblate spheroids in wall turbulence. J. Fluid Mech. 2018, 849, 510–540. [Google Scholar] [CrossRef]
- Peng, Y.; Luo, L.S. A comparative study of immersed-boundary and interpolated bounce-back methods in LBE. Prog. Comput. Fluid Dyn. 2008, 8, 156–167. [Google Scholar] [CrossRef] [Green Version]
- Bouzidi, M.; Firdaouss, M.; Lallemand, P. Momentum transfer of a Boltzmann-lattice fluid with boundaries. Phys. Fluids 2001, 13, 3452–3459. [Google Scholar] [CrossRef]
- Zhao, W.F.; Yong, W.A. Single-node second-order boundary schemes for the lattice Boltzmann method. J. Comput. Phys. 2017, 329, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Wen, B.; Zhang, C.Y.; Tu, Y.S.; Wang, C.L.; Fang, H.P. Galilean invariant fluid-solid interfacial dynamics in lattice Boltzmann simulations. J. Comput. Phys. 2014, 266, 161–170. [Google Scholar] [CrossRef] [Green Version]
- Caiazzo, A.; Junk, M. Boundary forces in lattice Boltzmann: Analysis of momentum exchange algorithm. Comput. Math. Appl. 2008, 55, 1415–1423. [Google Scholar] [CrossRef]
- Brändle de Motta, J.C.; Breugem, W.P.; Gazanion, B.; Estivalezes, J.L.; Vincent, S.; Climent, E. Numerical modelling of finite-size particle collisions in a viscous fluid. Phys. Fluids 2013, 25, 083302. [Google Scholar] [CrossRef] [Green Version]
- Breugem, W.P. A combined soft-sphere collision/immersed boundary method for resolved simulations of particulate flows. In Proceedings of the ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting and 8th International Conference on Nanochannels, Microchannels, and Minichannels, Montreal, QC, Canada, 1–5 August 2010. [Google Scholar]
- Lammers, P.; Beronov, K.N.; Volkert, R.; Brenner, G.; Durst, F. Lattice BGK direct numerical simulation of fully developed turbulence in incompressible plane channel flow. Comput. Fluids 2006, 35, 1137–1153. [Google Scholar] [CrossRef]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T.M. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Blackwelder, R.F.; Eckelmann, H. Streamwise vortices associated with the bursting phenomenon. J. Fluid Mech. 1979, 94, 577–594. [Google Scholar] [CrossRef]
- Ebrahimian, M.; Sanders, R.S.; Ghaemi, S. Dynamics and wall collision of inertial particles in a solid-liquid turbulent channel flow. J. Fluid Mech. 2019, 881, 872–905. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef] [Green Version]
- Ni, J.R.; Wang, G.Q.; Borthwick, A.G.L. Kinetic theory for particles in dilute and dense solid-liquid flows. J. Hydraul. Eng. 2000, 126, 893–903. [Google Scholar] [CrossRef]
- Chan-Braun, C.; García-Villalba, M.; Uhlmann, M. Direct numerical simulation of sediment transport in turbulent open channel flow. In High Performance Computing in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lashgari, I.; Picano, F.; Costa, P.; Breugem, W.P.; Brandt, L. Turbulent channel flow of a dense binary mixture of rigid particles. J. Fluid Mech. 2017, 818, 623–645. [Google Scholar] [CrossRef] [Green Version]
- Robinson, S.K. Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 1991, 23, 601–639. [Google Scholar] [CrossRef]
- Wang, G.Q.; Ni, J.R. Kinetic theory for particle concentration distribution in two phase flow. J. Eng. Mech. 1990, 116, 2738–2748. [Google Scholar] [CrossRef] [Green Version]
- Rouse, H. Modern conceptions of the mechanics of turbulence. Trans. Am. Soc. Civ. Eng. 1937, 102, 463–505. [Google Scholar] [CrossRef]
- van Rijn, L.C. Sediment Transport, Part II: Suspended Load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]













Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Dong, Z.; Peng, C.; Wang, L.-P. Direct Numerical Simulation of Sediment Transport in Turbulent Open Channel Flow Using the Lattice Boltzmann Method. Fluids 2021, 6, 217. https://0-doi-org.brum.beds.ac.uk/10.3390/fluids6060217
Hu L, Dong Z, Peng C, Wang L-P. Direct Numerical Simulation of Sediment Transport in Turbulent Open Channel Flow Using the Lattice Boltzmann Method. Fluids. 2021; 6(6):217. https://0-doi-org.brum.beds.ac.uk/10.3390/fluids6060217
Chicago/Turabian StyleHu, Liangquan, Zhiqiang Dong, Cheng Peng, and Lian-Ping Wang. 2021. "Direct Numerical Simulation of Sediment Transport in Turbulent Open Channel Flow Using the Lattice Boltzmann Method" Fluids 6, no. 6: 217. https://0-doi-org.brum.beds.ac.uk/10.3390/fluids6060217