Computational Fluid Dynamics Approach for Oscillating and Interacting Convective Flows
Abstract
:1. Introduction
2. The Numerical Approach
2.1. The Simulation Code
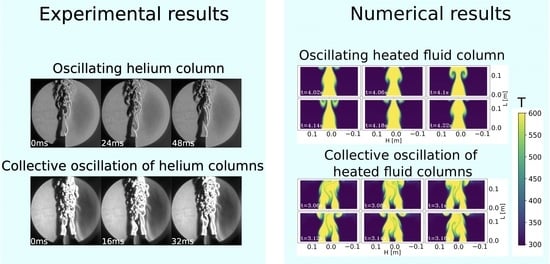
2.2. Simulating the Rising Hot Air Column
2.3. Numerical Results for the Oscillation Frequency
2.4. Numerical Results for the Collective Behavior
3. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Solving the 2D Poisson Equation in FEniCS
| from fenics import ∗ # |
| import numpy as np #Numpy is required for error calculation |
| import matplotlib.pyplot as plt #We plot the result with the matplotlib |
| Nx=10#The number of grid points in the x directions |
| Ny=10#The number of grid points in the y directions |
| mesh=UnitSquareMesh(Nx,Ny) |
| V=FunctionSpace(mesh,’P’,1)#space containing first degree polynomials |
| fi_D=Expression(’1+x[0]∗x[0]+2∗x[1]∗x[1]’,degree=2) |
| #boundary conditions equation (on boundarys fi(x,y)=x^2+2y^2+1) |
| def boundery(x, on_boundary): |
| return on_boundary |
| bc=DirichletBC(V,fi_D,boundery)#boundary conditions |
| fi=TrialFunction(V) |
| v=TestFunction(V) |
| f=Constant(-6) |
| a=dot(grad(fi),grad(v))∗dx#right side of equation |
| L=f∗v∗dx#left side of equation |
| fi=Function(V) |
| solve(a==L,u,bc)#solve the~equation |
| c = plot(interpolate(fi, V), mode=’color’) |
| plt.colorbar(c) |
| plot(fi) |
| plt.savefig(’result1.png’) |
| plt.show() |
| vertex_v_ud=fi_D.compute_vertex_values(mesh) |
| err_max=np.max(np.abs(vertex_v_ud-vertex_v_u) |
| print("maximum ̺ error: ̺ ",err_max) |
Appendix A.2. Test for the 2D Fluid Dynamics Simulations—Karman Vortices

Appendix A.3. Test for the 2D Fluid Dynamics Simulations—Heat Induced Mushroom Cloud

References
- Gergely, A.; Paizs, C.; Tötös, R.; Néda, Z. Oscillations and collective behavior in convective flows. Phys. Fluids 2021, 33, 124104. [Google Scholar] [CrossRef]
- Monkewitz, P.; Sohn, K. Absolute instability in hot jets. AIAA J. 1988, 26, 911–916. [Google Scholar] [CrossRef]
- Sreenivasan, K.; Raghu, S.; Kyle, D. Absolute instability in variable density round jets. Exp. Fluids 1989, 7, 309. [Google Scholar] [CrossRef]
- Yuan, T.; Durox, D.; Villermaux, E. An analogue study for flame flickering. Exp. Fluids 1994, 17, 337–349. [Google Scholar] [CrossRef]
- Monkewitz, P.; Bechert, D.; Barsikow, B.; Lehmann, B. Self-excited oscillations and mixing in a heated round jet. J. Fluid Mech. 1990, 213, 611–639. [Google Scholar] [CrossRef]
- Lesshafft, L.; Huerre, P.; Sagaut, P. Frequency selection in globally unstable round jets. Phys. Fluids 2007, 19, 054108. [Google Scholar] [CrossRef] [Green Version]
- Boguslawski, A.; Tyliszczak, A.; Drobniak, S.; Asendrych, D. Self-sustained oscillations in a homogeneous-density round jet. J. Turbul. 2013, 14, 25–52. [Google Scholar] [CrossRef]
- Pawlowska, A.; Boguslawski, A. The Dynamics of Globally Unstable Air-Helium Jets and Its Impact on Jet Mixing Intensity. Processes 2020, 8, 1667. [Google Scholar] [CrossRef]
- Jendoubi, S.; Strykowski, P. Absolute and convective instability of axisymmetric jets with external flow. Phys. Fluids 1994, 6, 3000. [Google Scholar] [CrossRef]
- Chamberlin, D.; Rose, A. The flicker of luminous flames. Proc. Symp. Combust. 1948, 1–2, 27–32. [Google Scholar] [CrossRef]
- Durox, D.; Yuan, T.; Baillot, F.; Most, J. Premixed and diffusion flames in a centrifuge. Combust. Flame 1995, 102, 501–511. [Google Scholar] [CrossRef]
- Durox, D.; Yuan, T.; Villermaux, E. The Effect of Buoyancy on Flickering in Diffusion Flames. Combust. Sci. Technol. 1997, 124, 277–294. [Google Scholar] [CrossRef]
- Huang, Y.; Yan, Y.; Lu, G.; Reed, A. On-line flicker measurement of gaseous flames by image processing and spectral analysis. Meas. Sci. Technol. 1999, 10, 726–733. [Google Scholar] [CrossRef]
- Kitahata, H.; Taguchi, J.; Nagayama, M.; Sakurai, T.; Ikura, Y.; Osa, A.; Sumino, Y.; Tanaka, M.; Yokoyama, E.; Miike, H. Oscillation and Synchronization in the Combustion of Candles. J. Phys. Chem. A 2009, 113, 8164–8168. [Google Scholar] [CrossRef]
- Ghosh, S.; Mondal, S.; Mondal, T.; Mukhopadhyay, A.; Sen, S. Dynamic Characterization of Candle Flame. Int. J. Spray Combust. Dyn. 2010, 2, 267–284. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, K.; Kijima, A.; Umeno, Y.; Shima, H. Synchronization in flickering of three-coupled candle flames. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guo, X.; Jia, J.; Xiao, J. Frequency and Phase Characteristics of Candle Flame Oscillation. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Gergely, A.; Sándor, B.; Paizs, C.; Tötös, R.; Néda, Z. Flickering candle flames and their collective behavior. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Settles, G.S. Schlieren and Shadowgraph Techniques: Visualizing Phenomena in Transparent Media; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Leptuch, P.A.; Agrawal, A.K. High-speed rainbow schlieren visualization of an oscillating helium jet undergoing gravitational change. J. Vis. 2006, 9, 101–109. [Google Scholar] [CrossRef] [Green Version]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man, Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- FreddyCree. Wikipedia, Otsu’s Method. 2017. Available online: https://en.wikipedia.org/wiki/Otsu’s_method (accessed on 10 July 2021).
- Gergely, A. 2020. Available online: https://youtube.com/playlist?list=PLamJmxTyiR_3sy-fYUEDEXW4NtbsnsXnW (accessed on 15 July 2022).
- Joel, H.; Ferziger, M.P.; Street, R.L. Computational Methods for Fluid Dynamics, 4th ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Wendt, J.F. Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Venkatakrishnan, V.; Salas, M.D.; Chakravarthy, S.R. Barriers and Challenges in Computational Fluid Dynamics; Springer Science+Business Media Dordrecht: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Correa, P.G.; MacIntyre, J.; Gomba, J.; Cachile, M.; Hulin, J.; Auradou, A. Three-dimensional flow structures in X-shaped junctions: Effect of the Reynolds number and crossing angle. Phys. Fluids 2019, 31, 043606. [Google Scholar] [CrossRef]
- Gergely, A. Heated Air Column. 2020. Available online: https://youtube.com/playlist?list=PLamJmxTyiR_0fNk5bzTD5GyRF_dOrmB2E (accessed on 10 July 2022).
- Langtangen, H.P.; Logg, A. Solving PDEs in Python; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Logg, A.; Mardal, K.A.; Wells, G.N. Automated Solution of Differential Equations by the Finite Element Method; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]















| d [m] | 0.04 | 0.06 | 0.08 | 0.1 | 0.12 | 0.14 |
|---|---|---|---|---|---|---|
| ms | 6781 | 1952 | 800 | 398 | 223 | 136 |
| d [m] | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|
| ms | 0.45 | 0.3 | 0.21 | 0.153 | 0.11 | 0.088 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gergely, A.; Néda, Z. Computational Fluid Dynamics Approach for Oscillating and Interacting Convective Flows. Fluids 2022, 7, 339. https://0-doi-org.brum.beds.ac.uk/10.3390/fluids7110339
Gergely A, Néda Z. Computational Fluid Dynamics Approach for Oscillating and Interacting Convective Flows. Fluids. 2022; 7(11):339. https://0-doi-org.brum.beds.ac.uk/10.3390/fluids7110339
Chicago/Turabian StyleGergely, Attila, and Zoltán Néda. 2022. "Computational Fluid Dynamics Approach for Oscillating and Interacting Convective Flows" Fluids 7, no. 11: 339. https://0-doi-org.brum.beds.ac.uk/10.3390/fluids7110339