Schedule Execution for Two-Machine Job-Shop to Minimize Makespan with Uncertain Processing Times

Abstract

This study addresses a two-machine job-shop scheduling problem with fixed lower and upper bounds on the job processing times. An exact value of the job duration remains unknown until completing the job. The objective is to minimize a schedule length (makespan). It is investigated how to best execute a schedule, if the job processing time may be equal to any real number from the given (closed) interval. Scheduling decisions consist of the off-line phase and the on-line phase of scheduling. Using the fixed lower and upper bounds on the job processing times available at the off-line phase, a scheduler may determine a minimal dominant set of schedules (minimal DS), which is based on the proven sufficient conditions for a schedule dominance. The DS optimally covers all possible realizations of the uncertain (interval) processing times, i.e., for each feasible scenario, there exists at least one optimal schedule in the minimal DS. The DS enables a scheduler to make the on-line scheduling decision, if a local information on completing some jobs becomes known. The stability approach enables a scheduler to choose optimal schedules for most feasible scenarios. The on-line scheduling algorithms have been developed with the asymptotic complexity $O(n^2)$ for n given jobs. The computational experiment shows the effectiveness of these algorithms.

1. Introduction

Many real-world production planning and scheduling problems have various uncertainties. Different approaches are used for solving the uncertain planning and scheduling problems. In particular, a stability approach [1,2,3,4] for solving sequencing and scheduling problems with the interval uncertainty is based on the stability analysis of the optimal job permutations (schedules) to possible variations of the job processing times (durations). In this paper, this approach is applied to the uncertain two-machine job-shop scheduling problem, where a job processing time is only known once the job is completed. Although, the exact value of the job processing time is unknown before scheduling, it is known that the processing time must have a value no less than the lower bound and no greater than the upper bound available before scheduling. It should be noted that uncertainties of the job processing times are due to some external forces in contrast to scheduling problems with controllable processing times [5,6,7], where the objective is to determine optimal processing times and then to find an optimal schedule for the jobs with the chosen processing times.

1.1. Research Motivation

It is not realistic to assume processing times are exactly known and fixed for many scheduling problems arising in real-world situations. For such an uncertain scheduling problem, job processing times are random variables. Moreover, it is often hard to obtain probability distributions for all random processing times of the jobs to be processed. In such cases, schedules constructed due to assuming certain probability distributions are often not close to the optimal schedule. Although, the probability distribution of the job processing time may not be known before scheduling, the upper and lower bounds on the job processing time are easy to obtain in most practical scheduling environments. The available information on these lower and upper bounds on the job processing times should be utilized in finding optimal schedules for the scheduling problem with an interval uncertainty.

Since there may not exist a unique schedule that remains optimal for all possible realizations of the job processing times (all possible scenarios), it is desirable to construct a minimal dominant set of schedules (permutations of the jobs to be processed), which dominate all other ones. At the off-line phase of scheduling (i.e., before starting an execution of the constructed schedule), a minimal dominant set of schedules may be determined based on the proven dominance relations [8].

If the constructed minimal dominant set of schedules is a singleton, then a single schedule remaining optimal for all possible scenarios exists. Otherwise, one can reduce the size of the determined minimal dominant set of schedules at the on-line phase of scheduling based on the additional information about completing some jobs. This additional on-line information allows a scheduler to find new dominance relations in order to best execute a schedule. It is clear that on-line scheduling decisions must be realized very quickly. In other words, only polynomial algorithms may be applied at the on-line phase of scheduling.

1.2. Contributions of This Research

In this paper, it is shown how to determine a minimal dominant set of schedules that would contain at least one optimal schedule for every scenario that is possible. The necessary and sufficient conditions are proven for the existence of a single pair of job permutations, which is optimal for the two-machine job-shop scheduling problem with any possible scenario. The algorithms have been developed for testing a set of the proven sufficient conditions for a schedule dominance and for the realization of a schedule, which is either optimal or very close to optimal one for the factual scenario. The developed algorithms are polynomial in the number n of the given jobs. Their asymptotic complexities do not exceed $O(n^2)$. The computational experiments on a large number of randomly generated instances of the uncertain (interval) two-machine job-shop scheduling problem show the efficiency and effectiveness of the developed off-line and on-line algorithms and programs. For different distributions of the factual job processing times, the developed on-line algorithms perform with the maximal errors of the achieved makespan less than $1\%$ provided that $n \in \{20,30,\dots ,100\}$. For all tested classes of the randomly generated instances, the average makespan errors ${\Delta }_{ave}\%$ for all tested numbers $n \in \{10,20,\cdots ,100\}$ of jobs $\mathcal{J}$ are less than $0.02\%$. Each tested series of 1000 randomly generated instances was solved within no more than one second.

The paper is organized as follows. Settings of the considered scheduling problems with the interval uncertainty and main notation are introduced in Section 2. A literature review is presented in Section 3. The results published for the uncertain (interval) scheduling flow-shop problem are discussed in Section 3.2. These results are used in Section 4 for finding the optimal job permutations at the off-line phase of scheduling. In Section 4.2, the precedence digraphs are described for determining a minimal dominant set of schedules. An illustrative example is considered in Section 4.3. The on-line phase of scheduling is investigated in Section 5, where two theorems for the dominant sets of schedules have been proven. Section 6 contains the algorithms developed for the on-line phase of scheduling, illustrative examples (Section 6.2) and the discussion of the conducted computational experiments (Section 6.3). Appendix B consists of the tables with the detailed computational results. Some concluding remarks are made in Section 7.

2. Settings of Scheduling Problems and Main Notations

A set $\mathcal{J}=\{J_1,J_2,\dots ,J_n\}$ of the given jobs must be processed on different machines from a set $\mathcal{M}=\{M_1,M_2\}$. All jobs are available for processing from the same time $t=0$. Using the standard notation $\alpha \left|\beta \right|\gamma$ [9], this deterministic two-machine job-shop scheduling problem to minimize the makespan is denoted as follows: $J2|n_i\le 2|C_{max}$, where $\alpha =J2$ means a job-shop processing system with two available different machines and $n_i$ a number of possible stages for processing a job $J_i \in \mathcal{J}$. The criterion $\gamma =C_{max}$ determines the minimization of a schedule length (makespan) as follows:

$$C_{max}:=\underset{s\in S}{min}{C}_{max}\left(s\right)=\underset{s\in S}{min}\{max\{C_i\left(s\right):J_i\in \mathcal{J}\}\},$$

(1)

where $C_i\left(s\right)$ denotes the completion time-point of the job $J_i \in \mathcal{J}$ in the schedule s and S denotes a set of all semi-active schedules existing for the deterministic problem $J2|n_i\le 2|C_{max}$. (A schedule s is called a semi-active one [10,11,12] if the completion time-point $C_i\left(s\right)$ of any job $J_i \in \mathcal{J}$ cannot be reduced without changing an order of the jobs on some machine.)

Let $O_{ij}$ denote an operation of the job $J_i \in \mathcal{J}$ processed on the machine $M_j \in \mathcal{M}$. Each of the available machines can process the job $J_i \in \mathcal{J}$ no more than once, a preemption of the operation $O_{ij}$ being not allowed. The job $J_i \in \mathcal{J}$ has its own processing route through the available machines in set $\mathcal{M}$. The partition $\mathcal{J}={\mathcal{J}}_1\bigcup {\mathcal{J}}_2\bigcup {\mathcal{J}}_{1,2}\bigcup {\mathcal{J}}_{2,1}$ of the jobs is given and fixed, where each job $J_i \in {\mathcal{J}}_{1,2}$ must be processed first on machine $M_1$ and then on machine $M_2$, i.e., all jobs from the set ${\mathcal{J}}_{1,2}$ have the same machine route ($M_1,M_2$). Each job $J_i\in {\mathcal{J}}_{2,1}$ has an opposite machine route ($M_2,M_1$). The set ${\mathcal{J}}_j$, where $j \in \{1,2\}$, consists of all jobs, which must be processed only on one machine $M_j \in \mathcal{M}$. The following notation $m_h=\left|{\mathcal{J}}_h\right|$ will be used, where $h \in \{1;2;1,2;2,1\}$.

In this research, it is investigated the uncertain (interval) two-machine job-shop scheduling problem denoted as $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$, where the duration $p_{ij}$ of each operation $O_{ij}$ is unknown before scheduling. It is only known that the inclusion $p_{ij} \in [l_{ij},u_{ij}]$ holds for any possible realization of the chosen schedule, where $u_{ij}\ge l_{ij}\ge 0$. It is also assumed that a probability distribution of the random duration of a job from the set $\mathcal{J}$ is also unknown before scheduling. Let a set T of all possible scenarios $p=(p_{1,1},p_{1,2},\dots ,$$p_{n1},p_{n2})$ of the job processing times be determined as follows:

$$T=\{p:l_{ij}\le p_{ij}\le u_{ij},J_i \in \mathcal{J},M_j\in \mathcal{M}\}.$$

It should be noted that the problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ is mathematically incorrect since one cannot calculate makespan $C_{max}\left(s\right)$ in the equality (1) before completing the jobs $J_i$ in the set $\mathcal{J}$ provided that the strict inequality $u_{ij}>l_{ij}$ holds. Moreover, in most cases there does not exist a schedule, which is optimal for all possible scenarios $p \in T$ for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. Therefore, one cannot solve most such uncertain (interval) scheduling problems in the generally accepted sense.

In [13], it is proven that the deterministic job-shop problem $J2|n_i\le 2|C_{max}$ is solvable in $O(nlogn)$ time. The optimal semi-active schedule for this deterministic problem is determined as the pair $({\pi }^{\prime },{\pi }^{″})$ of two job permutations (called a Jackson’s pair of permutations), where ${\pi }^{\prime }=({\pi }_{1,2},{\pi }_1,{\pi }_{2,1})$ is an optimal permutation of the jobs ${\mathcal{J}}_1\bigcup {\mathcal{J}}_{1,2}\bigcup {\mathcal{J}}_{2,1}$ processed on machine $M_1$ and ${\pi }^{″}=({\pi }_{2,1},{\pi }_2,{\pi }_{1,2})$ is an optimal permutation of the jobs ${\mathcal{J}}_2\bigcup {\mathcal{J}}_{1,2}\bigcup {\mathcal{J}}_{2,1}$ on machine $M_2$. Such an optimal semi-active schedule is presented in Figure 1. In what follows, it is assumed that job $J_i$ belongs to the permutation ${\pi }_h$, if the following inclusion holds: $J_i \in {\mathcal{J}}_h$.

In a Jackson’s pair of permutations $({\pi }^{\prime },{\pi }^{″})$, the optimal order for processing jobs from the set ${\mathcal{J}}_1$ (from the set ${\mathcal{J}}_2$, respectively) may be arbitrary (due to this, we fix them in the increasing order of their indexes). For the permutation ${\pi }_{1,2}$ (permutation ${\pi }_{2,1}$, respectively), the following inequality holds:

$$min\{p_{i_{e}1},p_{i_{f}2}\}\le min\{p_{i_{f}1},p_{i_{e}2}\}$$

(2)

for all indexes e and f provided that $1\le e<f\le m_{1,2}$ ($1\le f<e\le m_{2,1}$, respectively). The permutation ${\pi }_{1,2}$ (permutation ${\pi }_{2,1}$) is called a Johnson’s permutation; see [14].

The deterministic scheduling problem $J2|n_i\le 2|C_{max}$ associated with a fixed scenario p of the job processing times is an individual deterministic problem. In what follows, this problem is denoted as follows: $J2|p,n_i\le 2|C_{max}$. For any fixed scenario $p \in T$, there exists a Jackson’s pair $({\pi }^{\prime },{\pi }^{″})$ of permutations, which is optimal for the problem $J2|p,n_i\le 2|C_{max}$, i.e., the equality $C_{max}({\pi }^{\prime },{\pi }^{″})=C_{max}^p$ holds, where $C_{max}^p$ denotes the optimal makespan value for the problem $J2|p,n_i\le 2|C_{max}$.

Let $S_{1,2}$ denote a set of all permutations of $m_{1,2}$ jobs from the set ${\mathcal{J}}_{1,2}$, where $|S_{1,2}|=m_{1,2}!$. The set $S_{2,1}$ is a set of all permutations of $m_{2,1}$ jobs from the set ${\mathcal{J}}_{2,1}$, $|S_{2,1}|=m_{2,1}!.$

Let the set $S=<S_{1,2},S_{2,1}>$ be a subset of the Cartesian product $(S_{1,2},{\pi }_1,S_{2,1})\times (S_{2,1},{\pi }_2,S_{1,2})$, each element of the set S being a pair of job permutations $({\pi }^{\prime },{\pi }^{″}) \in S$, where ${\pi }^{\prime }=({\pi }_{1,2}^i,{\pi }_1,{\pi }_{2,1}^j)$ and ${\pi }^{″}=({\pi }_{2,1}^j,{\pi }_2,{\pi }_{1,2}^i)$ with inequalities $1\le i\le m_{1,2}!$ and $1\le j\le m_{2,1}!$. It is known that the set S determines all semi-active schedules and vice versa; see [12]. Since index i (and index j) is the same in each permutation from the pair $({\pi }^{\prime },{\pi }^{″}) \in S$ and it is a fixed permutation ${\pi }_1$ (permutation ${\pi }_2$), the equality $\left|S\right|=m_{1,2}!·m_{2,1}!$ holds. The following definition of a J-solution is used for the uncertain (interval) job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$.

Definition 1.

An inclusion-minimal set of the pairs of job permutations $S\left(T\right)\subseteq S$ is called a J-solution for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the set $\mathcal{J}$ of the given jobs, if for each scenario $p \in T$, the set $S\left(T\right)$ contains at least one pair $({\pi }^{\prime },{\pi }^{″}) \in S$ of job permutations that is optimal for the individual deterministic problem $J2|p,n_i\le 2|C_{max}$ with a fixed scenario p.

From Definition 1, it follows that for any proper subset $S^{\prime }$ of the set $S\left(T\right)$, $S^{\prime }\subset S\left(T\right)$, there exists a scenario $p^{\prime } \in T$ such that the set $S^{\prime }$ does not contain an optimal pair of job permutations for the individual deterministic problem $J2|p^{\prime },n_i\le 2|C_{max}$ with a fixed scenario $p^{\prime }$.

3. A Literature Review and Closed Results

It should be noted that the uncertain flow-shop scheduling problem denoted as $F2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ is well studied [15], unlike the uncertain job-shop scheduling problem.

3.1. Approaches to Scheduling Problems with Different Forms of Uncertainties

For the well-known stochastic approach, it is assumed that the job processing times are random variables with certain probability distributions determined before scheduling. There are two types of the stochastic scheduling problems [10], where one is on stochastic jobs and another is on stochastic machines. In the stochastic job scheduling problem, each job processing time is a random variable with a known probability distribution. With the objective of minimizing the expected makespan value, the flow-shop problem was studied in [16,17,18]. In the stochastic machine scheduling problem, each job processing time is a constant, while each completion time of the given job is a random variable due to the machine breakdown or machine non-availability. In [19,20,21], the flow-shop scheduling problems to stochastically minimize either makespan or total completion time were investigated.

If it is impossible to determine probability distributions for all random job processing times, other approaches have to be used [11,22,23,24,25]. In the approach of seeking a robust schedule [22,26,27,28], a decision-maker looks for a schedule that hedges against the worst-case possible scenario.

A fuzzy approach [29,30,31,32,33,34,35] allows a scheduler to find best schedules with respect to fuzzy processing times of the jobs to be processed. The work of [35] addresses to the job-shop scheduling problem with uncertain processing times modeled as triangle fuzzy numbers, where the criterion is to minimize the expected makespan value. Based on the disjunctive graph model of the job-shop problem, a definition of criticality is proposed for this job-shop problem along with neighborhood structure for a local search. It is shown that the proposed neighborhood structure has two properties: feasibility and connectivity, which allow a scheduler to improve the efficiency of the local search and to ensure asymptotic convergence (in probability) to a globally optimal solution of the uncertain job-shop problem. The conducted computational experiments supported these theoretical results.

The stability approach was developed in [1,4,36,37] for the $C_{max}$ criterion, and in [2,38,39,40] for the total completion time criterion, $\sum C_i:={\sum }_{J_i\in \mathcal{J}}{C}_i\left({\pi }^{\prime }\right)$. The aim of this approach is to construct a minimal dominant set $S\left(T\right)$ of schedules, which optimally covers all feasible scenarios T. The dominant set $S\left(T\right)$ is used in the multi-phase decision framework; see [41]. The set $S\left(T\right)$ is constructed at the first off-line phase of scheduling. Based on the set $S\left(T\right)$, it is possible to find a schedule remaining optimal for most feasible scenarios. The set $S\left(T\right)$ enables a scheduler to execute best a schedule in most cases of the uncertain flow-shop scheduling problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ [41].

The stability radius of the optimal semi-active schedule was studied in [4], where a formula for calculating the stability radius and corresponding algorithms were described and tested.

In [36], the sufficient conditions were proven when a transposition of the given jobs minimizes the makespan criterion. The work of [42] addressed the objective criterion $\sum C_i$ in the uncertain two-machine flow-shop scheduling problem. The case of separate setup times with the criterion of minimizing a total completion time or makespan was investigated in [43].

For the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$, an additional criterion is often introduced. In particular, a robust schedule minimizing the worst-case deviation from the optimal value was proposed in [44] to hedge against the interval or discrete uncertainties. In [45], a binary NP-hardness was proven for finding a pair $({\pi }_q,{\pi }_q) \in S$ of the identical job permutations that minimizes the worst-case absolute regret for the uncertain two-machine flow-shop problem with the criterion $C_{max}$ and only two possible scenarios. In [46], a branch and bound method was developed for the uncertain job-shop scheduling problem to minimize makespan and optimize robustness based on a mixed graph model and the propositions proposed in [47]. The effectiveness of the developed algorithm was clarified by solving test uncertain job-shop scheduling problems.

The work of [48] addresses robust scheduling for a flexible job-shop scheduling problem with a random machine breakdown. Two objectives makespan and robustness were considered. Robustness was indicated by the expected value of the relative difference between the deterministic and factual makespan values. Two measures for robustness have been developed. The first suggested measure considers the probability of machine breakdowns. The second measure considers the location of float times and machine breakdowns. A multi-objective evolutionary algorithm is presented and experimentally compared with several other existing measures.

A function of predictive scheduling in order to obtain a stable and robust schedule for a shop floor was investigated in [49]. An innovative maintenance planning and production scheduling method has been proposed. The proposed method uses a database to collect information about failure-free times, a prediction module of failure-free times, predictive rescheduling module, a module for evaluating the accuracy of prediction and maintenance performance. The proposed approach is based on probability theory and applied for solving a job-shop scheduling problem. For unpredicted failures, a rescheduling procedure was also developed. The evaluation procedure provides information about the degradation of a performance measure and the stability of a schedule.

The simulation and experimental design methods play a useful role in solving job-shop scheduling problems with uncertain parameters (see survey [50], where many studies about dynamic and static job-shop scheduling problems with material handling are described and systematized).

In [51], a quality robustness and a solution robustness were investigated in order to compare the operational efficiency of the job-shop in the events of machine failures. Two well-known proactive approaches were compared to compute the operational efficiency of the job-shop with unpredicted machine failures. In the computational experiments, the predictive-reactive approach (without a prediction) and the proactive-reactive one (with a prediction) were applied for the job-shop model with possible disruptions. The computational results of computer simulations for the above two approaches were compared in order to select better schedules for reducing costs and waste due to machine failures.

The paper [52] presents a methodological pattern to assess the effectiveness of Order Review and Release (ORR) techniques in a job-shop environment. It is presented a comparison among three ORR approaches, i.e., a time bucketing approach, a probabilistic approach and a temporal approach. Simulation results highlighted that the performances of the ORR techniques tested depend on how perturbed the environment, where they are implemented, is. Based on a computer simulation, it was shown that the ORR techniques greatly differ in their robustness against environment perturbations.

The paper [53] presents an effective heuristic algorithm for the job-shop problem with uncertain arrival times of the jobs, processing times, due dates and part priorities. A separable problem formulation that balances modeling accuracy and solution complexity is described with the goal to minimize expected part tardiness and earliness cost. The optimization is subject to arrival times and operation precedence constraints (for each possible realization), and machine capacity constraints (in the expected value sense). The solution algorithm based on a Lagrangian relaxation and stochastic dynamic programming was developed to obtain dual solutions. The computational complexity of the developed algorithm is only slightly higher than the one without considering uncertainties of the numerical parameters. Numerical testing supported by a simulation demonstrated that near optimal solutions were obtained, and uncertainties are effectively handled for problems of practical sizes.

The published results on the application of the stability approach for the uncertain two-machine flow-shop problem are presented in Section 3.2. These results are described in detail since they are used for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ in Section 4, Section 5 and Section 6.

3.2. Closed Results for Uncertain (Interval) Flow-Shop Scheduling Problems

The uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ is a generalization of the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$, where all given jobs have the same machine route. Two uncertain flow-shop problems are associated with an uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. In one of these flow-shop problems, an optimal schedule for processing the jobs ${\mathcal{J}}_{1,2}$ must be determined, i.e., it is assumed that ${\mathcal{J}}_{2,1}={\mathcal{J}}_1={\mathcal{J}}_2=\varnothing$. In another associated flow-shop problem, an optimal schedule for processing jobs ${\mathcal{J}}_{2,1}$ must be determined, i.e., it is assumed that ${\mathcal{J}}_{1,2}={\mathcal{J}}_1={\mathcal{J}}_2=\varnothing$. Our approach to the solution of the uncertain job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ is based on the following remark.

Remark 1.

The solution of the uncertain job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ may be based on the solutions of the associated flow-shop scheduling problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_{1,2}$, where ${\mathcal{J}}_{2,1}={\mathcal{J}}_1={\mathcal{J}}_2=\varnothing$, and that with the job set $\mathcal{J}={\mathcal{J}}_{2,1}$ (i.e., ${\mathcal{J}}_{1,2}={\mathcal{J}}_1={\mathcal{J}}_2=\varnothing$).

The sense of Remark 1 becomes clear from Figure 2, where the semi-active schedule s for the job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ is presented. Indeed, in Figure 2, the length $C_{max}\left(s\right)$ of the schedule s is equal to the length of the corresponding semi-active schedule determined for the associated flow-shop scheduling problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_{1,2}$. Thus, if one will solve both associated flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_{1,2}$ and associated flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_{2,1}$, then the original job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ will be also solved.

We next observe in detail the results obtained for the two-machine flowshop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_{1,2}$. For using the above notations introduced for the uncertain job-shop problem, we need the following remark for the uncertain flow-shop problem.

Remark 2.

The considered problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ has the following two mandatory properties:

(i)

the set S is a set of $n!$ pairs $({\pi }_q,{\pi }_q)$ of the identical permutations of $n=m_{1,2}$ jobs from the set $\mathcal{J}={\mathcal{J}}_{1,2}$ since the machine route for processing all jobs ${\mathcal{J}}_{1,2}$ is the same $(M_1,M_2)$;

(ii)

the J-solution (see Definition 1) is a set of Johnson’s permutations of the jobs $\mathcal{J}={\mathcal{J}}_{1,2}$, i.e., for each scenario $p \in T$ the set $S\left(T\right)$ contains at least one optimal pair $({\pi }_q,{\pi }_q)$ of identical Johnson’s permutations ${\pi }_q$ such that the inequality (2) holds for all indexes e and f.

The following Theorems 1 and 2 have been proven in [54].

Theorem 1

([54]). There exists a J-solution $S\left(T\right)$ for the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with a fixed order $J_v\to J_w$ of the jobs $J_v$ and $J_w$ in all permutations ${\pi }_q$, $({\pi }_q,{\pi }_q) \in S\left(T\right)$, if and only if at least one of the following two conditions hold:

$$u_{v1}\le l_{v2} and u_{v1}\le l_{w1};$$

(3)

$$u_{w2}\le l_{w1} and u_{w2}\le l_{v2}.$$

(4)

Theorem 2 provides the necessary and sufficient conditions for existing a single-element J-solution $S\left(T\right)=\left\{({\pi }_q,{\pi }_q)\right\}$ for the uncertain flow-shop scheduling problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$. The partition $\mathcal{J}={\mathcal{J}}^0\cup {\mathcal{J}}^1\cup {\mathcal{J}}^2\cup {\mathcal{J}}^{*}$ of the set $\mathcal{J}={\mathcal{J}}_{1,2}$ is given, where

${\mathcal{J}}^0=\{J_i\in \mathcal{J}:u_{i1}\le l_{i2},u_{i2}\le l_{i1}\},$

${\mathcal{J}}^1=\{J_i\in \mathcal{J}:u_{i1}\le l_{i2},u_{i2}>l_{i1}\}=\{J_i\in \mathcal{J}\setminus {\mathcal{J}}^0:u_{i1}\le l_{i2}\},$

${\mathcal{J}}^2=\{J_i\in \mathcal{J}:u_{i1}>l_{i2},u_{i2}\le l_{i1}\}=\{J_i\in \mathcal{J}\setminus {\mathcal{J}}^0:u_{i2}\le l_{i1}\},$

${\mathcal{J}}^{*}=\{J_i\in \mathcal{J}:u_{i1}>l_{i2},u_{i2}>l_{i1}\}.$

Note that for each job $J_g\in {\mathcal{J}}^0$, the inequalities $u_{g1}\le l_{g2}$ and $u_{g2}\le l_{g1}$ imply the equalities $l_{g1}=u_{g1}=l_{g2}=u_{g2}$. Thus, the equalities $p_{g1}=p_{g2}=:p_g$ hold.

Theorem 2

([54]). There exists a single-element J-solution $S\left(T\right)\subset S$, $\left|S\right(T\left)\right|$$=1,$ for the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$, if and only if the following two conditions hold:

(j) for any pair of jobs $J_i$ and $J_j$ from the set ${\mathcal{J}}^1$ (from the set ${\mathcal{J}}^2$, respectively), either $u_{i1}\le l_{j1}$ or $u_{j1}\le l_{i1}$ (either $u_{i2}\le l_{j2}$ or $u_{j2}\le l_{i2}$, respectively);

(jj) inequality $|{\mathcal{J}}^{*}|\le 1$ holds and for the job $J_{i^{*}} \in {\mathcal{J}}^{*}$ both inequalities $l_{i^{*}1}\ge max\{u_{i1}:J_i \in {\mathcal{J}}^1\},$$l_{i^{*}2}\ge max\{u_{j2}:J_j \in {\mathcal{J}}^2\}$ hold with inequality $max\{l_{i^{*}1},l_{i^{*}2}\}\ge p_g$ valid for each job $J_g \in {\mathcal{J}}^0$.

Theorem 2 characterizes the simplest case of the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$, i.e., there is a job permutation ${\pi }_q$ dominating all others.

Let $\mathcal{J}\times \mathcal{J}$ denote a Cartesian product of the set $\mathcal{J}$. If ${\mathcal{J}}^0=\varnothing$, then there exists the following binary relation ${\mathcal{A}}_{\prec }\subseteq \mathcal{J}\times \mathcal{J}$ over the set $\mathcal{J}={\mathcal{J}}_{1,2}$.

Definition 2.

For the jobs $J_x \in \mathcal{J}$ and $J_y \in \mathcal{J}$, the inclusion $(J_x,J_y) \in {\mathcal{A}}_{\prec }$ holds if and only if at least one of the conditions (3) and (4) holds with $v=x$ and $w=y$ and neither the condition (3) no the condition (4) holds with $v=y$ and $w=x$ (or at least one of the conditions (3) and (4) holds both with $v=x$ and $w=y$ and with $v=y$, $w=x$ and $x<y$).

The above relation $(J_x,J_y) \in {\mathcal{A}}_{\prec }$ may be represented as follows: $J_x\prec J_y$. The binary relation ${\mathcal{A}}_{\prec }$ is a strict order [55] that determines the precedence digraph $\mathcal{G}=(\mathcal{J},{\mathcal{A}}_{\prec })$ with the vertex set $\mathcal{J}$ and the arc set ${\mathcal{A}}_{\prec }$. The permutation ${\pi }_q=(J_{q_1},J_{q_2},\dots ,J_{q_n})$, $({\pi }_q,{\pi }_q) \in S,$ is a total strict order over the set $\mathcal{J}$. The total strict order determined by the permutation ${\pi }_q$ is a linear extension of the partial strict order ${\mathcal{A}}_{\prec }$, if the inclusion $(J_{q_x},J_{q_y}) \in {\mathcal{A}}_{\prec }$ implies the inequality $x<y$. Let $\mathsf{\Pi }\left(\mathcal{G}\right)$ denote a set of all permutations ${\pi }_q \in S_{1,2}$ determining linear extensions of the partial strict order ${\mathcal{A}}_{\prec }$. The equality $\mathsf{\Pi }\left(\mathcal{G}\right)=\left\{{\pi }_q\right\}$ is characterized in Theorem 2, where the strict order ${\mathcal{A}}_{\prec }$ over the set $\mathcal{J}$ is represented as follows: $J_{q_1}\prec \dots \prec J_{q_i}\prec J_{q_{i+1}}\prec \dots \prec J_{q_n}.$ The following two claims have been proven in [55].

Theorem 3

([55]). For any scenario $p \in T$, the set $\mathsf{\Pi }\left(\mathcal{G}\right)$ contains a Johnson’s permutation for the deterministic flow-shop problem $F2\left|p\right|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_{1,2}={\mathcal{J}}^{*}\cup {\mathcal{J}}^1\cup {\mathcal{J}}^2$.

Corollary 1

([55]). There exists a J-solution $S\left(T\right)$ for the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_{1,2}={\mathcal{J}}^{*}\cup {\mathcal{J}}^1\cup {\mathcal{J}}^2$, such that the inclusion ${\pi }_q \in \mathsf{\Pi }\left(\mathcal{G}\right)$ holds for all pairs of job permutations, where $({\pi }_q,{\pi }_q) \in S\left(T\right)$.

In [55], it is shown how to determine a minimal dominant set $S\left(T\right)=\left\{({\pi }_q,{\pi }_q)\right\}$ with ${\pi }_q \in \mathsf{\Pi }\left(\mathcal{G}\right)$. The digraph $\mathcal{G}=(\mathcal{J},{\mathcal{A}}_{\prec })$ is considered as a condense form of a J-solution for the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$. The above results are used in Section 4, Section 5 and Section 6 for reducing a size of the dominant set $S\left(T\right)$ for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$.

4. The Off-Line Phase of Scheduling

The above setting of the uncertain job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le n|C_{max}$ implies the following remark.

Remark 3.

The factual value $p_{ij}^{*}$ of the job processing time $p_{ij}$ becomes known at the time-point $c_j\left(i\right)$ when the operation $O_{ij}$ is completed on the machine $M_j \in \mathcal{M}$.

Due to Remark 3, if all jobs $\mathcal{J}$ are completed on the corresponding machines from the set $\mathcal{M}$, the durations of all operations $O_{ij}$ take on exact values $p_{ij}^{*}$, where $l_{ij}\le p_{ij}^{*}\le u_{ij}$, and a unique factual scenario $p^{*} \in T$ is realized. A pair of job permutations selected for this realization should be optimal for scenario $p^{*}$. For constructing such an optimal pair of job permutations, we propose to implement two phases, namely: the off-line phase of scheduling and the on-line phase of scheduling.

The off-line phase is completed before starting a realization of the selected semi-active schedule. At the off-line phase, a scheduler knows the exact lower and upper bounds on the job processing times and the aim is to determine a minimal dominant set of the pairs of job permutations $({\pi }^{\prime },{\pi }^{″})$.

The on-line phase is started when the corresponding machine starts the processing of the first job in the selected schedule. At this phase, a scheduler can use an additional information on the job processing time, since for each operation $O_{ij}$, the exact value $p_{ij}^{*}$ of the processing time $p_{ij} \in T$ becomes known at the completion time $c_j\left(i\right)$ of this operation; see Remark 3.

We next consider the off-line phase of scheduling for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ and describe the sufficient conditions for existing a small dominant set of the semi-active schedules. Along with Definition 1, the following one is also used.

Definition 3.

A set of the pairs of job permutations $DS\left(T\right)\subseteq S$ is a dominant set for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$, if for each scenario $p \in T$ the set $DS\left(T\right)$ contains at least one optimal pair of job permutations for the individual deterministic job-shop problem $J2|p,n_i\le 2|C_{max}$ with scenario p.

Obviously, the J-solution is a dominant set for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. Before processing the set $\mathcal{J}$ of given jobs, a scheduler does not know the exact values of the job processing times. Nevertheless, it is needed to determine an optimal pair of permutations of the jobs $\mathcal{J}$ for their processing on the machines $\mathcal{M}=\{M_1,M_2\}$.

In Section 4.1, the sufficient conditions are presented for existing a pair of job permutations $({\pi }^{\prime },{\pi }^{″})$ such that the equality $DS\left(T\right)=\left\{({\pi }^{\prime },{\pi }^{″})\right\}$ holds. Section 4.2 contains the sufficient conditions allowing a scheduler to construct a semi-active schedule (if any), which dominates all other schedules in the set S. If a singleton $DS\left(T\right)=\left\{({\pi }^{\prime },{\pi }^{″})\right\}$ does not exist, a scheduler should construct partial strict orders $A_{\prec }^{1,2}$ and $A_{\prec }^{2,1}$ over set ${\mathcal{J}}_{1,2}$ and set ${\mathcal{J}}_{2,1}$; see Section 3.

4.1. Conditions for Existing a Single Optimal Pair of Job Permutations

The following conditions for existing an optimal pair of job permutations are proven in [8].

Theorem 4

([8]). If one of the following conditions either (5) or (6) holds:

$$\sum _{J_i\in {\mathcal{J}}_{1,2}}{u}_{i1}\le \sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2}{l}_{i2} and\sum _{J_i\in {\mathcal{J}}_{1,2}}{l}_{i2}\ge \sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_1}{u}_{i1},$$

(5)

$$\sum _{J_i\in {\mathcal{J}}_{2,1}}{u}_{i2}\le \sum _{J_i\in {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_1}{l}_{i1} and\sum _{J_i\in {\mathcal{J}}_{2,1}}{l}_{i1}\ge \sum _{J_i\in {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_2}{u}_{i2},$$

(6)

then any pair of permutations $({\pi }^{\prime },{\pi }^{″}) \in S$ is a singleton $DS\left(T\right)=\left\{({\pi }^{\prime },{\pi }^{″})\right\}$ for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_1\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}$.

Corollary 2

([8]). If the following inequality holds:

$$\sum _{J_j\in {\mathcal{J}}_{1,2}}{u}_{i1}\le \sum _{J_j\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2}{l}_{i2},$$

(7)

then the set $<\left\{{\pi }_{1,2}\right\},S_{2,1}>\subseteq S$, where ${\pi }_{1,2}$ is an arbitrary permutation in the set $S_{1,2}$, is a dominant set for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_1\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}$.

Corollary 3

([8]). If the following inequality holds: ${\sum }_{J_j\in {\mathcal{J}}_{2,1}}{u}_{i2}\le {\sum }_{J_j\in {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_1}{l}_{i1},$ then the set $<S_{1,2},\left\{{\pi }_{2,1}\right\}>$, where ${\pi }_{2,1}$ is an arbitrary permutation in the set $S_{2,1}$, is a dominant set for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_1\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}$.

In order to determine an optimal permutation for processing jobs from the set ${\mathcal{J}}_{2,1}$ (set ${\mathcal{J}}_{1,2}$, respectively), we consider the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{1,2}\subseteq \mathcal{J}$ and the machine route $(M_1,M_2)$, and that with the job set ${\mathcal{J}}_{2,1}\subseteq \mathcal{J}$ and the machine route $(M_2,M_1)$. The following theorem has been proven in [8].

Theorem 5

([8]). Let the set $S_{1,2}^{\prime }\subseteq S_{1,2}$ be a set of permutations from the dominant set for the flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{1,2}$, and the set $S_{2,1}^{\prime }\subseteq S_{2,1}$ be a set of permutations from the dominant set for the flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{2,1}$. Then the set $<S_{1,2}^{\prime },S_{2,1}^{\prime }>\subseteq S$ is a dominant set for the job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_1\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}$.

4.2. Precedence Digraphs Determining a Minimal Dominant Set of Schedules

Based on Remark 1, the off-line phase of scheduling for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ may be based on solving the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{1,2}$ and that with the job set ${\mathcal{J}}_{2,1}$. A criterion for the existence of a single-element J-solution for the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ is determined in Theorem 2.

In what follows, it is assumed that the equality ${\mathcal{J}}_{1,2}={\mathcal{J}}_{1,2}^1\cup {\mathcal{J}}_{1,2}^2\cup {\mathcal{J}}_{1,2}^{*}$ holds, i.e., ${\mathcal{J}}_{1,2}^0=\varnothing$. Using the results presented in Section 3, one can determine a binary relation $A_{\prec }^{1,2}$ for the uncertain flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{1,2}$. For the job set ${\mathcal{J}}_{1,2}$, the binary relation $A_{\prec }^{1,2}$ determines the digraph $G_{1,2}=({\mathcal{J}}_{1,2},A_{\prec }^{1,2})$ with the vertex set ${\mathcal{J}}_{1,2}$ and the arc set $A_{\prec }^{1,2}$.

Definition 4.

Two jobs $J_x\in {\mathcal{J}}_{1,2}$ and $J_y\in {\mathcal{J}}_{1,2}$, $x\ne y$, are conflict if they are not in the relation $A_{\prec }^{1,2}$, i.e., $(J_x,J_y)\notin A_{\prec }^{1,2}$ and $(J_y,J_x)\notin A_{\prec }^{1,2}$.

Due to Definition 2, for the conflict jobs $J_x\in {\mathcal{J}}_{1,2}$ and $J_y\in {\mathcal{J}}_{1,2}$, $x\ne y$, relations (3) and (4) do not hold for the case $v=x$ with $w=y$, nor for the case $v=y$ with $w=x$.

Definition 5.

The inclusion-minimal set ${\mathcal{J}}_x\subseteq {\mathcal{J}}_{1,2}$ of the jobs is called a conflict set of the jobs, if for any job $J_y\in {\mathcal{J}}_{1,2}\setminus {\mathcal{J}}_x$ either relation $(J_x,J_y)\in A_{\prec }^{1,2}$ or relation $(J_y,J_x)\in A_{\prec }^{1,2}$ holds for each job $J_x\in {\mathcal{J}}_x$.

There may exist several conflict sets in the set ${\mathcal{J}}_{1,2}$. Let the strict order $A_{\prec }^{1,2}$ for the flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{1,2}$ be represented as follows:

$$J_1\prec J_2\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec J_{k+r+2}\prec \dots \prec J_{m_{1,2}}.$$

(8)

Here, an optimal permutation for processing jobs from the set $\{J_1,J_2,\dots ,J_k\}$ (for jobs from the set $\{J_{k+r+1},J_{k+r+2},\dots ,J_{m_{1,2}}\}$) is as follows: $(J_1,J_2,\dots ,J_k)$ ($(J_{k+r+1},J_{k+r+2},\dots ,J_{m_{1,2}}),$ respectively). All jobs between braces in the presentation (8) constitute the conflict set of the jobs and they are in relation $A_{\prec }^{1,2}$ with any job located outside the braces. Due to Theorem 3, the set $\mathsf{\Pi }\left(G_{1,2}\right)$ of the permutations generated by the digraph $G_{1,2}$ includes an optimal permutation for each vector $p_{1,2}$ of the processing times of the jobs ${\mathcal{J}}_{1,2}$. Due to Corollary 1, the set $S_{1,2}\left(T\right)=\left\{({\pi }_{1,2},{\pi }_{1,2})\right\}$ with ${\pi }_{1,2} \in \mathsf{\Pi }\left(G_{1,2}\right)$ is a J-solution for the flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{1,2}$. Analogously, the set $S_{2,1}\left(T\right)=\left\{({\pi }_{2,1},{\pi }_{2,1})\right\}$ with ${\pi }_{2,1} \in \mathsf{\Pi }\left(G_{2,1}\right)$ is a J-solution for the problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{2,1}$. Due to Theorem 5, one can determine a dominant set for the job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$ as follows: $<\mathsf{\Pi }\left(G_{1,2}\right),\mathsf{\Pi }\left(G_{2,1}\right)>\subseteq S$; see Remark 1.

The following three theorems are proven in [8], where the notation $L_2:={\sum }_{J_j\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2}{l}_{j2}$ is used. These theorems allow a scheduler to reduce the cardinality of a dominant set for the uncertain job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$.

Theorem 6

([8]). Let the strict order $A_{\prec }^{1,2}$ over the set ${\mathcal{J}}_{1,2}={\mathcal{J}}_{1,2}^{*}\cup {\mathcal{J}}_{1,2}^1\cup {\mathcal{J}}_{1,2}^2$ be determined as follows: $J_1\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec \dots \prec J_{m_{1,2}}$. If the following inequality holds:

$$\sum _{i=1}^{k+r}{u}_{i1}\le L_2+\sum _{i=1}^k{l}_{i2},$$

(9)

then the set $S^{\prime }=<\left\{{\pi }_{1,2}\right\},\mathsf{\Pi }\left(G_{2,1}\right)>\subset S$, where ${\pi }_{1,2} \in \mathsf{\Pi }\left(G_{1,2}\right)$, is a dominant set for the job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_1\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}$.

Theorem 7

([8]). Let the partial strict order $A_{\prec }^{1,2}$ over the set ${\mathcal{J}}_{1,2}={\mathcal{J}}_{1,2}^{*}\cup {\mathcal{J}}_{1,2}^1\cup {\mathcal{J}}_{1,2}^2$ be determined as follows: $J_1\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec \dots \prec J_{m_{1,2}}$. If the inequality

$$u_{k+s,1}\le L_2+\sum _{i=1}^{k+s-1}(l_{i2}-u_{i1})$$

(10)

holds for each  $s \in \{1,2,\dots ,r\},$ then the set $S^{\prime }=< \left\{{\pi }_{1,2}\right\},S_{2,1} >$, where ${\pi }_{1,2}=(J_1,\dots ,J_{k-1},J_k,J_{k+1},$$J_{k+2},\dots ,J_{k+r},J_{k+r+1},\dots ,J_{m_{1,2}}) \in \mathsf{\Pi }\left(G_{1,2}\right)$, is a dominant set for the job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_1\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}$.

Theorem 8

([8]). Let the partial strict order $A_{\prec }^{1,2}$ over the set ${\mathcal{J}}_{1,2}={\mathcal{J}}_{1,2}^{*}\cup {\mathcal{J}}_{1,2}^1\cup {\mathcal{J}}_{1,2}^2$ have the form $J_1\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec \dots \prec J_{m_{1,2}}$. If the inequality

$$\sum _{i=r-s+2}^{r-s+1}{l}_{k+i,1}\ge \sum _{j=r-s+1}^r{u}_{k+j,2}$$

(11)

holds for each $s \in \{1,2,\dots ,r\}$, then the set $S^{\prime }=<\left\{{\pi }_{1,2}\right\},S_{2,1}>$, where ${\pi }_{1,2}=(J_1,\dots ,J_{k-1},J_k,J_{k+1},$$J_{k+2},\dots ,J_{k+r},J_{k+r+1},\dots ,J_{m_{1,2}}) \in \mathsf{\Pi }\left(G_{1,2}\right)$, is a dominant set for the job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}={\mathcal{J}}_1\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}$.

One can describe the analogs of Theorems 6–8 for reducing the cardinality of a dominant set for the job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ provided that for the flow-shop problem $F2|l_{ij}\le p_{ij}\le u_{ij}|C_{max}$ with the job set ${\mathcal{J}}_{2,1}$, there exists a partial strict order $A_{\prec }^{2,1}$ over the set ${\mathcal{J}}_{2,1}={\mathcal{J}}_{2,1}^{*}\cup {\mathcal{J}}_{2,1}^1\cup {\mathcal{J}}_{2,1}^2$ with the following form: $J_1\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec \dots \prec J_{m_{2,1}}$.

If the set $\{J_1,\dots ,J_k\}$ is empty in the constructed job permutation, then it is needed to check the conditions of Theorem 8. If the set $\{J_{k+r+1},\dots ,J_{m_{1,2}}\}$ is empty, then one needs to check the conditions of Theorem 7. Note that it is enough to test only one permutation for checking the conditions of Theorem 7 and only one permutation for checking the conditions of Theorem 8; see [8].

4.3. An Illustrative Example

To illustrate the above results, we consider Example 1 of the uncertain job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with eight jobs $\{J_1,J_2,\dots ,J_8\}=\mathcal{J}$. Let three jobs $J_1$, $J_2$ and $J_3$ have the machine route $(M_1,M_2)$, jobs $J_6$, $J_7$ and $J_8$ have the opposite machine route $(M_2,M_1)$, job $J_4$ and job $J_5$ have to be processed only on machine $M_1$ and machine $M_2$, respectively. The partition $\mathcal{J}={\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_1\cup {\mathcal{J}}_2$ is given, where ${\mathcal{J}}_{1,2}=\{J_1,J_2,J_3\}$, ${\mathcal{J}}_{2,1}=\{J_6,J_7,J_8\}$, ${\mathcal{J}}_1=\left\{J_4\right\}$ and ${\mathcal{J}}_2=\left\{J_5\right\}$. The lower and upper bounds on the job processing times are determined in

Table 1. The numerical input data for Example 1.

${\mathit{J}}_{\mathit{j}}$	${\mathit{J}}_1$	${\mathit{J}}_2$	${\mathit{J}}_3$	${\mathit{J}}_4$	${\mathit{J}}_5$	${\mathit{J}}_6$	${\mathit{J}}_7$	${\mathit{J}}_8$
$l_{i1}$	6	8	7	2	-	1	1	1
$u_{i1}$	7	9	9	3	-	3	3	3
$l_{i2}$	6	5	4	-	2	2	3	4
$u_{i2}$	7	6	5	-	3	4	4	4

.

To solve this uncertain job-shop scheduling problem, one need to determine an optimal pair $({\pi }^{\prime },{\pi }^{″})$ of permutations of the eight jobs for their processing on machine $M_1$ and machine $M_2$. These permutations ${\pi }^{\prime }$ and ${\pi }^{″}$ have the following forms: ${\pi }^{\prime }=({\pi }_{1,2},{\pi }_1,{\pi }_{2,1})$, ${\pi }^{″}=({\pi }_{2,1},{\pi }_2,{\pi }_{1,2})$.

It is necessary to find four permutations ${\pi }_{1,2}$, ${\pi }_{2,1}$, ${\pi }_1$ and ${\pi }_2$ of the jobs from the sets ${\mathcal{J}}_{1,2}$, ${\mathcal{J}}_{2,1}$, ${\mathcal{J}}_1$ and ${\mathcal{J}}_2$, respectively. The permutations ${\pi }_1$ and ${\pi }_2$ are determined as follows: ${\pi }_1=\left(J_4\right)$ and ${\pi }_2=\left(J_5\right)$.

We test the sufficient conditions given in Section 4.1. The conditions (5) of Theorem 4 do not hold. For testing the conditions (6) of Theorem 4, one can obtain the following relations:

$$\sum _{J_i\in {\mathcal{J}}_{2,1}}{u}_{i2}=u_{6,2}+u_{7,2}+u_{8,2}=4+4+4=12\le \sum _{J_i\in {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_1}{l}_{i1}=l_{1,1}+l_{2,1}+l_{3,1}+l_{4,1}=6+8+7+2=23,$$

$$\sum _{J_i\in {\mathcal{J}}_{2,1}}{l}_{i1}=l_{6,1}+l_{7,1}+l_{8,1}=1+1+1=3\ngeqq \sum _{J_i\in {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_2}{u}_{i2}=u_{1,2}+u_{2,2}+u_{3,2}+u_{5,2}=7+6+5+3=21.$$

It should be noted that the case when conditions of Theorem 4 hold was considered in [8].

As the first condition in (6) holds, due to Corollary 3, one can construct permutation ${\pi }_{2,1}=(J_6,J_7,J_8)$ by arranging the jobs from the set ${\mathcal{J}}_{2,1}$ in the increasing of their indexes.

For the jobs from the set ${\mathcal{J}}_{1,2}$, the partition ${\mathcal{J}}_{1,2}={\mathcal{J}}_{1,2}^1\cup {\mathcal{J}}_{1,2}^2\cup {\mathcal{J}}_{1,2}^{*}$ holds, where ${\mathcal{J}}_{1,2}^{*}=\left\{J_1\right\}$ and ${\mathcal{J}}_{1,2}^2=\{J_2,J_3\}$. The condition of Theorem 2 holds for these jobs. Therefore, the following optimal permutation: ${\pi }_{1,2}=(J_1,J_2,J_3)$ is determined.

Thus, there exists a pair of job permutations $({\pi }^{\prime },{\pi }^{″}),$ where ${\pi }^{\prime }=(J_1,J_2,J_3,J_4,J_6,J_7,J_8)$ and ${\pi }^{″}=(J_6,J_7,J_8,J_5,J_1,J_2,J_3)$, which is optimal for all possible scenarios $p \in T$. Hence, there exists a single-element dominant set $DS\left(T\right)=\left\{({\pi }^{\prime },{\pi }^{″})\right\}$ for Example 1 of the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the bounds on the job processing times given in Table 1.

The optimal semi-active schedule is constructed for Example 1 at the off-line phase of scheduling, despite of the uncertainty of the job processing times. Such an issue is called as STOP 1 in the scheduling algorithms developed in [8] and used in Section 6 of this paper.

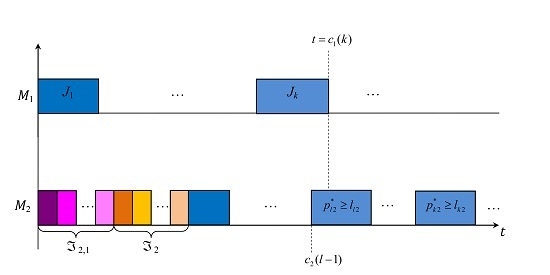
5. The On-line Phase of Scheduling

Due to Remark 3, if the job $J_i$ is completed on the corresponding machine $M_j\in \mathcal{M}$, the duration of the operation $O_{ij}$ takes on exact value $p_{ij}^{*}$, where $l_{ij}\le p_{ij}^{*}\le u_{ij}$. A scheduler can use this information on the duration of the operation $O_{ij}$ for a selection of the next job for processing on machine $M_j$. Since it is on-line phase of scheduling, such a selection should be very quick.

It is first assumed that the set $S^{\prime }=<\mathsf{\Pi }\left(G_{1,2}\right),\{{\pi }_{2,1}^{*}\}>\subset S$, is a dominant set for the problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$. In other words, the optimal permutations for processing all jobs from the set ${\mathcal{J}}_{2,1}$ are already determined at the off-line phase of scheduling.

Let the strict order $A_{\prec }^{1,2}$ over the set ${\mathcal{J}}_{1,2}={\mathcal{J}}_{1,2}^{*}\cup {\mathcal{J}}_{1,2}^1\cup {\mathcal{J}}_{1,2}^2$ be determined as follows: $J_1\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec \dots \prec J_{m_{1,2}}$. At the initial time $t=0$, machine $M_1$ has to start processing jobs from the set $\{J_1,\dots ,J_k\}$ in the following optimal order: $(J_1,\dots ,J_k)$. At the same time $t=0$, machine $M_2$ has to start processing jobs from the set ${\mathcal{J}}_{2,1}$ in the order determined by the permutation ${\pi }_{2,1}^{*}$, then jobs from the set ${\mathcal{J}}_2$ in the arbitrary order, and then jobs from the set $\{J_1,\dots ,J_k\}$ in the following optimal order: $(J_1,\dots ,J_k)$; see Figure 3.

At the time-point $t=c_1\left(k\right)$, machine $M_1$ completes the operation $O_{k1}$. Let $\mathcal{J}(i,j)$ denote a set of all jobs processed on machine $M_j$ from the initial part of the schedule till the job $J_i$, e.g., the set of jobs $\{J_1,J_2,\dots ,J_k\}$ is denoted as $\mathcal{J}(k,1)$; see Figure 3. Due to Remark 3, at the time-point $t=c_1\left(k\right)$, the factual values $p_{i1}^{*}$ of the processing times $p_{i1}$ of all jobs $J_i$ in the set $\mathcal{J}(k,1)$ are already known.

Let machine $M_2$ process the job $J_l\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup \{J_1,J_2,\dots ,J_k\}$ at the time-point $t=c_1\left(k\right)$, i.e., $t=c_1\left(k\right)<c_2\left(l\right)$. Let $\mathcal{J}(l-1,2)$ denote a set of all jobs whose processing is completed on machine $M_2$ before time-point $t=c_1\left(k\right)$. Figure 3 depicts this situation for the job $J_{l-1} \in \{J_1,J_2,\dots ,J_k\}\subset {\mathcal{J}}_{1,2}$.

The factual values $p_{i2}^{*}$ of the processing times $p_{i2}$ of all jobs $J_i$ in the set $\mathcal{J}(l-1,2)$ are known at the time-point $t=c_1\left(k\right)>c_2(l-1)$, i.e., $p_{i2}=p_{i2}^{*}$, while the factual values of the processing times $p_{j2}$ of other jobs in the set $\mathcal{J}$ remain unknown at the time-point $t=c_1\left(k\right)<c_2\left(l\right)$. Thus, at the time-point $t=c_1\left(k\right)$, the following subset of possible scenarios:

$$T(k,l-1)=\{p \in T:p_{i1}=p_{i1}^{*},p_{j2}=p_{j2}^{*},J_i \in \mathcal{J}(k,1),J_j \in \mathcal{J}(l-1,2)\}$$

may be realized instead of the initial set T of all possible scenarios; $T(k,l-1)\subseteq T$.

At the time-point $t=c_1\left(k\right)$ (it is called a decision-point), a scheduler has to make a decision about the order for processing jobs from the conflict set $\{J_{k+1},J_{k+2},\dots ,J_{k+r}\}$. The sufficient conditions given in Theorems 6 and 7 can be reformulated in the following two theorems. (Note that Theorem 8 cannot be reformulated for the use at the on-line phase of scheduling.)

Theorem 9.

Let the set $S^{\prime }=<\mathsf{\Pi }\left(G_{1,2}\right),\{{\pi }_{2,1}^{*}\}>\subset S$ be a dominant set for the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$. Let the strict order $A_{\prec }^{1,2}$ over the set ${\mathcal{J}}_{1,2}={\mathcal{J}}_{1,2}^{*}\cup {\mathcal{J}}_{1,2}^1\cup {\mathcal{J}}_{1,2}^2$ be determined as follows: $J_1\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec \dots \prec J_{m_{1,2}}$. If at the time-point $t=c_1\left(k\right)$, the following inequality holds:

$$c_1\left(k\right)+\sum _{i=k+1}^{k+r}{u}_{i1}\le c_2(l-1)+\sum _{J_i\in ({\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup \mathcal{J}(k,1))\setminus \mathcal{J}(l-1,2)}{l}_{i2},$$

(12)

then at the time-point $t=c_1\left(k\right)$, the set $S^{\prime }=<\left\{{\pi }_{1,2}\right\},\left\{{\pi }_{2,1}^{*}\right\}>\subset S$, where ${\pi }_{1,2} \in \mathsf{\Pi }\left(G_{1,2}\right)$, is a dominant set for the problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$ and the set $T(k,l-1)$ of possible scenarios.

Proof. 

Let p be an arbitrary vector from the set $T(k,l-1)$ of possible scenarios at the time-point $t=c_1\left(k\right)$. Let $C_{max}^p$ denote the optimal makespan value for the deterministic job-shop problem $J2|p,n_i\le 2|C_{max}$ with the set $\mathcal{J}$ of the given jobs and the vector p of the job processing times.

We consider an arbitrary permutation ${\pi }_{1,2} \in \mathsf{\Pi }\left(G_{1,2}\right)$ and show that the pair of job permutations $({\pi }^{\prime },{\pi }^{″})=(({\pi }_{1,2},{\pi }_1,{\pi }_{2,1}^{*}),$$({\pi }_{2,1}^{*},{\pi }_2,{\pi }_{1,2}))\in S^{\prime }$ is an optimal one for the deterministic job-shop problem $J2|p,n_i\le 2|C_{max}$ with the set $\mathcal{J}$ of the jobs and with any vector $p \in T(k,l-1)$ of the job processing times, i.e., the equality $C_{max}({\pi }^{\prime },{\pi }^{″})=C_{max}^p$ holds. Since the equality $C_{max}({\pi }^{\prime },{\pi }^{″})=max\{c_1\left({\pi }^{\prime }\right),c_2\left({\pi }^{″}\right)\}$ holds, one has to consider two possible cases (a) and (b).

Case (a): It is assumed that $c_1\left({\pi }^{\prime }\right)\ge c_2\left({\pi }^{″}\right).$ Then, one can obtain the following equalities:

$$C_{max}({\pi }^{\prime },{\pi }^{″})=c_1\left({\pi }^{\prime }\right)=max\{\sum _{J_i\in {\mathcal{J}}_{1,2}\cup {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_1}{p}_{i1},C_{max}({\pi }_{2,1}^{*})\},$$

(13)

where $C_{max}({\pi }_{2,1}^{*})$ is the value of makespan for the deterministic flow-shop problem $F2|p_{2,1}|C_{max}$ with the job set ${\mathcal{J}}_{2,1}$ and the vector $p_{2,1}$ whose components are equal to the corresponding components of the vector p. Due to the conditions of Theorem 9, the permutation ${\pi }_{2,1}^{*}$ is optimal for the deterministic flow-shop problem $F2|p_{2,1}|C_{max}$ with the set ${\mathcal{J}}_{2,1}$ of the given jobs and with vector $p_{2,1}$ of the job processing times. Therefore, $C_{max}({\pi }_{2,1}^{*})$ is an optimal makespan value for the deterministic flow-shop problem $F2|p_{2,1}|C_{max}$ and $C_{max}({\pi }_{2,1}^{*})$ is a minimal completion time for processing all jobs from the set ${\mathcal{J}}_{2,1}$ on both machines. From the equalities (13), one can obtain the equality $C_{max}({\pi }^{\prime },{\pi }^{″})=C_{max}^p$.

Case (b): It is assumed that $c_1\left({\pi }^{\prime }\right)<c_2\left({\pi }^{″}\right).$ Then, one can obtain the following equalities:

$$C_{max}({\pi }^{\prime },{\pi }^{″})=c_2\left({\pi }^{″}\right)=max\{\sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}}{p}_{i2},C_{max}\left({\pi }_{1,2}\right)\},$$

(14)

where $C_{max}\left({\pi }_{1,2}\right)$ is an optimal value of the makespan criterion for the deterministic flow-shop problem $F2|p_{1,2}|C_{max}$ with the job set ${\mathcal{J}}_{1,2}$ and with the vector $p_{1,2}$ of the job processing times (the components of this vector are equal to the corresponding components of the vector p). Since ${\pi }_{1,2} \in \mathsf{\Pi }\left(G_{1,2}\right)$, the initial part of the permutation ${\pi }_{1,2}$ has the following form: $(J_1,J_2,\dots ,J_k).$ For every pair of jobs from the set $\{J_1,J_2,\dots ,J_k\}$, at least one of the conditions, either (3) or (4), holds, see Theorem  1.

Therefore, for the job processing times determined by the vector p for the jobs $\{J_1,J_2,\dots ,J_k\}$, the inequalities (2) hold. Thus, in the permutation ${\pi }_{1,2}^{beg}:=(J_1,J_2,\dots ,J_k)$, all the jobs are arranged in the Johnson’s order. One can conclude that the following value

$$C_{max}\left({\pi }_{1,2}^{beg}\right)=\underset{1\le m\le k}{max}\{\sum _{i=1}^m{p}_{i1}+\sum _{i=m}^k{p}_{i2}\}$$

(15)

determines an optimal makespan value for the deterministic flow-shop problem $F2|p_{1,2}^{beg}|C_{max}$ with the job set $\{J_1,J_2,\dots ,J_k\}$ and the corresponding vector $p_{1,2}^{beg}$ of the job processing times (the components of the vector $p_{1,2}^{beg}$ are equal to the corresponding components of the vector p). Therefore, $C_{max}\left({\pi }_{1,2}^{beg}\right)$ is a minimal makespan value for processing jobs of the set $\{J_1,J_2,\dots ,J_k\}$ on both machines. Then, for the time-point $c_2\left(k\right)$ when machine $M_2$ completes the operation $O_{k2}$, one can obtain the following equality:

$$c_2\left(k\right)=max\{\sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}(k,1)}{p}_{i2},C_{max}({\pi }_{1,2}^{beg})\}.$$

(16)

Due to the inequality (12) and the equality (16), one can obtain the following inequalities for the jobs from the conflict set $\{J_{k+1},J_{k+2},\dots ,J_{k+r}\}$:

$$c_1\left(k\right)+\sum _{i=k+1}^{k+r}{p}_{i1}\le c_1\left(k\right)+\sum _{i=k+1}^{k+r}{u}_{i1}\le c_2(l-1)+\sum _{J_i\in ({\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup \mathcal{J}(k,1))\setminus \mathcal{J}(l-1,2)}{l}_{i2}\le$$

(17)

$$\le c_2(l-1)+\sum _{J_i\in ({\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup \mathcal{J}(k,1))\setminus \mathcal{J}(l-1,2)}{p}_{i2}\le max\{\sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}(k,1)}{p}_{i2},C_{max}\left({\pi }_{1,2}^{beg}\right)\}=c_2\left(k\right).$$

From the inequalities (17), one can obtain the following inequality:

$$c_1\left(k\right)+\sum _{i=k+1}^{k+r}{p}_{i1}\le c_2\left(k\right).$$

(18)

Thus, machine $M_2$ processes all jobs from the conflict set $\{J_{k+1},J_{k+2},\dots ,J_{k+r}\}$ without idle times and without an idle before processing the first job from this conflict set for any order of these conflict jobs. Using the inequality (18), one can conclude that the time-point when machine $M_2$ completes the processing of the last job from the conflict set $\{J_{k+1},J_{k+2},\dots ,J_{k+r}\}$ in the permutation ${\pi }_{1,2}$ is determined as follows:

$$c_2=c_2\left(k\right)+\sum _{i=k+1}^{k+r}{p}_{i2},$$

(19)

where $c_2$ is an optimal makespan value for processing jobs from the set $\{J_1,J_2,\dots ,J_k,J_{k+1},$$J_{k+2},\dots ,J_{k+r}\}.$ Next, we consider jobs from the set $\{J_{k+r+1},\dots ,J_{m_{1,2}}\}.$

Let ${\pi }_{1,2}^{end}:=(J_{k+r+1},\dots ,J_{m_{1,2}})$ denote the permutation of the jobs $\{J_{k+r+1},\dots ,J_{m_{1,2}}\}$ in the permutation ${\pi }_{1,2}$. Analogously as for the job set $\{J_1,J_2,\dots ,J_k\}$, one can obtain that the value of

$$C_{max}\left({\pi }_{1,2}^{end}\right):=\underset{k+r+1\le m\le m_{1,2}}{max}\{\sum _{i=k+r+1}^m{p}_{i1}+\sum _{i=m}^{m_{1,2}}{p}_{i2}\}$$

(20)

is an optimal makespan value for the deterministic flow-shop problem $F2|p_{1,2}^{end}|C_{max}$ with the job set $\{J_{k+r+1},\dots ,J_{m_{1,2}}\}$ and with the vector $p_{1,2}^{end}$ whose components are equal to the components of the vector p. Thus, $C_{max}\left({\pi }_{1,2}^{end}\right)$ is a minimal makespan value for processing all jobs from the set $\{J_{k+r+1},\dots ,J_{m_{1,2}}\}$ on both machines. The time-point when machine $M_2$ completes the processing of the last job from the permutation ${\pi }^{″}$ can be calculated as follows:

$$c_2\left({\pi }^{″}\right)=max\{\sum _{i=1}^{k+r}{p}_{i1}+C_{max}\left({\pi }_{1,2}^{end}\right),c_2+\sum _{i=k+r+1}^{m_{1,2}}{p}_{i2}\}=$$

$$=max\{\sum _{i=1}^{k+r}{p}_{i1}+C_{max}\left({\pi }_{1,2}^{end}\right),c_2\left(k\right)+\sum _{i=k+1}^{k+r}{p}_{i2}+\sum _{i=k+r+1}^{m_{1,2}}{p}_{i2}\}=$$

$$=max\{\sum _{i=1}^{k+r}{p}_{i1}+C_{max}\left({\pi }_{1,2}^{end}\right),max\{\sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}(k,1)}{p}_{i2},C_{max}\left({\pi }_{1,2}^{beg}\right)\}+\sum _{i=k+1}^{m_{1,2}}{p}_{i2}\}=$$

$$=max\{\sum _{i=1}^{k+r}{p}_{i1}+C_{max}\left({\pi }_{1,2}^{end}\right),\sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}(k,1)}{p}_{i2}+\sum _{i=k+1}^{m_{1,2}}{p}_{i2},C_{max}\left({\pi }_{1,2}^{beg}\right)+\sum _{i=k+1}^{m_{1,2}}{p}_{i2}\}=$$

$$=max\{C_{max}\left({\pi }_{1,2}^{beg}\right)+\sum _{i=k+1}^{m_{1,2}}{p}_{i2},\sum _{i=1}^{k+r}{p}_{i1}+C_{max}\left({\pi }_{1,2}^{end}\right),\sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}}{p}_{i2}\},$$

(21)

where relations (16) and (19) are used.

Due to Theorem 3, the set $\mathsf{\Pi }\left(G_{1,2}\right)$ contains a Johnson’s permutation for the deterministic flow-shop problem $F2|p_{1,2}|C_{max}$ with the job set ${\mathcal{J}}_{1,2}$ and with the vector $p_{1,2}$ of the job durations. We denote this Johnson’s permutation as ${\pi }_{1,2}^{*}$. Since ${\pi }_{1,2}^{*} \in \mathsf{\Pi }\left(G_{1,2}\right)$, the permutation ${\pi }_{1,2}^{*}$ has the following form: ${\pi }_{1,2}^{*}=(J_1,\dots ,J_k,J_{[k+1]},J_{[k+2]},\dots ,J_{[k+r]},J_{k+r+1},\dots ,J_{m_{1,2}}),$ where the set of indexes is determined as follows: $\left\{\right[k+1],[k+2],\dots ,[k+r\left]\right\}=\{k+1,k+2,\dots ,k+r\}$.

The optimal makespan value $C_{max}\left({\pi }_{1,2}^{*}\right)$ can be calculated as follows:

$$C_{max}\left({\pi }_{1,2}^{*}\right)=\underset{1\le m\le m_{1,2}}{max}\{\sum _{i=1}^m{p}_{i1}+\sum _{i=m}^{m_{1,2}}{p}_{i2}\}=max\{\underset{1\le m\le k}{max}\{\sum _{i=1}^m{p}_{i1}+\sum _{i=m}^k{p}_{i2}+\sum _{i=k+1}^{m_{1,2}}{p}_{i2}\},$$

$$\underset{[k+1]\le m\le [k+r]}{max}\{\sum _{i=1}^m{p}_{i1}+\sum _{i=m}^{m_{1,2}}{p}_{i2}\},\underset{k+r+1\le m\le m_{1,2}}{max}\{\sum _{i=1}^{k+r}{p}_{i1}+\sum _{i=k+r+1}^m{p}_{i1}+\sum _{i=m}^{m_{1,2}}{p}_{i2}\}\}=$$

$$=max\{C_{max}\left({\pi }_{1,2}^{beg}\right)+\sum _{i=k+1}^{m_{1,2}}{p}_{i2},\underset{[k+1]\le m\le [k+r]}{max}\{\sum _{i=1}^m{p}_{i1}+\sum _{i=m}^{m_{1,2}}{p}_{i2}\},\sum _{i=1}^{k+r}{p}_{i1}+C_{max}\left({\pi }_{1,2}^{end}\right)\},$$

(22)

where relations (15) and (20) are used. From relations (21) and (22), one can obtain the relations

$$c_2\left({\pi }^{″}\right)=max\{C_{max}\left({\pi }_{1,2}^{beg}\right)+\sum _{i=k+1}^{m_{1,2}}{p}_{i2},\sum _{i=1}^{k+r}{p}_{i1}+C_{max}\left({\pi }_{1,2}^{end}\right),\sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}}{p}_{i2}\}\le$$

$$\le max\{C_{max}\left({\pi }_{1,2}^{*}\right),\sum _{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup {\mathcal{J}}_{1,2}}{p}_{i2}\}.$$

(23)

Therefore, relations (14) and (23) imply the equality $C_{max}({\pi }^{\prime },{\pi }^{″})=C_{max}^p$.

Thus, in both cases (a) and (b), the equality $C_{max}({\pi }^{\prime },{\pi }^{″})=C_{max}^p$ holds and the pair of permutations $({\pi }^{\prime },{\pi }^{″})=(({\pi }_{1,2},{\pi }_1,{\pi }_{2,1}^{*}),({\pi }_{2,1}^{*},{\pi }_2,{\pi }_{1,2}))$ is optimal for the deterministic job-shop problem $J2|p,n_i\le 2|C_{max}$ with the scenario $p \in T(k,l-1)$. Therefore, the set $S^{\prime }=<\left\{{\pi }_{1,2}\right\},\{{\pi }_{2,1}^{*}\}>$ contains an optimal pair of job permutations for the job-shop problem $J2|p,n_i\le 2|C_{max}$ with vector $p \in T(k,l-1)$ of the job processing times. Since the vector p is arbitrarily chosen in the set $T(k,l-1)$, the set $S^{\prime }$ contains an optimal pair of job permutations for each scenario in the set $T(k,l-1)$.

Due to Definition 3, the set $S^{\prime }$ is a dominant set for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$ and with the set $T(k,l-1)$ of possible scenarios. □

Theorem 10.

Let the set $S^{\prime }=<\mathsf{\Pi }\left(G_{1,2}\right),\{{\pi }_{2,1}^{*}\}>\subset S$ be a dominant set for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$. Let the partial strict order $A_{\prec }^{1,2}$ over the set ${\mathcal{J}}_{1,2}={\mathcal{J}}_{1,2}^{*}\cup {\mathcal{J}}_{1,2}^1\cup {\mathcal{J}}_{1,2}^2$ be determined as follows: $J_1\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec \dots \prec J_{m_{1,2}}$. If at the time-point $t=c_1\left(k\right)$, the following inequalities hold:

$$c_1\left(k\right)+\sum _{i=k+1}^{k+s}{u}_{i1}\le c_2(l-1)+\sum _{J_i\in ({\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup \mathcal{J}(k-1,1))\setminus \mathcal{J}(l-1,2)}{l}_{i2}+\sum _{i=k}^{k+s-1}{l}_{i2}$$

(24)

for all indexes $s \in \{1,2,\dots ,r\},$ then at the time-point $t=c_1\left(k\right)$, the set $S^{\prime }=<\left\{{\pi }_{1,2}\right\},\{{\pi }_{2,1}^{*}\}>$, where ${\pi }_{1,2}=(J_1,\dots ,J_{k-1},J_k,$$J_{k+1},J_{k+2},\dots ,J_{k+r},$$J_{k+r+1},\dots ,J_{m_{1,2}}) \in \mathsf{\Pi }\left(G_{1,2}\right)$, is a dominant set for the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$ and the set $T(k,l-1)$ of possible scenarios.

Proof. 

The proof of this theorem is similar to the above proof of Theorem 9 with the exception of the inequalities (17) and (18). From the condition (24) with $s=1$, one can obtain the following inequality:

$$c_1\left(k\right)+u_{k+1,1}\le c_2(l-1)+\sum _{J_i\in ({\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup \mathcal{J}(k-1,1))\setminus \mathcal{J}(l-1,2)}{l}_{i2}+l_{k2}.$$

(25)

Based on the inequality (25), one can obtain the following relations:

$$c_1\left(k\right)+p_{k+1,1}\le c_1\left(k\right)+u_{k+1,1}\le c_2(l-1)+\sum _{J_i\in ({\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup \mathcal{J}(k-1,1))\setminus \mathcal{J}(l-1,2)}{l}_{i2}+l_{k2}\le$$

$$\le c_2(l-1)+\sum _{J_i\in ({\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2\cup \mathcal{J}(k,1))\setminus \mathcal{J}(l-1,2)}{p}_{i2}=c_2\left(k\right).$$

(26)

Due to relations (26), the following inequality holds:

$$c_1\left(k\right)+p_{k+1,1}\le c_2\left(k\right).$$

(27)

Thus, machine $M_2$ processes the job $J_{k+1}$ in permutation ${\pi }_{1,2}$ without an idle time between the jobs $J_k$ and $J_{k+1}$. Analogously, using $s \in \{2,3,\dots ,r\}$, one can show that the following inequalities hold:

$$c_1\left(k\right)+p_{k+1,1}+p_{k+2,1}\le c_2(k+1);$$

$$c_1\left(k\right)+p_{k+1,1}+p_{k+2,1}+p_{k+3,1}\le c_2(k+2);$$

$$\cdots ;$$

$$c_1\left(k\right)+\sum _{i=k+1}^{k+r}{p}_{i1}\le c_2(k+r-1).$$

Therefore, machine $M_2$ processes jobs from the conflict set $\{J_{k+1},J_{k+2},\dots ,J_{k+r}\}$ in permutation ${\pi }_{1,2}$ without idle times between the jobs $J_{k+1}$ and $J_{k+2}$, between the jobs $J_{k+2}$ and $J_{k+3}$ and so on, between the jobs $J_{k+r-1}$ and $J_{k+r}$. Then, the following relations hold:

$$c_2=c_2(k+r)=c_2(k+r-1)+p_{k+r,2}=c_2(k+r-2)+p_{k+r-1,2}+p_{k+r,2}=\dots =c_2\left(k\right)+\sum _{i=k+1}^{k+r}{p}_{i2}$$

leading to the equality (19). The rest of the proof is the same as the rest of the proof of Theorem 9.

It is shown that the pair of job permutations $({\pi }^{\prime },{\pi }^{″})=(({\pi }_{1,2},{\pi }_1,{\pi }_{2,1}^{*}),$ $({\pi }_{2,1}^{*},{\pi }_2,{\pi }_{1,2})) \in S^{\prime }$ is optimal for the deterministic job-shop problem $J2|p,n_i\le 2|C_{max}$ with any vector $p \in T(k,l-1)$ of the job processing times. Due to Definition 3, the set $S^{\prime }$ is a dominant set for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$ and the set $T(k,l-1)$ of possible scenarios. □

It is easy to be convinced that the sufficient conditions given in Theorems 9 and 10 may be tested in polynomial time $O\left(r^2\right)$ of the number r of the conflict jobs.

Similarly, one can prove analogs of Theorems 9 and 10 if the set $S^{\prime }=<\{{\pi }_{1,2}^{*}\},\mathsf{\Pi }\left(G_{2,1}\right)>\subset S$ provided that a dominant set for the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the job set $\mathcal{J}$ and the partial strict order $A_{\prec }^{2,1}$ over the set ${\mathcal{J}}_{2,1}={\mathcal{J}}_{2,1}^{*}\cup {\mathcal{J}}_{2,1}^1\cup {\mathcal{J}}_{2,1}^2$ has the following form: $J_1\prec \dots \prec J_k\prec \{J_{k+1},J_{k+2},\dots ,J_{k+r}\}\prec J_{k+r+1}\prec \dots \prec J_{m_{2,1}}$.

6. Scheduling Algorithms and Computational Results

The experimental study was performed on a large number of randomly generated instances of the uncertain job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. The off-line phase of scheduling was based on Algorithms 1 and 2 developed in [8]. Algorithms 1 and 2 are presented in Appendix A.

Algorithms 3–5 are developed for the on-line phase of scheduling. The input for each of these three algorithms includes the output of Algorithms 1 and 2 [8] applied at the off-line phase of scheduling.

Let outputs of Algorithms 1 and 2 [8] applied at the off-line phase of scheduling consist of the optimal permutation ${\pi }_{1,2}$ of the jobs ${\mathcal{J}}_{1,2}$ and the optimal permutation ${\pi }_{2,1}$ of the jobs ${\mathcal{J}}_{2,1}$. In such a case, the single-element dominant set $DS\left(T\right)=\{({\pi }_{1,2},{\pi }_1,{\pi }_{2,1}),({\pi }_{2,1},{\pi }_2,{\pi }_{1,2})\}$ is already constructed for the considered instance of the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. Therefore, the pair $\{({\pi }_{1,2},{\pi }_1,{\pi }_{2,1}),({\pi }_{2,1},{\pi }_2,{\pi }_{1,2})\}$ of the job permutations is optimal for the deterministic instance $J2|p,n_i\le 2|C_{max}$ with any scenario $p \in T$. Thus, such an instance of the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ is optimally solved by Algorithms 1 and 2 at the off-line phase of scheduling. Hence, there is no need to use the on-line phase of scheduling for such an instance of the uncertain job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$.

In Section 6.1, it shown how to solve instances of the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$, which cannot be optimally solved at the off-line phase of scheduling.

6.1. Algorithms 3–5 for the On-Line Phase of Scheduling

Let the considered instance of the uncertain job-shop problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ cannot be optimally solved by Algorithms 1 and 2 [8] applied at the off-line phase of scheduling. Thus, due to an application of Algorithm 1 or Algorithm 2, one can obtain one of the following three possible outputs:

(a)

the permutation ${\pi }_{2,1}$ of the jobs from set ${\mathcal{J}}_{2,1}$ and the partial strict order $A_{\prec }^{1,2}$ of the jobs ${\mathcal{J}}_{1,2}$;

(b)

the permutation ${\pi }_{1,2}$ of the jobs from set ${\mathcal{J}}_{1,2}$ and the partial strict order $A_{\prec }^{2,1}$ of the jobs ${\mathcal{J}}_{2,1}$;

(c)

the partial strict order $A_{\prec }^{1,2}$ of the jobs ${\mathcal{J}}_{1,2}$ and the partial strict order $A_{\prec }^{2,1}$ of the jobs ${\mathcal{J}}_{2,1}$.

Let B denote a number of the conflict sets in a partial strict order (in both partial strict orders) for the obtained output (a), (b) or (c). In other words, B denotes a maximal number of time-points in the decision-making at the on-line phase of scheduling. Let integer b, where $b\le B,$ denote a number of time-points in the decision-making, where optimal orders of the conflict jobs were found using Theorem 9 or Theorem 10. Using these notations, we next describe Algorithm 3 provided that there is no factual processing times of the jobs $\mathcal{J}$ in the input of Algorithm 3; see Remark 3.

Let Algorithm 3 terminate at Step 16, i.e., it has not been constructed an optimal pair of job permutations for the factual scenario $p^{*} \in T$ randomly determined after completing the on-line phase of scheduling. Therefore, there is a strictly positive error $\Delta \left(s\right)$ of the objective function $C_{max}\left(s\right)$ calculated for the constructed and realized schedule s. In such a case, the proven sufficient conditions for the optimality of the schedule s do not hold in some decision-points (or in a single decision-point) at the on-line phase of scheduling. If Algorithm 3 terminates at Step 17, then an optimal pair of job permutations has been constructed for the factual scenario $p^{*} \in T$ randomly generated after completing the on-line phase of scheduling. The optimality of this pair of the job permutations was established only after the schedule execution, since the tested sufficient conditions for the optimality of the schedule s do not hold in some decision-points (or in a single decision-point).

If Algorithm 3 terminates at Step 18, then the tested sufficient conditions hold for all decision-points considered at the on-line phase of scheduling. Therefore, the constructed pair of job permutations is optimal for all factual scenarios $p^{*} \in T$ which were possible during the on-line phase of scheduling. In this case, the optimal pair of job permutations was established before the end of the schedule execution (after the last decision-point). The described Algorithm 3 must be used if the input (a) is obtained due to the application of Algorithms 1 and 2 [8] at the off-line phase of scheduling. Similarly, one can describe Algorithm 4 with the sufficient conditions from the analogs of Theorems 9 and  10 for their use in the case, when the input (b) is obtained due to the application of Algorithms 1 and 2 at the off-line phase of scheduling.

Similar Algorithm 5 must be used in the case, when the input (c) is obtained due to the application of Algorithms 1 and 2 at the off-line phase of scheduling. In Algorithm 3, a decision-point may occur on machine $M_1$ and on machine $M_2$ simultaneously. Therefore, one has to check the conditions of Theorems 9 and 10 or their analogs alternately for the corresponding conflict sets of the jobs from the set ${\mathcal{J}}_{1,2}$ and those from the set ${\mathcal{J}}_{2,1}$.

Algorithm 3 for the on-line phase of scheduling
Input:	Lower bounds $l_{ij}$ and upper bounds $u_{ij}$ on the durations $p_{ij}$ of all operations $O_{ij} \in \mathcal{J}$ processed on machines $M_j \in \mathcal{M}$; a permutation ${\pi }_1$ of the jobs ${\mathcal{J}}_1$ and a permutation ${\pi }_2$ of the jobs ${\mathcal{J}}_2$; an optimal permutation ${\pi }_{2,1}$ of the jobs from the set ${\mathcal{J}}_{2,1}$; a partial strict order $A_{\prec }^{1,2}$ of the jobs from the set ${\mathcal{J}}_{1,2}$; a number B of the conflict sets in the partial strict order $A_{\prec }^{1,2}$.
Output:	Permutation ${\pi }_{1,2}$ of the jobs from the set ${\mathcal{J}}_{1,2}$.
Step 1:	Set $b=0$.
Step 2:	UNTIL the completion time-point of the last job in the set $\mathcal{J}$,  process the whole linear part of the jobs in the partial strict order $A_{\prec }^{1,2}$   on the machine $M_1$ till a conflict set of the jobs is met;  let t denote a time-point of the completion of the linearly ordered set of jobs.
Step 3:	Process jobs of the permutation $({\pi }_{2,1},{\pi }_2)$ and then process the linear part  in the partial strict order $A_{\prec }^{1,2}$ on the machine $M_2$ up to time-point t.
Step 4:	Check the conditions of Theorem 9 for the conflict set of the jobs.
Step 5:	IF the sufficient conditions of Theorem 9 hold  THEN set $b:=b+1$ and choose an arbitrary order ${\pi }_q$ of the conflict jobs  GOTO step 11.
Step 6:	ELSE set $d_z=l_{z2}-u_{z1}$ for all conflict jobs $J_z$  and partition the conflict jobs $J_z$ into two subsets $X_1$ and $X_2$,  where $J_z \in X_1$ if $d_z\ge 0$, and $J_z \in X_2$ otherwise.
Step 7:	Construct the following order ${\pi }_q$ of the conflict jobs:  First, arrange the jobs from the set $X_1$ in the non-decreasing order   of the values of $u_{i1}$, then arrange the jobs from the set $X_2$   in the non-increasing order of the values of $l_{i2}$.
Step 8:	Check the conditions of Theorem 10 for the constructed  permutation of the conflict jobs.
Step 9:	IF the sufficient conditions of Theorem 10 hold THEN  set $b:=b+1$ GOTO step 11.
Step 10:	Construct a Johnson’s permutation ${\pi }_q$ of the conflict jobs  based on the inequalities (2) provided that $p_{ij}=(u_{ij}+l_{ij})/2$.
Step 11:	Include the permutation ${\pi }_q$ of the conflict jobs in the strict order  $A_{\prec }^{1,2}$ instead of the conflict set of these jobs.
Step 12:	RETURN
Step 13:	IF$b=B$THEN GOTO step 18.
Step 14:	Calculate makespan $C_{max}\left(s\right)$ for the schedule s constructed at steps 1 – 12;  calculate makespan $C_{max}\left(s^{*}\right)$ for the optimal schedule $s^{*}$ polynomially  calculated for the corresponding deterministic problem $J2|p^{*},n_i\le 2|C_{max}$,  where the factual processing times $p^{*}$ are randomly generated for all jobs $\mathcal{J}$.
Step 15:	IF$C_{max}\left(s\right)$ = $C_{max}\left(s^{*}\right)$ THEN GOTO step 17.
Step 16:	STOP 4: The constructed schedule s is not optimal for the factual  processing times $p^{*}$ of the jobs $\mathcal{J}$.
Step 17:	STOP 3: The optimality of the constructed schedule s for the factual  processing times $p^{*}$ of the jobs $\mathcal{J}$ was established only after  the execution of the schedule s.
Step 18:	STOP 2: The optimality of the constructed schedule s for the factual  processing times $p^{*}$ of the jobs $\mathcal{J}$ was proven before the end  of the execution of this schedule.

6.2. The Modified Example with Different Factual Scenarios

To demonstrate the on-line phase of scheduling based on Algorithm 3, it is considered Example 2 of the problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with the numerical input data given in Table 1 similarly as for Example 1 with the only one exception. It is assumed that $u_{3,2}=6$.

The first part of the off-line phase of scheduling for solving Example 2 is similar to that for Example 1 till checking the conditions of Theorem 2. Indeed, the conditions of Theorem 2 do not hold for the jobs from the set ${\mathcal{J}}_{1,2}$ since the following strict inequalities hold: $u_{2,2}>l_{3,2}$ and $u_{3,2}>l_{2,2}$.

Due to checking the inequalities (3) and (4), one can determine the binary relation $A_{\prec }^{1,2}$ over the set ${\mathcal{J}}_{1,2}$ in the following form: $J_1\prec \{J_2,J_3\}$. Thus, the set $\{J_2,J_3\}$ is a conflict set with two jobs; see Definition 5. Then, one can consecutively check the conditions of Theorems 6–8 for the jobs from the set ${\mathcal{J}}_{1,2}$. After letting $k=1$, $r=2$, one can calculate $L_2={\sum }_{J_i\in {\mathcal{J}}_{2,1}\cup {\mathcal{J}}_2}{l}_{i2}=l_{6,2}+l_{7,2}+l_{8,2}+l_{5,2}=2+3+4+2=11$ and then obtain the following relations:

$$\sum _{i=1}^{k+r}{u}_{i1}=u_{1,1}+u_{2,1}+u_{3,1}=7+9+9=25\nleqq L_2+\sum _{i=1}^k{l}_{i2}=L_2+l_{1,2}=11+6=17.$$

Thus, the condition of Theorem 6 does not hold for Example 2. Next, one can check the conditions of Theorem 7. Similarly as in the previous case, one can obtain that $L_2=11$, $k=1$, and $r=2$. Due to the condition (10), one can obtain two inequalities as follows: $s=1$ and $s=2$. Then, one can check both permutations of the jobs from the set ${\mathcal{J}}_{1,2}$, which satisfy the partial strict order $A_{\prec }^{1,2}$, as follows: $\mathsf{\Pi }\left({\mathcal{G}}_{1,2}\right)=\{{\pi }_{1,2}^1,{\pi }_{1,2}^2\}$, where ${\pi }_{1,2}^1=\{J_1,J_2,J_3\}$ and ${\pi }_{1,2}^2=\{J_1,J_3,J_2\}$.

Thus, the permutation ${\pi }_{1,2}^1$ must be tested. One can obtain the following relations:

$$u_{2,1}=9\le L_2+(l_{1,2}-u_{1,1})=11+(6-7)=10;$$

$$u_{3,1}=9\nleqq L_2+\sum _{i=1}^2(l_{i2}-u_{i1})=L_2+(l_{1,2}-u_{1,1})+(l_{2,2}-u_{2,1})=11+(6-7)+(5-9)=6.$$

Hence, the condition of Theorem 7 does not hold for the permutation ${\pi }_{1,2}^1$.

Analogously, for the permutation ${\pi }_{1,2}^2$, the following relations hold:

$$u_{3,1}=9\le L_2+(l_{1,2}-u_{1,1})=11+(6-7)=10;$$

$$u_{2,1}=9\nleqq L_2+\sum _{i=1}^2(l_{i2}-u_{i1})=L_2+(l_{1,2}-u_{1,1})+(l_{3,2}-u_{3,1})=11+(6-7)+(4-9)=5.$$

Hence, the condition of Theorem 7 does not hold for the permutation ${\pi }_{1,2}^2$ as well.

It is impossible to check the condition of Theorem 8, since the conflict set of the jobs $\{J_2,J_3\}$ is located at the end of the partial strict order $A_{\prec }^{1,2}$. Thus, the off-line phase of scheduling is completed, and the constructed partial strict order $A_{\prec }^{1,2}$ is not a linear order. Therefore, there does not exist a pair of permutations of the jobs, which is optimal for any scenario $p \in T$. In this case, Algorithms 1 and 2 [8] do not terminate with STOP 1. A scheduler needs to use the on-line phase of scheduling for solving Example 2 further.

The output of the off-line phase of scheduling for Example 2 contains the permutation ${\pi }_{2,1}=(J_6,J_7,J_8)$ of the jobs ${\mathcal{J}}_{2,1}$ processed on both machines $M_1$ and $M_2$. The partial strict order $A_{\prec }^{1,2}=(J_1\prec \{J_2,J_3\})$ of the jobs ${\mathcal{J}}_{1,2}$ is constructed. The obtained output (a) of the off-line phase of scheduling shows that Algorithm 3 must be used at the on-line phase of scheduling for solving Example 2.

We next show that Algorithm 3 can be stopped either with STOP 2 (Step 18) or with STOP 3 (Step 17) or with STOP 4 (Step 16) depending on the factual values of the job processing times. Note that $B=1$; see Algorithm 3.

Case (j): Algorithm 3 is stopped at step 18 (STOP 2).

Consider Step 2 and Step 3 of Algorithm 3. The schedule execution begins as follows: at the initial time-point $t=0$, machine $M_1$ starts to process operation $O_{1,1}$, while machine $M_2$ starts to process operation $O_{6,2}$. This process is continued until the time-point $t=4$ when machine $M_2$ completes operation $O_{6,2}$. At this time-point, an exact value of the processing time $p_{6,2}^{*}$ becomes known, namely: $p_{6,2}^{*}=4.$ Then, machine $M_2$ starts to process operation $O_{7,2}$ and machine $M_1$ continues the processing of operation $O_{1,1}$. At the time-point $t=6$, machine $M_1$ completes operation $O_{1,1}$. Therefore, an exact value of the duration of operation $O_{1,1}$ becomes known as follows: $p_{1,1}^{*}=6$. At this time-point, a scheduler needs to choose either job $J_2$ or job $J_3$ to be processed next on machine $M_1$. Note that machine $M_2$ continues to process the operation $O_{7,2}$ for two time units, wherein $l_{7,2}=3$.

Consider Step 4 of Algorithm 3, where the condition (12) of Theorem 9 is checked for the conflict set of jobs $\{J_2,J_3\}$. Due to equalities $k=1,$ $r=2,$ $c_1\left(1\right)=6,$ $c_2\left(6\right)=4$, one can obtain the following relations: $c_1\left(1\right)+u_{2,1}+u_{3,1}=6+9+9=23\nleqq c_2\left(6\right)+l_{7,2}+l_{8,2}+l_{5,2}+l_{1,2}=4+3+4+2+6=19.$

At Steps 6 and 7 of Algorithm 3, one can obtain $d_2=-4$, $d_3=-5$ and permutation ${\pi }_q$ having the following form: ${\pi }_q=(J_2,J_3).$ At Steps 8 and 9 of Algorithm 3, the conditions of Theorem 10 are checked as follows: $c_1\left(1\right)+u_{2,1}=6+9=15\le c_2\left(6\right)+l_{7,2}+l_{8,2}+l_{5,2}+l_{1,2}=4+3+4+2+6=19;$

$$c_1\left(1\right)+u_{2,1}+u_{3,1}=6+9+9=24\le c_2\left(6\right)+l_{7,2}+l_{8,2}+l_{5,2}+l_{1,2}+l_{2,2}=4+3+4+2+6+5=24.$$

At Step 11 of Algorithm 3, one can obtain the following strict order $A_{\prec }^{1,2}=(J_1\prec J_2\prec J_3)$ along with the permutation ${\pi }_{1,2}=(J_1,J_2,J_3)$. Since $b=1=B$ (see Step 13), Algorithm 3 is stopped at Step 18; see STOP 2. The optimal order of the conflict jobs $J_2$ and $J_3$ is found at the time-point $t=6$ and the pair of job permutations ${\pi }^{\prime }=(J_1,J_2,J_3,J_4,J_6,J_7,J_8)$ and ${\pi }^{″}=(J_6,J_7,J_8,J_5,J_1,J_2,J_3)$ is optimal for any scenario from the remaining set of possible scenarios $T(1,6)=\{p \in T:p_{1,1}^{*}=6,p_{6,2}^{*}=4\}.$

Thus, an additional information on the exact values of the processing times $p_{6,2}^{*}$ and $p_{1,1}^{*}$ allows a scheduler to find an optimal order of all conflict jobs. It schould be noted that the optimality of the constructed schedule is proven at the time-point $t=6$, i.e., before the end of the schedule execution.

At the time-point $t=6$, machine $M_1$ begins to process operation $O_{2,1}.$ Note that all the above checks are performed at the time-point $t=6.$

Case (jj): Algorithm 3 is stopped at Step 17 (STOP 3).

It is considered another possible realization of the semi-active schedule since another factual processing times are randomly generated at the on-line phase of scheduling for Example 2.

At the time-point $t=0$, machine $M_1$ begins to process operation $O_{1,1}$, while machine $M_2$ begins to process operation $O_{6,2}$. Let machine $M_2$ complete operation $O_{6,2}$ at the time-point $t=2.8$. Thus, the exact processing time $p_{6,2}^{*}=2.8$ becomes known. Then, machine $M_2$ begins to process operation $O_{7,2}$ and completes this process at the time-point $t=6$ (i.e., $p_{7,2}^{*}=3.2$), while machine $M_1$ continues processing operation $O_{1,1}$. Let at the time-point $t=6.9$, machine $M_1$ completes operation $O_{1,1}$ (i.e., $p_{1,1}^{*}=6.9$). One needs to choose either job $J_2$ or job $J_3$ to be processed next on machine $M_1$. At this time, machine $M_2$ continues to process the operation $O_{8,2}$ since $t=6$ and $(6.9-6)=0.9<4=l_{8,2}$.

Based on the checking of the condition (12) of Theorem 9 for the conflict set of the jobs, one can obtain the following relations: $k=1,$ $r=2,$ $c_1\left(1\right)=6.9,$ $c_2\left(7\right)=6;$

$$c_1\left(1\right)+u_{2,1}+u_{3,1}=6.9+9+9=23.9\nleqq c_2\left(7\right)+l_{8,2}+l_{5,2}+l_{1,2}=6+4+2+6=18.$$

Similarly as in the previous case (j), one can obtain $d_2=-4$, $d_3=-5$, and the permutation ${\pi }_q$ having the following form: ${\pi }_q=(J_2,J_3).$ The conditions of Theorem 10 are checked as follows:

$$c_1\left(1\right)+u_{2,1}=6.9+9=15.9\le c_2\left(7\right)+l_{8,2}+l_{5,2}+l_{1,2}=6+4+2+6=18;$$

$$c_1\left(1\right)+u_{2,1}+u_{3,1}=6.9+9+9=24.9\nleqq c_2\left(7\right)+l_{8,2}+l_{5,2}+l_{1,2}+l_{2,2}=6+4+2+6+5=23.$$

Thus, the conditions of Theorem 10 do not hold. At Step 10 of Algorithm 3, one can construct a Johnson’s permutation ${\pi }_q$ of the conflict jobs based on the inequalities (2) for the processing times of all conflict jobs determined as follows: $p_{ij}=(u_{ij}+l_{ij})/2$. For the jobs $J_2$ and $J_3$, one can calculate $p_{2,1}=8.5,$ $p_{2,2}=5.5,$ $p_{3,1}=8,$ $p_{3,2}=5$ and the Johnson’s permutation ${\pi }_q$ of the conflict jobs in the following form: ${\pi }_q=(J_2,J_3).$

At the time-point $t=6.9$, one can obtain the pair of permutations ${\pi }^{\prime }=(J_1,J_2,J_3,J_4,J_6,J_7,J_8)$ and ${\pi }^{″}=(J_6,J_7,J_8,J_5,J_1,J_2,J_3)$ of the jobs for their processing on machines $\mathcal{M}$. Therefore, at the time-point $t=6$, machine $M_1$ begins to process operation $O_{2,1}.$ Then, at the time-point $t=10$, machine $M_2$ completes operation $O_{8,2}$ (the exact processing time $p_{8,2}^{*}=4$ becomes known), and then begins to process operation $O_{5,2}$ till the time-point $t=12.4$ (thus, $p_{5,2}^{*}=2.4$), and then begins to process operation $O_{1,2}$. At the time-point $t=15.5$, machine $M_1$ completes operation $O_{2,1}$ (i.e., the exact processing time $p_{2,1}^{*}=8.6$ becomes known), and then begins to process operation $O_{3,1}.$

Then, at the time-point $t=18.7$, machine $M_2$ completes operation $O_{1,2}$ (the exact processing time $p_{1,2}^{*}=6.3$ becomes known), and then begins to process operation $O_{2,2}$ till the time-point $t=23.7$ (thus, $p_{2,2}^{*}=5$). At this time-point, machine $M_1$ still processes operation $O_{3,1}$. As a result, machine $M_2$ has an idle time in the realized schedule.

At the time-point $t=24.5$, machine $M_1$ completes operation $O_{3,1}$ (i.e., $p_{3,1}^{*}=9$), and then begins to process operation $O_{4,1}.$ Machine $M_2$ begins to process operation $O_{3,2}$ immediately.

At the time-point $t=26.5$, machine $M_1$ completes operation $O_{4,1}$ (i.e., $p_{4,1}^{*}=2$), and then begins to process operation $O_{6,1}$ till the time-point $t=27.5$ (i.e., $p_{6,1}^{*}=1$). Then, machine $M_1$ processes operation $O_{7,1}$ till the time-point $t=28.5$ (i,e., $p_{7,1}^{*}=1$), and then begins to process operation $O_{8,1}$.

At the time-point $t=30.5$, machine $M_2$ completes operation $O_{3,2}$ (i.e., the exact processing time $p_{3,2}^{*}=6$ becomes known). Thus, machine $M_2$ completes to process all jobs in the realized permutation ${\pi }^{″}$ at the time-point $c_2\left(3\right)=30.5.$ At the time-point $t=31.5$, machine $M_1$ completes operation $O_{8,1}$ (and the exact processing time $p_{8,1}^{*}=3$ becomes known). Thus, machine $M_1$ completes to process all jobs in the realized permutation ${\pi }^{\prime }$ at the time-point $c_1\left(8\right)=31.5.$

All uncertain processing times $p \in T$ took their factual values $p_{ij}^{*}$ as follows:

$$p^{*}=(p_{1,1}^{*},p_{1,2}^{*},p_{2,1}^{*},\dots ,p_{7,2}^{*},p_{8,1}^{*},p_{8,2}^{*})=(6.9,6.3,8.6,5,9,6,2,0,0,2.4,1,2.8,1,3.2,3,4).$$

It should be remind that these factual processing times $p^{*}$ were randomly generated at the time-points of the completions of the corresponding operations; see Remark 3.

For the constructed and realized schedule $({\pi }^{\prime },{\pi }^{″})$, the equalities $C_{max}({\pi }^{\prime },{\pi }^{″})=max\{c_1\left(8\right),c_2\left(3\right)\}=max\{31.5,30.5\}=31.5$ hold; see Step 14 of Algorithm 3.

Now, one can check whether the constructed and realized schedule $({\pi }^{\prime },{\pi }^{″})$ is optimal for the factual vector $p^{*}$ of the job processing times. To this end, one can construct the pair of Jackson’s permutations $({\pi }_{*}^{\prime },{\pi }_{*}^{″})$ for the deterministic problem $J2|p^{*},n_i\le 2|C_{max}$ with the factual vector $p^{*}$ of the job processing times. Then, one can find the optimal makespan value for the deterministic problem $J2|p^{*},n_i\le 2|C_{max}$ as follows: $C_{max}({\pi }_{*}^{\prime },{\pi }_{*}^{″})=31.5$; see Step 15 of Algorithm 3.

The obtained equalities $C_{max}({\pi }_{*}^{\prime },{\pi }_{*}^{″})=31.5=C_{max}({\pi }^{\prime },{\pi }^{″})$ mean that Algorithm 3 has constructed the optimal schedule for the deterministic problem $J2|p^{*},n_i\le 2|C_{max}$ with the factual vector $p^{*}$ of the job processing times. However, the optimality of this constructed and realized schedule $({\pi }^{\prime },{\pi }^{″})$ was established after the execution of the whole schedule $({\pi }^{\prime },{\pi }^{″})$. Indeed, Algorithm 3 is stopped at Step 17; see STOP 3. The constructed and realized schedule $({\pi }^{\prime },{\pi }^{\prime \prime })$ is presented in Figure 4 for case (jj) of the randomly generated factual processing times $p^{*}$ of the jobs $\mathcal{J}$.

Case (jjj): Algorithm 3 is stopped at Step 16 (STOP 4).

It is considered the same process as in the previous case (jj) up to the time-point $t=28.5$ when machine $M_1$ begins to process operation $O_{8,1}$ (machine $M_2$ processes operation $O_{3,2}$ at this time-point).

Let the equality $p_{8,1}^{**}=1$ hold for the factual processing time $p_{8,1}^{**}$ of the operation $O_{8,1}$ and machine $M_1$ complete operation $O_{8,1}$. Thus, machine $M_1$ completes all operations of the jobs $\mathcal{J}$ in the permutation ${\pi }^{\prime }$ at the time-point $29.5$. Therefore, the equality $c_1\left(8\right)=29.5$ holds. Similarly as in the previous case, machine $M_2$ completes operation $O_{3,2}$ at the time-point $t=30.5$. Thus, $p_{3,2}^{*}=6$ and $c_2\left(3\right)=30.5.$ The factual vector of the job processing times is randomly generated as follows:

$$p^{**}=(p_{1,1}^{*},p_{1,2}^{*},p_{2,1}^{*},\dots ,p_{7,2}^{*},p_{8,1}^{**},p_{8,2}^{*})=(6.9,6.3,8.6,5,9,6,2,0,0,2.4,1,2.8,1,3.2,1,4).$$

The makespan value for the constructed and realized schedule $({\pi }^{\prime },{\pi }^{″})$ is determined as follows: $C_{max}({\pi }^{\prime },{\pi }^{″})=max\{c_1\left(8\right),c_2\left(3\right)\}=max\{29.5,30.5\}=30.5.$ However, the optimal makespan value for the deterministic problem $J2|p^{**},n_i\le 2|C_{max}$ with the factual vector $p^{**}$ of the job processing times is equal to $29.7<30.5=C_{max}({\pi }^{\prime },{\pi }^{″})$, since the optimal order of the jobs $J_2$ and $J_3$ is determined as follows: $(J_3,J_2).$ Hence, the constructed and realized schedule $({\pi }^{\prime },{\pi }^{″})$ is not optimal for the factual vector $p^{**} \in T$ of the job processing times. In this case, Algorithm 3 is stopped at Step 16; see STOP 4.

6.3. Computational Experiments

We describe the computational experiments and computational results obtained for the tested randomly generated instances of the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. Each tested series consisted of 1000 randomly generated instances with fixed numbers $n \in \{10,20,\dots ,100\}$ of the jobs $\mathcal{J}$ and the maximum possible errors $\delta \in \{5\%,10\%,20\%,30\%,40\%,50\%,60\%,70\%,80\%,90\%,100\%\}$ of the random durations of the operations $O_{ij}$. The lower bounds $l_{ij}$ and upper bounds $u_{ij}$ on the possible values of the durations $p_{ij}$ of operations $O_{ij}$, $p_{ij} \in [l_{ij},u_{ij}],$ were randomly generated as follows. The lower bound $l_{ij}$ was randomly chosen from the segment $[10,100000]$ using a uniform distribution. The upper bound $u_{ij}$ was determined using the equality $u_{ij}=l_{ij}(1+\frac{\delta }{100})$. The bounds $l_{ij}$ and $u_{ij}$ are decimal fractions with the maximum numbers of digits after the decimal points. The inequality $l_{ij}<u_{ij}$ holds for each job $J_i \in \mathcal{J}$ and each machine $M_j \in \mathcal{M}$.

Algorithms 1 and 2 developed in [8] were used at the off-line phase of scheduling. If the tested instance was not optimally solved using Algorithms 1 and 2, then corresponding Algorithms 3, 4 or 5 was used at the on-line phase of scheduling for solving further the instance of the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. All developed algorithms were coded in C# and tested on a PC with Intel Core i7-7700 (TM) 4 Quad, 3.6 GHz, 32.00 GB RAM.

In the computational experiments, two procedures were used to generate factual durations of the operations $O_{ij}$ (a factual duration of the job $J_i$ remained unknown until completing this job). In the first part of the computational experiments, the factual duration $p_{ij}^{*}$ of the operation $O_{ij}$ was randomly generated using a uniform distribution in the range $[l_{ij},u_{ij}]$. In the second part of the computational experiments, two distribution laws were used in the experiments to determine the factual scenarios. Namely, we used the gamma distribution with parameters $(0.5;1)$ (we call it as the distribution law with number 1) and the gamma distribution with parameters $(7.5;1)$ (we call it as the distribution law with number 2). For generating factual processing times for each tested instance, the number of the used distribution was randomly chosen from the possible set $\{1,2\}$.

The sufficient conditions proven in Section 5 are verified in polynomial time $O\left(n^2\right)$ of the number n of the jobs $\mathcal{J}$. Therefore, all series of the tested instances in our computational experiments were solved very quickly (less than one second per a series with 1000 instances).

The experiments include testing of 14 classes of the instances of the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ with different ratios of the numbers $m_1$, $m_2$, $m_{1,2}$ and $m_{2,1}$ (where $n=m_1+m_2+m_{1,2}+m_{2,1}$) of the jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the set $\mathcal{J}$, respectively. Every class of the tested instances of the problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ is characterized by the following ratio:

$$\frac{m_1}{n}·100\%:\frac{m_2}{n}·100\%:\frac{m_{1,2}}{n}·100\%:\frac{m_{2,1}}{n}·100\%$$

(28)

of the percentages of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the set $\mathcal{J}$, respectively.

Table A1. Computational results for the randomly generated instances with the ratio 0%:0%:10%:90% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	93.9	97.3	98.4	97.6	96.6	97.6	97.9	98.3	98	97.5	93.4	97	97.7	97.1	98.5	98.3	97.6	98.6	98.3	98.7
	Stop2	0.9	1	0.6	1.1	1.6	1.3	1.2	1.1	0.9	1.4	0.8	0.8	0.9	1.1	0.5	0.5	1.3	0.8	0.9	0.6
	Stop3	5.1	1.7	1	1.3	1.8	1.1	0.9	0.6	1.1	1.1	5.3	2.2	1.4	1.8	1	1.2	1.1	0.6	0.8	0.7
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0.5	0	0	0	0	0	0	0	0	0
10	Stop1	85.8	91.8	91.6	93	92.2	92.2	91.9	92.6	93.6	93.8	83.1	93.5	92.8	92.7	93.1	92.3	92.4	93.3	94.2	93.6
	Stop2	2.1	2.5	4.5	3.5	4.1	4	4.2	4.6	4.2	4.2	3.2	2.8	3.1	3.5	3.6	4.3	4.2	3.4	3.5	4.1
	Stop3	11.7	5.7	3.9	3.5	3.7	3.8	3.9	2.8	2.2	2	12.8	3.7	4.1	3.8	3.3	3.4	3.4	3.3	2.3	2.3
	Stop4	0.4	0	0	0	0	0	0	0	0	0	0.9	0	0	0	0	0	0	0	0	0
20	Stop1	70.6	73.2	73.3	71.9	69.6	63.4	63.6	57.7	56.3	53.4	70.2	73.7	74.1	71.5	67.2	64.2	63.4	61.5	56.1	57.5
	Stop2	4.3	6.8	9.4	8.6	8.8	11.1	9.4	10.1	9.2	9.2	4.3	8.1	8.7	10	10	11.3	9.1	9.1	8.9	7.5
	Stop3	24.2	20	17.3	19.5	21.6	25.5	27	32.2	34.5	37.4	24.9	18.2	17.2	18.5	22.8	24.5	27.5	29.4	35	35
	Stop4	0.9	0	0	0	0	0	0	0	0	0	0.6	0	0	0	0	0	0	0	0	0
30	Stop1	53	55.1	47.5	41.1	31	30.7	23.4	20.3	18.5	13.4	52	52.2	44.9	34.9	33.6	26.3	27.3	18.3	18.9	14.2
	Stop2	4.8	8.8	9.1	9.7	9.8	7	6.7	5.2	4.2	4.4	6.2	8.9	10.1	10.4	11	7.9	6	4.6	5.9	4.5
	Stop3	41.9	36.1	43.4	49.2	59.2	62.3	69.9	74.5	77.3	82.2	41	38.9	45	54.7	55.4	65.8	66.7	77.1	75.2	81.3
	Stop4	0.3	0	0	0	0	0	0	0	0	0	0.8	0	0	0	0	0	0	0	0	0
40	Stop1	41.6	32.5	24.7	16.4	10.9	8.9	5.9	3.9	2.1	2.3	37.8	31.8	22.2	18.6	10.6	8.5	6.1	4.3	3	1.9
	Stop2	4.9	7.6	7.7	6.6	4.2	2.9	2	1.1	0.7	0.3	5.2	8.5	9.1	4.8	2.9	3.5	2	1.6	1	0.6
	Stop3	52.7	59.7	67.6	77	84.9	88.2	92.1	95	97.2	97.4	55.3	59.7	68.7	76.6	86.5	88	91.9	94.1	96	97.5
	Stop4	0.8	0.2	0	0	0	0	0	0	0	0	1.7	0	0	0	0	0	0	0	0	0
50	Stop1	29	16.1	9.3	5	2.4	1.4	1.6	0.8	0.5	0	26.2	19.4	10.4	5.6	3.9	1.6	0.6	0.5	0.3	0.1
	Stop2	4.7	5.4	5	2.6	1.2	0.8	0.2	0.3	0.3	0	3.7	5.6	3.8	2.2	0.7	0.7	0.7	0.1	0.2	0.1
	Stop3	64.9	78.5	85.7	92.4	96.4	97.8	98.2	98.9	99.2	100	67.8	75	85.8	92.2	95.4	97.7	98.7	99.4	99.5	99.8
	Stop4	1.4	0	0	0	0	0	0	0	0	0	2.3	0	0	0	0	0	0	0	0	0
60	Stop1	18.1	8.4	4.6	1.4	1	0.3	0.2	0.1	0	0	16.6	9.6	3.6	1.4	1	0.3	0	0.2	0	0
	Stop2	3.8	4	1.6	0.7	0.3	0.1	0	0	0	0	3.2	3.5	2.3	0.9	0.4	0	0.3	0	0.1	0
	Stop3	76.4	87.5	93.8	97.9	98.7	99.6	99.8	99.9	100	100	77.7	86.9	94.1	97.7	98.6	99.7	99.7	99.8	99.9	100
	Stop4	1.7	0.1	0	0	0	0	0	0	0	0	2.5	0	0	0	0	0	0	0	0	0
70	Stop1	12.3	5.1	1.4	0.7	0.1	0	0	0	0	0	12.1	4.7	2.1	0.8	0.2	0	0.1	0	0	0
	Stop2	2.8	1.5	0.7	0.2	0.1	0	0	0	0	0	2	2.1	0.4	0.2	0	0	0	0	0	0
	Stop3	83.2	93.4	97.9	99.1	99.8	100	100	100	100	100	82.8	93.2	97.5	99	99.8	100	99.9	100	100	100
	Stop4	1.7	0	0	0	0	0	0	0	0	0	3.1	0	0	0	0	0	0	0	0	0
80	Stop1	8.9	1.9	0.4	0.3	0.2	0	0	0	0	0	10	2.3	0.6	0.2	0	0	0	0	0	0
	Stop2	1.8	0.8	0.5	0	0	0	0	0	0	0	2.2	1.1	0.2	0	0	0.1	0	0	0	0
	Stop3	87.1	97.1	99.1	99.7	99.8	100	100	100	100	100	84.2	96.5	99.2	99.8	100	99.9	100	100	100	100
	Stop4	2.2	0.2	0	0	0	0	0	0	0	0	3.6	0.1	0	0	0	0	0	0	0	0
90	Stop1	6.9	0.8	0.2	0.1	0	0	0	0	0	0	5.7	0.9	0.3	0	0	0	0	0	0	0
	Stop2	1.2	0.7	0.1	0	0	0	0	0	0	0	1.5	0.5	0	0	0	0	0	0	0	0
	Stop3	90.1	98.4	99.7	99.9	100	100	100	100	100	100	88	98.5	99.7	100	100	100	100	100	100	100
	Stop4	1.8	0.1	0	0	0	0	0	0	0	0	4.8	0.1	0	0	0	0	0	0	0	0
100	Stop1	4.4	0.3	0.1	0.1	0	0	0	0	0	0	4.1	0.3	0	0	0	0	0	0	0	0
	Stop2	1.1	0.2	0	0	0	0	0	0	0	0	0.8	0	0	0	0	0	0	0	0	0
	Stop3	92.1	99.4	99.9	99.9	100	100	100	100	100	100	90.2	99.4	100	100	100	100	100	100	100	100
	Stop4	2.4	0.1	0	0	0	0	0	0	0	0	4.9	0.3	0	0	0	0	0	0	0	0

,

Table A2. Computational results for randomly generated instances with the ratio 0%:0%:20%:80% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	96.7	98.9	98.6	99.5	99.7	99.7	99.9	99.9	99.9	99.9	96.7	98.9	99	99.3	99.6	99.4	99.7	99.8	99.9	99.8
	Stop2	0.8	0.3	0.7	0.1	0	0.2	0.1	0.1	0.1	0.1	0.3	0.4	0.1	0.3	0.1	0.4	0.2	0.1	0.1	0.2
	Stop3	2.4	0.8	0.7	0.4	0.3	0.1	0	0	0	0	3	0.7	0.9	0.4	0.3	0.2	0.1	0.1	0	0
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	93.4	96.2	97.6	97.7	98	98.4	98.4	98.7	98.5	99.6	93.5	96.1	97.5	97.6	97.8	98.1	98.4	98.2	99	98.7
	Stop2	1	1.4	1.4	1.4	1.4	1.3	1.1	1.2	1	0.4	1	1.8	1.1	1.3	1.5	1.6	1.3	1.5	0.9	1.1
	Stop3	5.4	2.4	1	0.9	0.6	0.3	0.5	0.1	0.5	0	5.5	2.1	1.4	1.1	0.7	0.3	0.3	0.3	0.1	0.2
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	85.4	86.9	89.5	90.2	90.8	90.5	89.1	90	90.3	90.1	83.5	87.5	88.8	88.4	90.6	89.9	91	89.4	90.9	90.1
	Stop2	2.6	4.8	5.3	5	5.8	5.8	5.7	5	5	5.4	3.1	5.7	5.8	7.4	4.7	5.8	4.9	6.5	6.2	4
	Stop3	12	8.3	5.2	4.8	3.4	3.7	5.2	5	4.7	4.5	13.4	6.8	5.4	4.2	4.7	4.3	4.1	4.1	2.9	5.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	70.2	76.4	70.1	69.6	69.2	65.7	64.1	60.4	58	56	71.6	73.3	72.9	69	66	63.1	60.4	62.3	62.2	58.1
	Stop2	5.1	6.8	9.7	9.5	8.4	10.5	9.7	9.1	10.8	8.1	3.6	8.7	8.4	9.6	9.8	11.3	8.4	8.3	7.1	8.9
	Stop3	24.6	16.8	20.2	20.9	22.4	23.8	26.2	30.5	31.2	35.9	24.8	18	18.7	21.4	24.2	25.6	31.2	29.4	30.7	33
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	56.7	55.3	48.8	41.5	39.6	31.2	31.1	26.5	23.5	21.5	55.1	53.9	46.5	41.5	37.5	31.6	33.2	27.4	26.2	21
	Stop2	5.1	8.2	10.5	10.6	9.6	8.2	7.6	6.9	7.5	5	5.6	9.2	11.5	7.7	8.9	8.7	7.3	7.2	6	5.7
	Stop3	38.2	36.5	40.7	47.9	50.8	60.6	61.3	66.6	69	73.5	39.3	36.9	42	50.8	53.6	59.7	59.5	65.4	67.8	73.3
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
50	Stop1	42.6	35.2	27.2	22.9	14.3	11.4	9.9	6.9	6.6	5.9	43.9	37.3	29.2	22	16.3	13.2	10.8	10.5	5.5	5.7
	Stop2	4.4	9.5	9.8	6.5	6	5.2	3.8	3.4	2.2	2.4	6	10	7.3	6.9	6.5	4.8	4.7	2.8	1.9	2.5
	Stop3	52.8	55.3	63	70.6	79.7	83.4	86.3	89.7	91.2	91.7	49.9	52.7	63.5	71.1	77.2	82	84.5	86.7	92.6	91.8
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.2	0	0	0	0	0	0	0	0	0
60	Stop1	32.9	20.7	14.4	10.7	6.3	3.3	3.3	2.2	1.4	0.8	31.7	23.1	15.7	10.4	7.2	3.9	2.9	1.4	0.9	0.6
	Stop2	5.4	5.5	4.2	2.6	2.3	1.7	0.8	0.6	0.3	0.4	5.6	6	6.4	3.6	2.4	1.5	1.5	0.8	0.3	0.7
	Stop3	61.7	73.8	81.4	86.7	91.4	95	95.9	97.2	98.3	98.8	62.3	70.9	77.9	86	90.4	94.6	95.6	97.8	98.8	98.7
	Stop4	0	0	0	0	0	0	0	0	0	0	0.4	0	0	0	0	0	0	0	0	0
70	Stop1	22.1	13.7	7.6	2.9	1.6	1.1	0.6	0.2	0.3	0.1	23.9	13.1	6.7	3.4	1.6	0.7	0.9	0.3	0.2	0.1
	Stop2	4.9	3.7	2.9	1.7	0.9	0.6	0.4	0.1	0	0.1	4.4	4.5	2	1.5	1.2	0.4	0	0.4	0.1	0.1
	Stop3	72.8	82.6	89.5	95.4	97.5	98.3	99	99.7	99.7	99.8	71.6	82.4	91.3	95.1	97.2	98.9	99.1	99.3	99.7	99.8
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
80	Stop1	17.3	8.3	3.5	1.3	0.5	0.3	0.2	0	0	0	16.4	7.9	3.1	1.9	0.9	0.2	0	0	0	0
	Stop2	2.8	1.7	1.8	0.8	0.6	0	0	0	0	0	3.4	2.4	0.8	0.9	0.1	0.2	0.1	0	0	0
	Stop3	79.4	90	94.7	97.9	98.9	99.7	99.8	100	100	100	79.6	89.7	96.1	97.2	99	99.6	99.9	100	100	100
	Stop4	0.5	0	0	0	0	0	0	0	0	0	0.6	0	0	0	0	0	0	0	0	0
90	Stop1	12.1	4.5	1.4	0.7	0	0.1	0	0	0	0	12.6	5	2.9	0.4	0.1	0.1	0	0	0	0
	Stop2	2.5	2.3	1.3	0.3	0	0.1	0	0	0	0	3.2	1.8	0.2	0.2	0	0	0	0	0	0
	Stop3	85.2	93.2	97.3	99	100	99.8	100	100	100	100	83.7	93.2	96.9	99.4	99.9	99.9	100	100	100	100
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.5	0	0	0	0	0	0	0	0	0
100	Stop1	10.6	2.7	0.5	0.3	0	0	0	0	0	0	9.1	2.8	0.5	0.1	0	0	0	0	0	0
	Stop2	1.9	1.2	0.3	0	0.2	0	0	0	0	0	2	0.6	0.2	0	0	0	0	0	0	0
	Stop3	87.4	96.1	99.2	99.7	99.8	100	100	100	100	100	88.2	96.6	99.3	99.9	100	100	100	100	100	100
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0.7	0	0	0	0	0	0	0	0	0

,

Table A3. Computational results for randomly generated instances with the ratio 0%:0%:30%:70% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	99.2	99.6	99.9	99.9	100	100	100	100	100	100	98.6	99.9	99.9	99.9	99.9	100	100	100	100	100
	Stop2	0.2	0.1	0.1	0.1	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0
	Stop3	0.6	0.3	0	0	0	0	0	0	0	0	1.4	0.1	0.1	0.1	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	97.3	99	99.4	99.9	99.9	100	99.9	99.9	100	100	97.4	98.6	99.1	99.9	99.9	100	99.9	100	99.8	100
	Stop2	0.8	0.4	0.3	0.1	0.1	0	0.1	0.1	0	0	0.5	0.8	0.6	0.1	0.1	0	0.1	0	0.2	0
	Stop3	1.9	0.6	0.3	0	0	0	0	0	0	0	2.1	0.6	0.3	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	91.7	95.7	97.1	97.5	98.2	98.6	98.7	98.7	99.7	98.9	91.5	97	97.8	97.2	98.5	98.8	99.1	99.6	99.5	99.4
	Stop2	1.9	2.6	2	2.1	1.4	1.2	1.2	1.1	0.3	0.8	2.3	1.7	1.6	2.1	1.2	1	0.7	0.4	0.5	0.4
	Stop3	6.4	1.7	0.9	0.4	0.4	0.2	0.1	0.2	0	0.3	6.2	1.3	0.6	0.7	0.3	0.2	0.2	0	0	0.2
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	81.9	87.1	89.1	91.9	91.7	92.2	92.2	93.8	93.7	93.9	83	87.2	91.7	91.7	92.4	91.6	92.2	92.8	92.9	93.4
	Stop2	4.6	6.2	5.9	4.5	5.5	4.3	4.3	3.9	2.8	2.5	3.1	5.1	4.1	4.4	3.7	4.4	4.8	4.2	3.5	3.5
	Stop3	13.5	6.7	5	3.6	2.8	3.5	3.5	2.3	3.5	3.6	13.9	7.7	4.2	3.9	3.9	4	3	3	3.6	3.1
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	74.1	74.7	75.9	76	75.1	75.9	73.4	75.8	71.6	72.5	69.1	74.2	76.4	75.6	76.5	76.4	75	74	75.3	72.7
	Stop2	4.4	7.9	7.5	8.2	6.5	6.3	6.9	5.5	6.9	7	6	9.2	7.5	8	7.7	6.4	6.4	7.1	4.6	6.4
	Stop3	21.5	17.4	16.6	15.8	18.4	17.8	19.7	18.7	21.5	20.5	24.8	16.6	16.1	16.4	15.8	17.2	18.6	18.9	20.1	20.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
50	Stop1	61.4	60.7	56.9	53.7	50.4	49.7	47.3	47.3	44.7	39.1	58.2	60.6	57.7	51.7	49.1	50.9	48.3	48.2	43.9	44.3
	Stop2	5.3	9.2	9.7	10.4	10.2	7.7	8.4	7.1	6.7	6.3	5.8	8.7	8.5	12.4	10.2	9.1	7.8	7.1	6.6	5.3
	Stop3	33.3	30.1	33.4	35.9	39.4	42.6	44.3	45.6	48.6	54.6	36	30.7	33.8	35.9	40.7	40	43.9	44.7	49.5	50.4
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
60	Stop1	46.7	46.3	39.6	32.9	30.5	29.5	23.9	22.1	18.8	17.8	50.9	42.8	41.7	35.9	30.6	28	24	22.9	19	13.5
	Stop2	6.2	8.1	7.7	7.9	6.2	5.3	4.6	4.1	4.2	2.8	5	9.1	7.5	7.5	7.1	5.1	5.2	4.6	3.7	3.6
	Stop3	47.1	45.6	52.7	59.2	63.3	65.2	71.5	73.8	77	79.4	44.1	48.1	50.8	56.6	62.3	66.9	70.8	72.5	77.3	82.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
70	Stop1	39.9	34.5	24.5	20.2	17.6	12.2	8.7	8.6	7.6	5.5	38	34.8	23.5	19.1	15.7	13.7	9.5	9	6	4.7
	Stop2	5.7	7.4	6.7	5.5	4.1	2.8	2.7	1.9	1.4	0.9	6	6.8	6.3	5.6	3.9	4.8	3.4	1.4	1.4	1.3
	Stop3	54.4	58.1	68.8	74.3	78.3	85	88.6	89.5	91	93.6	55.9	58.4	70.2	75.3	80.4	81.5	87.1	89.6	92.6	94
	Stop4	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
80	Stop1	27.9	21.6	14.3	8.3	7.2	4.9	4.2	2.7	0.9	0.8	28.5	21.6	14	9.5	9.3	4.2	3.9	2.2	1.2	1.5
	Stop2	4.8	5	3.6	3	2.6	1.6	0.7	1	0.2	0.3	5.6	5.6	5.2	3.1	1.9	2.3	1.7	0.6	0.7	0.3
	Stop3	67.2	73.4	82.1	88.7	90.2	93.5	95.1	96.3	98.9	98.9	65.9	72.8	80.8	87.4	88.8	93.5	94.4	97.2	98.1	98.2
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
90	Stop1	22.7	13.2	9.8	4.1	2.1	1.5	1.4	0.7	0.2	0	23	14.4	7.4	3.6	3.4	1.9	1.2	0.7	0.3	0.9
	Stop2	3.4	4.7	3.1	1.9	1.4	0.9	0.5	0.3	0.3	0.2	3.4	5.1	2.9	2	1	0.6	0.7	0.2	0.2	0.3
	Stop3	73.9	82.1	87.1	94	96.5	97.6	98.1	99	99.5	99.8	73.4	80.5	89.7	94.4	95.6	97.5	98.1	99.1	99.5	98.8
	Stop4	0	0	0	0	0	0	0	0	0	0	0.2	0	0	0	0	0	0	0	0	0
100	Stop1	17.1	8.9	3.8	2.1	1.2	0.6	0.2	0.2	0	0	14.7	8	4.7	2.5	1.4	0.3	0.3	0.2	0.1	0.1
	Stop2	2.6	4.3	1.6	1.5	0.4	0.2	0.2	0	0	0	4.6	2.4	1.7	0.6	0.5	0.3	0.3	0.1	0.1	0
	Stop3	80.3	86.8	94.6	96.4	98.4	99.2	99.6	99.8	100	100	80.4	89.6	93.6	96.9	98.1	99.4	99.4	99.7	99.8	99.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0.3	0	0	0	0	0	0	0	0	0

,

Table A4. Computational results for randomly generated instances with the ratio 0%:0%:40%:60% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	99.8	100	100	100	100	100	100	100	100	100	99.5	99.8	99.9	100	99.9	100	100	100	100	100
	Stop2	0.1	0	0	0	0	0	0	0	0	0	0.1	0	0.1	0	0.1	0	0	0	0	0
	Stop3	0.1	0	0	0	0	0	0	0	0	0	0.4	0.2	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	99.2	99.7	99.9	100	100	100	100	100	100	100	98.9	100	99.9	100	100	100	100	100	100	100
	Stop2	0.4	0.3	0.1	0	0	0	0	0	0	0	0.2	0	0.1	0	0	0	0	0	0	0
	Stop3	0.4	0	0	0	0	0	0	0	0	0	0.9	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	96.8	98.9	99.4	99.5	99.9	99.8	100	100	100	99.9	96.4	98.6	99.6	99.7	99.9	100	100	100	100	100
	Stop2	1.1	0.6	0.4	0.5	0.1	0.2	0	0	0	0.1	1.6	0.8	0.4	0.3	0	0	0	0	0	0
	Stop3	2.1	0.5	0.2	0	0	0	0	0	0	0	2	0.6	0	0	0.1	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	91	95.7	97.8	98.7	99.2	99.5	99.4	99.8	99.9	100	91.8	94.9	97.3	98.6	99.1	99.6	99.9	99.9	99.7	100
	Stop2	3.5	1.7	1.2	0.9	0.7	0.2	0.4	0.1	0.1	0	2.3	3	1.8	1.1	0.7	0.3	0.1	0.1	0.3	0
	Stop3	5.5	2.6	1	0.4	0.1	0.3	0.2	0.1	0	0	5.9	2.1	0.9	0.3	0.2	0.1	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	85.8	90.4	93.7	95.1	96.4	97.6	97.2	98.2	98.3	98.5	85.4	91.2	93	94.8	96.5	97.4	97.3	98	98.2	98
	Stop2	2.7	4.5	3.5	1.6	1.9	1.3	2.1	0.6	1	1	3.7	3.7	3.2	2.9	1.8	1.6	0.8	1.2	0.7	1.1
	Stop3	11.5	5.1	2.8	3.3	1.7	1.1	0.7	1.2	0.7	0.5	10.9	5.1	3.8	2.3	1.7	1	1.9	0.8	1.1	0.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
50	Stop1	75.3	82.5	84.8	87.4	87	88.2	89.7	90.7	90.5	92.3	76.3	82.5	82.4	85.4	87.5	89.7	89.6	90.4	90.7	91.3
	Stop2	5.1	5.5	6	4.4	5.1	3.8	3.7	3.3	3	3	4.1	5.9	6	5.9	3.9	3.5	3.3	2.4	2.7	2.4
	Stop3	19.6	12	9.2	8.2	7.9	8	6.6	6	6.5	4.7	19.6	11.6	11.6	8.7	8.6	6.8	7.1	7.2	6.6	6.3
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
60	Stop1	63.4	70.1	72.3	74.7	75.8	73.9	72.5	75.4	75.4	76.6	66.3	71	73.7	75.2	72.9	73.2	73.7	71.9	75.5	75.2
	Stop2	6.6	7	7.8	6.6	5.8	4.3	6.6	4.2	3.9	4.5	4.7	7.4	7	5.9	5.8	5.4	4.2	5.2	5.3	3.1
	Stop3	30	22.9	19.9	18.7	18.4	21.8	20.9	20.4	20.7	18.9	29	21.6	19.3	18.9	21.3	21.4	22.1	22.9	19.2	21.7
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
70	Stop1	51.6	60	57.2	55.7	56.5	52.9	50.5	50.9	50.8	50	49.5	57	54.6	55.1	54.8	53.2	52.8	49.9	50	51.5
	Stop2	6.3	7.5	8.3	7.3	6.1	5.8	7.2	6.2	5.7	4.2	6.3	8.6	8	7.2	6.5	5.6	7	5.9	5.2	5.7
	Stop3	42.1	32.5	34.5	37	37.4	41.3	42.3	42.9	43.5	45.8	44.2	34.4	37.4	37.7	38.7	41.2	40.2	44.2	44.8	42.8
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
80	Stop1	39.8	43.9	39.4	39	37.8	34.8	31.7	31.1	30	28.1	39	43.7	40.1	40.3	41.1	31.3	31.5	28.1	26	28.2
	Stop2	6.3	7.3	8.5	7.4	6.1	4.9	3.7	4.4	4.2	3.3	5.9	8.1	7.8	5.9	6.6	5.7	4.7	3.6	4.6	3
	Stop3	53.9	48.8	52.1	53.6	56.1	60.3	64.6	64.5	65.8	68.6	55.1	48.2	52.1	53.8	52.3	63	63.8	68.3	69.4	68.8
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
90	Stop1	33.7	28.9	27.6	24.1	20.7	18.2	16.8	13.5	14.1	12.4	31.7	32.1	28.8	23.8	23.8	20.1	17.1	15.9	14.2	12.3
	Stop2	6	7.7	6.9	5.3	4.5	3.3	3.6	2.8	2.6	1.7	5.7	7.1	5.9	6	4.7	3.5	3.8	3	3.1	1.6
	Stop3	60.3	63.4	65.5	70.6	74.8	78.5	79.6	83.7	83.3	85.9	62.5	60.8	65.3	70.2	71.5	76.4	79.1	81.1	82.7	86.1
	Stop4	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
100	Stop1	26.1	21.4	15.6	13.1	11.1	7.9	7.3	6	4.4	4.6	24.1	21.2	16.7	16.2	11	8.2	8.3	6.7	5.7	3.8
	Stop2	3.9	6.4	5.4	4.6	3.2	2.9	1.8	1.6	0.7	1.3	5	6.2	5	2.9	3.4	3.4	2.5	1.5	1.9	1
	Stop3	70	72.2	79	82.3	85.7	89.2	90.9	92.4	94.9	94.1	70.9	72.6	78.3	80.9	85.6	88.4	89.2	91.8	92.4	95.2
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

,

Table A5. Computational results for randomly generated instances with the ratio 0%:0%:50%:50% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100
	Stop2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	99.8	100	100	100	100	100	100	100	100	100	99.9	100	100	100	100	100	100	100	100	100
	Stop2	0.1	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
	Stop3	0.1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	99.1	99.6	100	100	100	100	100	100	100	100	98.9	99.9	100	100	100	100	100	100	100	100
	Stop2	0.3	0.2	0	0	0	0	0	0	0	0	0.5	0.1	0	0	0	0	0	0	0	0
	Stop3	0.6	0.2	0	0	0	0	0	0	0	0	0.6	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	96.2	99.5	99.6	99.8	99.9	100	100	100	100	100	96.1	98.7	99.8	100	100	100	100	100	100	100
	Stop2	1.5	0.5	0.4	0.2	0.1	0	0	0	0	0	1.1	1.1	0.1	0	0	0	0	0	0	0
	Stop3	2.3	0	0	0	0	0	0	0	0	0	2.8	0.2	0.1	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	91.3	97.4	99.2	99.2	99.6	99.9	100	100	100	100	91.4	96.7	98.9	99.1	99.7	99.6	99.9	100	100	100
	Stop2	3	1	0.2	0.5	0.1	0.1	0	0	0	0	2.1	1.7	0.6	0.7	0.3	0.2	0.1	0	0	0
	Stop3	5.7	1.6	0.6	0.3	0.3	0	0	0	0	0	6.5	1.6	0.5	0.2	0	0.2	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
50	Stop1	83.4	92.3	95.3	97.9	98.2	98.8	99.3	99.9	99.8	100	81.7	90	95.5	97.5	98.7	98.9	99.4	99.8	99.9	99.9
	Stop2	3.5	3.3	1.9	1.1	0.9	0.6	0.1	0.1	0.1	0	3.8	4.6	2.1	1.3	0.5	0.5	0.4	0	0	0
	Stop3	13.1	4.4	2.8	1	0.9	0.6	0.6	0	0.1	0	14.5	5.4	2.4	1.2	0.8	0.6	0.2	0.2	0.1	0.1
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
60	Stop1	69.4	83.1	87.1	93.8	94.5	96.1	96.4	97.8	98.6	98.3	71.2	81.5	89.2	92.6	93.5	95.1	98	98.2	98.5	98.9
	Stop2	5.7	6.7	5	2.5	2.2	1.3	0.8	0.7	0.4	0.6	6.5	6.8	3.3	3.3	2.3	2.1	0.5	0.8	0.7	0.1
	Stop3	24.9	10.2	7.9	3.7	3.3	2.6	2.8	1.5	1	1.1	22.3	11.7	7.5	4.1	4.2	2.8	1.5	1	0.8	1
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
70	Stop1	59.2	70.2	75.5	81.1	81.6	88.1	87.9	92.4	92.8	93.6	58.4	72.7	74.8	81.5	85.8	87.8	88	91	90.3	93.7
	Stop2	5.8	7.4	6.6	6	5.2	4.1	3.7	1.7	1.1	2.4	4.3	8.3	7.6	4.4	3.6	3.2	4.1	2.4	2.6	2
	Stop3	35	22.4	17.9	12.9	13.2	7.8	8.4	5.9	6.1	4	37.3	19	17.6	14.1	10.6	9	7.9	6.6	7.1	4.3
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
80	Stop1	45	57.2	61.8	62.7	67.8	68.7	71	74.9	75.5	77	46.8	54.8	61.1	64.1	69.4	71	71.4	73.8	75.8	76
	Stop2	7	8.5	7.2	7.4	7.5	6	6	5.2	4.2	3.9	5.5	7.5	7	7.7	6.4	5.3	6.4	4.5	4.4	3.5
	Stop3	48	34.3	31	29.9	24.7	25.3	23	19.9	20.3	19.1	47.7	37.7	31.9	28.2	24.2	23.7	22.2	21.7	19.8	20.5
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
90	Stop1	35.2	41.2	38.7	44.2	42.5	45.6	46.2	45.2	50.3	50	37.2	37.3	41.3	43.8	43.3	46.5	48	46.7	47.5	49.4
	Stop2	6	8.3	9.8	7.7	7.8	7.4	6.4	6.2	6.4	5.5	5.4	8.7	9.8	8.9	9.3	9.2	6.4	6.9	6.2	5.7
	Stop3	58.8	50.5	51.5	48.1	49.7	47	47.4	48.6	43.3	44.5	57.4	54	48.9	47.3	47.4	44.3	45.6	46.4	46.3	44.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
100	Stop1	25.7	28.8	25.2	22.6	21.4	21.4	20.2	20.5	19	22.1	26.5	26	25.2	25.5	25.1	22.1	22.8	19.9	23.8	20.7
	Stop2	4.1	8.6	8.1	6.9	7.9	5.9	6.6	5.4	5.5	4.3	3.7	9.2	7.8	6	7.2	7.1	5.4	5.1	4.8	4.9
	Stop3	70.2	62.6	66.7	70.5	70.7	72.7	73.2	74.1	75.5	73.6	69.8	64.8	67	68.5	67.7	70.8	71.8	75	71.4	74.4
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

,

Table A6. Computational results for randomly generated instances with the ratio 5%:5%:5%:85% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions					Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	20	40	60	80	100	20	40	60	80	100
5	Stop1	99	99.5	99.7	99.3	99.4	98.1	99.7	99.8	99.2	99.7
	Stop2	0.3	0.3	0.2	0.4	0.6	0.4	0.2	0	0.6	0.3
	Stop3	0.7	0.2	0.1	0.3	0	1.5	0.1	0.2	0.2	0
	Stop4	0	0	0	0	0	0	0	0	0	0
10	Stop1	96.4	97.4	98.4	97.8	97.1	95.4	97.6	97.7	98	98.6
	Stop2	0.9	1.1	0.7	1.2	0.7	1.5	1.4	1	1.3	0.3
	Stop3	2.7	1.5	0.9	1	2.2	3.1	1	1.3	0.7	1.1
	Stop4	0	0	0	0	0	0	0	0	0	0
20	Stop1	84.3	81.4	76.5	71.7	67.9	86.5	80.5	73.8	71	66.5
	Stop2	3.1	3.5	3.7	2.5	2.1	2.9	3.5	2.9	3.7	1.7
	Stop3	12.6	15.1	19.8	25.8	30	10.6	16	23.3	25.3	31.8
	Stop4	0	0	0	0	0	0	0	0	0	0
30	Stop1	61.8	52.9	38.4	27.1	20.9	65.1	53	40	29.3	20.3
	Stop2	5.7	2.9	2.1	2.1	0.3	3.4	2.6	1.4	1.4	1.2
	Stop3	32.5	44.2	59.5	70.8	78.8	31.4	44.4	58.6	69.3	78.5
	Stop4	0	0	0	0	0	0.1	0	0	0	0
40	Stop1	38.6	25.5	14.1	7.3	3.1	40	24.4	13.6	6.5	3.2
	Stop2	5.4	1.2	1.2	0.4	0.3	4.5	2.4	0.4	0.4	0.1
	Stop3	56	73.3	84.7	92.3	96.6	55.5	73.2	86	93.1	96.7
	Stop4	0	0	0	0	0	0	0	0	0	0
50	Stop1	27.4	8.4	3.2	1.7	0.3	25.9	10.9	3.3	0.9	0.3
	Stop2	2.3	1.4	0.3	0	0	3.7	1.1	0	0	0
	Stop3	70.2	90.2	96.5	98.3	99.7	70.4	88	96.7	99.1	99.7
	Stop4	0.1	0	0	0	0	0	0	0	0	0
60	Stop1	14.3	3.4	0.5	0.2	0	15.7	3.2	0.6	0.3	0
	Stop2	2.3	0.4	0	0	0	1.8	0.1	0.3	0	0
	Stop3	83.4	96.2	99.5	99.8	100	82.4	96.7	99.1	99.7	100
	Stop4	0	0	0	0	0	0.1	0	0	0	0
70	Stop1	8	1.1	0.3	0	0	6.5	1.7	0.1	0	0
	Stop2	0.9	0	0	0	0	1.5	0	0.1	0	0
	Stop3	91.1	98.9	99.7	100	100	91.8	98.3	99.8	100	100
	Stop4	0	0	0	0	0	0.2	0	0	0	0
80	Stop1	4	0.1	0	0.1	0	5.1	0.2	0	0	0
	Stop2	0.5	0.1	0	0	0	0.9	0	0	0	0
	Stop3	95.5	99.8	100	99.9	100	93.8	99.8	100	100	100
	Stop4	0	0	0	0	0	0.2	0	0	0	0
90	Stop1	2.6	0.3	0	0	0	2.2	0	0	0	0
	Stop2	0.3	0	0	0	0	0.4	0	0	0	0
	Stop3	97.1	99.7	100	100	100	97	100	100	100	100
	Stop4	0	0	0	0	0	0.4	0	0	0	0
100	Stop1	0.9	0	0	0	0	1.5	0	0	0	0
	Stop2	0.3	0	0	0	0	0	0	0	0	0
	Stop3	98.8	100	100	100	100	98.4	100	100	100	100
	Stop4	0	0	0	0	0	0.1	0	0	0	0

,

Table A7. Computational results for randomly generated instances with the ratio 5%:15%:5%:75% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions					Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	20	40	60	80	100	20	40	60	80	100
5	Stop1	98.9	99.4	99.3	99.7	99.5	98.4	99.7	99.4	99.7	99.7
	Stop2	0.2	0.3	0.4	0.3	0.3	0.4	0.2	0.2	0.2	0.2
	Stop3	0.9	0.3	0.3	0	0.2	1.2	0.1	0.4	0.1	0.1
	Stop4	0	0	0	0	0	0	0	0	0	0
10	Stop1	97	98.2	97.7	98.6	99.3	95.5	98.6	98.6	98.4	98.3
	Stop2	1	0.8	1.1	0.7	0.3	1.3	0.8	0.8	0.7	0.9
	Stop3	2	1	1.2	0.7	0.4	3.2	0.6	0.6	0.9	0.8
	Stop4	0	0	0	0	0	0	0	0	0	0
20	Stop1	86	86.7	83.3	76.9	75.4	88.3	86.1	83.3	77.4	74.6
	Stop2	2.6	2.8	2.5	3.1	2.5	2.5	2.3	3.1	2.7	2.3
	Stop3	11.4	10.5	14.2	20	22.1	9.2	11.6	13.6	19.9	23.1
	Stop4	0	0	0	0	0	0	0	0	0	0
30	Stop1	67.1	58.1	47.1	36.1	29.3	69	64.5	48.2	38.6	28.7
	Stop2	3.1	3.2	2.8	2.6	1.5	3.2	2.1	2.2	2	1.2
	Stop3	29.8	38.7	50.1	61.3	69.2	27.8	33.4	49.6	59.4	70.1
	Stop4	0	0	0	0	0	0	0	0	0	0
40	Stop1	48.2	30.1	18.9	11.1	8.3	45.6	31.8	17.6	10.5	6.6
	Stop2	2.7	3.7	1.2	0.3	0.1	4.3	2.6	1.9	0.7	0.3
	Stop3	49.1	66.2	79.9	88.6	91.6	50.1	65.6	80.5	88.8	93.1
	Stop4	0	0	0	0	0	0	0	0	0	0
50	Stop1	30.1	15.1	7.4	3	1.2	29.1	13.2	6	2.7	1.7
	Stop2	2.8	1.3	0.7	0.3	0	2.6	1.1	0.3	0.2	0
	Stop3	67.1	83.6	91.9	96.7	98.8	68.3	85.7	93.7	97.1	98.3
	Stop4	0	0	0	0	0	0	0	0	0	0
60	Stop1	19.2	7.6	1.9	0.5	0	21.1	5.9	2.6	0.5	0.3
	Stop2	1.5	0.4	0	0	0.1	2	0.5	0.2	0	0
	Stop3	79.3	92	98.1	99.5	99.9	76.9	93.6	97.2	99.5	99.7
	Stop4	0	0	0	0	0	0	0	0	0	0
70	Stop1	11.4	2.6	0.9	0	0	12	3.1	0.3	0	0.1
	Stop2	1.9	0.1	0	0	0	0.8	0.2	0	0	0
	Stop3	86.7	97.3	99.1	100	100	87.2	96.7	99.7	100	99.9
	Stop4	0	0	0	0	0	0	0	0	0	0
80	Stop1	7.6	1.2	0.1	0	0	7.9	0.6	0.2	0	0
	Stop2	0.7	0.1	0	0	0	1	0.1	0	0	0
	Stop3	91.7	98.7	99.9	100	100	91.1	99.3	99.8	100	100
	Stop4	0	0	0	0	0	0	0	0	0	0
90	Stop1	3.4	0.6	0.1	0	0	4.6	0.5	0.1	0	0
	Stop2	0.4	0	0	0	0	0.5	0	0	0	0
	Stop3	96.2	99.4	99.9	100	100	94.9	99.5	99.9	100	100
	Stop4	0	0	0	0	0	0	0	0	0	0
100	Stop1	2.7	0.2	0	0	0	2.9	0.2	0	0	0
	Stop2	0.5	0	0	0	0	0.3	0	0	0	0
	Stop3	96.8	99.8	100	100	100	96.8	99.8	100	100	100
	Stop4	0	0	0	0	0	0	0	0	0	0

,

Table A8. Computational results for randomly generated instances with the ratio 5%:20%:5%:70% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions					Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	20	40	60	80	100	20	40	60	80	100
5	Stop1	98.6	99.2	99.6	99.4	99.5	98.3	99.2	99.7	99.8	99.6
	Stop2	0.1	0.4	0.3	0.4	0.5	0.5	0.1	0.1	0.1	0.3
	Stop3	1.3	0.4	0.1	0.2	0	1.2	0.7	0.2	0.1	0.1
	Stop4	0	0	0	0	0	0	0	0	0	0
10	Stop1	96.1	98.5	99.7	99.1	99.1	96.6	98.2	98.2	98.9	98.4
	Stop2	1.1	0.6	0.2	0.7	0.4	0.3	0.9	1.2	0.6	0.9
	Stop3	2.8	0.9	0.1	0.2	0.5	3.1	0.9	0.6	0.5	0.7
	Stop4	0	0	0	0	0	0	0	0	0	0
20	Stop1	88.8	87.6	84.6	80.1	77.6	89.5	89.8	84.6	83.5	79.3
	Stop2	1.9	2.4	2.6	2.2	2.8	3	1.9	2.7	1.9	2.4
	Stop3	9.3	10	12.8	17.7	19.6	7.5	8.3	12.7	14.6	18.3
	Stop4	0	0	0	0	0	0	0	0	0	0
30	Stop1	72	62.3	52.3	43.2	33.5	70.6	63.1	53	42.4	36.9
	Stop2	3.4	2.2	3.9	3	1.8	3.9	3.4	3.9	2.5	0.6
	Stop3	24.6	35.5	43.8	53.8	64.7	25.5	33.5	43.1	55.1	62.5
	Stop4	0	0	0	0	0	0	0	0	0	0
40	Stop1	50.6	37.1	25.9	15	9.9	50.7	36.4	25.9	16.5	10.3
	Stop2	3.7	2.1	1.8	0.7	0.4	3.5	2.7	1.3	1	0.4
	Stop3	45.7	60.8	72.3	84.3	89.7	45.8	60.9	72.8	82.5	89.3
	Stop4	0	0	0	0	0	0	0	0	0	0
50	Stop1	36.2	19.5	9.4	4.5	1.7	33.2	17.9	9.6	4.3	2.8
	Stop2	3.1	1.6	0	0.1	0.2	3.9	0.9	0.6	0.3	0
	Stop3	60.7	78.9	90.6	95.4	98.1	62.9	81.2	89.8	95.4	97.2
	Stop4	0	0	0	0	0	0	0	0	0	0
60	Stop1	25.2	7.7	3.1	1.2	0.3	24	7.6	3.5	0.6	0.5
	Stop2	2	0.7	0.3	0	0	1.6	1.2	0.2	0	0
	Stop3	72.8	91.6	96.6	98.8	99.7	74.4	91.2	96.3	99.4	99.5
	Stop4	0	0	0	0	0	0	0	0	0	0
70	Stop1	12	3.3	0.8	0.2	0.4	16.6	4.1	1.6	0.5	0.1
	Stop2	2.3	0.4	0.1	0	0	1.1	0.7	0	0	0
	Stop3	85.7	96.3	99.1	99.8	99.6	82.3	95.2	98.4	99.5	99.9
	Stop4	0	0	0	0	0	0	0	0	0	0
80	Stop1	9.4	1.8	0.3	0	0	9.9	1.8	0.1	0	0
	Stop2	1.4	0.1	0	0	0	1	0.1	0	0	0
	Stop3	89.2	98.1	99.7	100	100	89	98.1	99.9	100	100
	Stop4	0	0	0	0	0	0.1	0	0	0	0
90	Stop1	5.6	0.3	0.1	0.1	0	6.5	0.6	0.1	0	0
	Stop2	0.7	0.1	0	0	0	0.3	0.1	0	0	0
	Stop3	93.7	99.6	99.9	99.9	100	93.2	99.3	99.9	100	100
	Stop4	0	0	0	0	0	0	0	0	0	0
100	Stop1	4.5	0.5	0	0	0	4.5	0.2	0	0	0
	Stop2	0.2	0	0	0	0	0.2	0	0	0	0
	Stop3	95.3	99.5	100	100	100	95.3	99.8	100	100	100
	Stop4	0	0	0	0	0	0	0	0	0	0

,

Table A9. Computational results for randomly generated instances with the ratio 10%:10%:10%:70% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	98.9	99.5	100	99.8	100	99.9	100	100	100	99.9	98.4	99.4	99.9	100	99.9	99.9	100	100	100	100
	Stop2	0.4	0	0	0.2	0	0	0	0	0	0.1	0	0.3	0.1	0	0	0.1	0	0	0	0
	Stop3	0.7	0.5	0	0	0	0.1	0	0	0	0	1.6	0.3	0	0	0.1	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	95.9	98.9	98.9	100	99.8	100	100	100	99.9	99.9	96.2	98.4	99.5	99.7	99.8	99.9	99.9	99.8	99.8	99.9
	Stop2	0.2	0.5	0.6	0	0.2	0	0	0	0.1	0	0.3	0.3	0.2	0.1	0.1	0.1	0.1	0.2	0.2	0.1
	Stop3	3.8	0.6	0.5	0	0	0	0	0	0	0.1	3.4	1.3	0.3	0.2	0.1	0	0	0	0	0
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
20	Stop1	88.8	97	97.1	97.8	97.8	97.5	98.2	98.7	97.5	97.9	88.5	95.3	96.5	97.2	97.6	97.3	97.9	98.3	98.2	97.5
	Stop2	1.6	1.2	1.1	0.5	0.6	1	0.6	0.4	0.2	0.2	1.6	1.6	1	1.3	0.5	0.7	0.8	0.7	0.6	0.4
	Stop3	9.5	1.8	1.8	1.7	1.6	1.5	1.2	0.9	2.3	1.9	9.8	3.1	2.5	1.5	1.9	2	1.3	1	1.2	2.1
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
30	Stop1	79.3	85.8	86.6	85.1	81.4	83.3	82.6	79.2	77.4	75.9	80.4	86.3	86.5	85.1	81.2	81.6	80.8	80	79	76.1
	Stop2	3.7	2.2	2.5	1.7	2.9	1.8	1.5	1.2	1.5	1	2.4	2.8	2.8	1.7	1.9	1.4	1.4	1.3	1	0.6
	Stop3	17	12	10.9	13.2	15.7	14.9	15.9	19.6	21.1	23.1	16.9	10.9	10.7	13.2	16.9	17	17.8	18.7	20	23.3
	Stop4	0	0	0	0	0	0	0	0	0	0	0.3	0	0	0	0	0	0	0	0	0
40	Stop1	66.6	71.7	65.8	62.2	58.2	53.1	48.4	44	42	38.3	65.8	70.1	65.8	60.9	57.4	52.7	53.9	46.8	40.6	38.5
	Stop2	3	2.6	2.4	2.8	2.2	2.4	1.7	2	1.1	0.9	2.6	2.7	2.6	1.8	1.6	1.5	2.1	1	0.9	1.1
	Stop3	30.2	25.7	31.8	35	39.6	44.5	49.9	54	56.9	60.8	31.1	27.2	31.6	37.3	41	45.8	44	52.2	58.5	60.4
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.5	0	0	0	0	0	0	0	0	0
50	Stop1	55.8	55.3	46.9	38.9	30.9	25.5	22.2	19.9	15.1	13.2	56	52.9	44.3	39.4	34.1	27.4	22.6	18.2	17.5	14.9
	Stop2	2.6	2.9	2.4	2.5	1.7	1	0.8	0.3	0.7	0.6	3.3	3.5	2.4	1.4	1.7	1.1	0.7	0.5	0.4	0.7
	Stop3	41.6	41.8	50.7	58.6	67.4	73.5	77	79.8	84.2	86.2	40.5	43.6	53.3	59.2	64.2	71.5	76.7	81.3	82.1	84.4
	Stop4	0	0	0	0	0	0	0	0	0	0	0.2	0	0	0	0	0	0	0	0	0
60	Stop1	44.4	35.9	27.8	20.1	15.6	12.7	8.6	7.1	7.8	3.3	43.6	36.5	26.2	20.7	14.6	9.9	8.8	6.4	4.2	3.2
	Stop2	3.2	2.7	1.6	0.9	0.8	0.7	0.2	0.1	0.2	0.1	3.3	2	1.4	1.8	1.7	0.2	0.2	0.3	0.1	0
	Stop3	52.2	61.4	70.6	79	83.6	86.6	91.2	92.8	92	96.6	52.5	61.5	72.4	77.5	83.7	89.9	91	93.3	95.7	96.8
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.6	0	0	0	0	0	0	0	0	0
70	Stop1	33.5	25.4	17	11.2	6.6	2.8	2	1.2	1.1	0.7	36.7	24	17.3	11.6	5.7	5.2	3.5	1.5	0.7	1.1
	Stop2	2.5	2	1.5	0.4	0.5	0.1	0.3	0.2	0.1	0	2.4	1.9	1	0.5	0.2	0.2	0	0.1	0	0
	Stop3	63.8	72.6	81.5	88.4	92.9	97.1	97.7	98.6	98.8	99.3	60.5	74.1	81.7	87.9	94.1	94.6	96.5	98.4	99.3	98.9
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.4	0	0	0	0	0	0	0	0	0
80	Stop1	29.8	13.5	10	5.1	2.9	1.2	0.3	0.4	0	0.1	27.9	18.6	8.4	4	2.5	1.4	0.9	0.4	0.2	0.1
	Stop2	1.9	1.4	0.3	0.4	0.1	0	0	0.1	0	0	2.5	0.8	0.5	0.2	0.1	0.2	0	0	0	0
	Stop3	68.1	85.1	89.7	94.5	97	98.8	99.7	99.5	100	99.9	68.8	80.6	91.1	95.8	97.4	98.4	99.1	99.6	99.8	99.9
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.8	0	0	0	0	0	0	0	0	0
90	Stop1	22.4	10.5	3.9	1.7	0.7	0.1	0.3	0.2	0	0	20.8	10.2	4.5	3.1	0.7	0.2	0.3	0	0	0
	Stop2	1.9	0.6	0.6	0.1	0	0	0	0	0	0	1.6	0.9	0.5	0	0	0.1	0	0	0	0
	Stop3	75.3	88.9	95.5	98.2	99.3	99.9	99.7	99.8	100	100	76.8	88.9	95	96.9	99.3	99.7	99.7	100	100	100
	Stop4	0.4	0	0	0	0	0	0	0	0	0	0.8	0	0	0	0	0	0	0	0	0
100	Stop1	15.6	5.9	1.5	0.9	0.6	0.1	0.1	0	0	0	15.9	6.7	2.6	0.9	0.2	0.1	0.2	0	0	0
	Stop2	1.6	0.7	0.2	0	0	0	0	0	0	0	1.7	0.2	0.2	0.1	0	0	0	0	0	0
	Stop3	82.3	93.4	98.3	99.1	99.4	99.9	99.9	100	100	100	81.4	93.1	97.2	99	99.8	99.9	99.8	100	100	100
	Stop4	0.5	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0

,

Table A10. Computational results for randomly generated instances with the ratio 10%:10%:40%:40% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	99.9	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100
	Stop2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop3	0.1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100
	Stop2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	99.3	100	100	100	100	100	100	100	100	100	99.5	100	100	100	100	100	100	100	100	100
	Stop2	0.2	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
	Stop3	0.5	0	0	0	0	0	0	0	0	0	0.4	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	98.4	99.9	100	100	100	100	100	100	100	100	99	99.9	100	100	100	100	100	100	100	100
	Stop2	0.5	0.1	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
	Stop3	1.1	0	0	0	0	0	0	0	0	0	0.9	0.1	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	97	99.8	99.9	100	100	100	100	100	100	100	96.4	99.8	100	100	100	100	100	100	100	100
	Stop2	0.1	0	0.1	0	0	0	0	0	0	0	0.5	0.2	0	0	0	0	0	0	0	0
	Stop3	2.9	0.2	0	0	0	0	0	0	0	0	3.1	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
50	Stop1	93	99	99.9	99.9	100	100	100	100	100	100	92.8	99.6	99.9	100	100	100	100	100	100	100
	Stop2	1.2	0.5	0.1	0	0	0	0	0	0	0	0.9	0.1	0	0	0	0	0	0	0	0
	Stop3	5.8	0.5	0	0.1	0	0	0	0	0	0	6.3	0.3	0.1	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
60	Stop1	86.6	97.9	99.6	99.5	99.8	99.8	99.8	99.9	100	100	85.8	97.1	99.3	99.6	99.8	99.7	99.9	100	100	100
	Stop2	1.4	0.5	0	0.2	0	0.1	0	0	0	0	1.5	0.4	0	0	0	0	0	0	0	0
	Stop3	12	1.6	0.4	0.3	0.2	0.1	0.2	0.1	0	0	12.7	2.5	0.7	0.4	0.2	0.3	0.1	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
70	Stop1	82.3	92.5	96.7	97.2	98.6	98.1	99	99.2	99.5	99.7	80	92.7	96.5	97.5	97.9	99.2	99.5	99.5	99.8	99.5
	Stop2	1.8	1.1	0.2	0.2	0	0	0.1	0	0	0.1	1.7	0.5	0	0.2	0.1	0	0	0	0	0
	Stop3	15.9	6.4	3.1	2.6	1.4	1.9	0.9	0.8	0.5	0.2	18.3	6.8	3.5	2.3	2	0.8	0.5	0.5	0.2	0.5
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
80	Stop1	71.8	85.9	91.5	93.8	94.4	95.3	95.6	97.7	97.3	98.1	73.1	87.2	91	93.1	95.1	95.9	96.7	97.3	98.1	98.8
	Stop2	1.9	1.2	0.6	0.2	0.5	0	0	0.1	0	0.1	2	0.9	0.2	0.7	0.1	0.2	0	0.3	0	0
	Stop3	26.3	12.9	7.9	6	5.1	4.7	4.4	2.2	2.7	1.8	24.9	11.9	8.8	6.2	4.8	3.9	3.3	2.4	1.9	1.2
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
90	Stop1	63.2	77.8	81.6	84.2	85	88.7	89.9	91.5	93.6	93.6	61.7	77.2	83.3	85	86.4	88	90.4	91.4	92.7	94.4
	Stop2	2.6	1	0.8	1.1	0.2	0.2	0.6	0.2	0.1	0.2	2.6	1.9	0.9	0.2	0.5	0.2	0.1	0.1	0	0.1
	Stop3	34.2	21.2	17.6	14.7	14.8	11.1	9.5	8.3	6.3	6.2	35.7	20.9	15.8	14.8	13.1	11.8	9.5	8.5	7.3	5.5
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
100	Stop1	53.1	66.7	68.3	70.3	74.1	74.1	75.6	78.3	81	84.1	51.8	67	69.8	71	72.5	75.9	75.7	79.6	79.8	80.3
	Stop2	2.1	1.7	0.6	0.8	0.3	0.7	0.3	0.2	0.1	0.3	2.4	0.9	1	0.7	1.1	0.5	0.3	0.6	0.3	0.5
	Stop3	44.8	31.6	31.1	28.9	25.6	25.2	24.1	21.5	18.9	15.6	45.8	32.1	29.2	28.3	26.4	23.6	24	19.8	19.9	19.2
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

,

Table A11. Computational results for randomly generated instances with the ratio 10%:20%:10%:60% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	99.2	99.6	99.8	100	99.9	100	100	100	100	100	98.5	99.8	99.9	99.9	100	100	100	100	100	100
	Stop2	0	0.1	0.2	0	0.1	0	0	0	0	0	0.2	0.1	0.1	0.1	0	0	0	0	0	0
	Stop3	0.8	0.3	0	0	0	0	0	0	0	0	1.3	0.1	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	98.1	99.2	99.4	99.9	99.9	99.8	100	100	100	100	96.4	99.2	99.8	99.7	99.8	99.9	99.9	100	100	100
	Stop2	0.1	0.5	0.4	0.1	0.1	0	0	0	0	0	0.6	0.3	0.2	0.1	0	0.1	0.1	0	0	0
	Stop3	1.8	0.3	0.2	0	0	0.2	0	0	0	0	3	0.5	0	0.2	0.2	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	91.3	97.7	97.7	97.8	99.1	98.7	98.8	98.7	99.1	99.6	90.3	96.5	97.6	98	98.4	99.1	99.4	99.4	99.2	99
	Stop2	1.4	0.8	0.8	0.7	0.4	0.7	0.4	0.4	0.1	0.1	0.3	1.3	1.4	0.9	0.7	0.6	0.1	0	0.6	0.3
	Stop3	7.3	1.5	1.5	1.5	0.5	0.6	0.8	0.9	0.8	0.3	9.4	2.2	1	1.1	0.9	0.3	0.5	0.6	0.2	0.7
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	83.4	90.5	92	91.4	89.7	90.8	90.4	88.7	88.8	87	82.8	92.2	91.8	92.1	90.5	90.5	88.7	89.8	87.6	86.9
	Stop2	1.7	1.7	1.7	1.1	1.2	1.6	0.6	1.4	1.1	1	1.6	1.2	1.5	0.8	1.5	1.8	0.6	1.2	1.3	1.1
	Stop3	14.8	7.8	6.3	7.5	9.1	7.6	9	9.9	10.1	12	15.6	6.6	6.7	7.1	8	7.7	10.7	9	11.1	12
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	75.8	78.3	76.6	74	72	69.2	65.5	62.7	57.6	59.2	74.3	78.2	78.1	76.3	70.5	68.3	64	65.5	61.2	58.2
	Stop2	1.9	3	3	1.9	1.6	1.4	1.8	1	0.9	1.2	1.6	2.7	2.3	1.3	2.5	1.8	1.7	0.9	1.4	1.5
	Stop3	22	18.7	20.4	24.1	26.4	29.4	32.7	36.3	41.5	39.6	24	19.1	19.6	22.4	27	29.9	34.3	33.6	37.4	40.3
	Stop4	0.3	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
50	Stop1	64.4	65	59.6	53.1	46.9	40.6	40.1	35	31.4	30.4	64.6	63.3	57.6	53.9	49.4	42.6	38.3	36.6	32.4	28
	Stop2	1.9	2.8	1.9	2.1	1.7	1.5	0.8	1.1	1.5	0.7	1.6	3.8	2.4	1.5	1.3	1.1	0.8	1.1	1.3	1.1
	Stop3	33.7	32.2	38.5	44.8	51.4	57.9	59.1	63.9	67.1	68.9	33.6	32.9	40	44.6	49.3	56.3	60.9	62.3	66.3	70.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0.2	0	0	0	0	0	0	0	0	0
60	Stop1	54.4	52.2	42.3	33	28.1	21.7	19.9	15.8	13.7	11.3	54.4	49.2	43.4	33.6	26.7	22.2	20.2	14.9	13	11.1
	Stop2	1.4	2.9	1.8	1.6	1.4	0.7	0.4	0.3	0.2	0.3	2.4	2.4	2.3	2.8	0.9	0.9	0.7	0.4	0.3	0.3
	Stop3	44.1	44.9	55.9	65.4	70.5	77.6	79.7	83.9	86.1	88.4	43	48.4	54.3	63.6	72.4	76.9	79.1	84.7	86.7	88.6
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0.2	0	0	0	0	0	0	0	0	0
70	Stop1	47	37.9	25.3	21	14.1	11	7.5	6	4.4	3.1	44.2	34.1	28.5	19.4	14	11.3	7.5	4.4	4.1	3.1
	Stop2	1.5	1.4	1.3	1.5	0.7	0.5	0.3	0.2	0.1	0	2.1	2.9	1.4	0.7	0.9	0.4	0.1	0.2	0.1	0.1
	Stop3	51.5	60.7	73.4	77.5	85.2	88.5	92.2	93.8	95.5	96.9	53.4	63	70.1	79.9	85.1	88.3	92.4	95.4	95.8	96.8
	Stop4	0	0	0	0	0	0	0	0	0	0	0.3	0	0	0	0	0	0	0	0	0
80	Stop1	38	26.7	16	10.5	6.4	4.9	2.5	1.9	0.8	0.7	35	26.1	17.6	10.4	8.1	4.2	2.2	2.1	1.3	0.5
	Stop2	1.3	1.7	1.3	1	0.9	0.1	0	0.1	0	0	1.6	1.3	0.7	0.7	0.3	0.4	0	0	0	0
	Stop3	60.6	71.6	82.7	88.5	92.7	95	97.5	98	99.2	99.3	63.1	72.6	81.7	88.9	91.6	95.4	97.8	97.9	98.7	99.5
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0.3	0	0	0	0	0	0	0	0	0
90	Stop1	29	15.7	9.2	4.7	3.8	1.7	1.6	0	0.2	0.3	29.5	16.7	10.2	5.9	3.2	2.1	1.1	0.7	0.3	0.2
	Stop2	1.5	1.4	0.7	0.4	0.1	0.2	0.1	0	0	0.1	1.7	1.2	0.4	0.3	0	0	0	0	0	0
	Stop3	69.3	82.9	90.1	94.9	96.1	98.1	98.3	100	99.8	99.6	68.6	82.1	89.4	93.8	96.8	97.9	98.9	99.3	99.7	99.8
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.2	0	0	0	0	0	0	0	0	0
100	Stop1	21.6	12.2	6.7	2.4	1.6	0.6	0.2	0.1	0.1	0	23	11	5.8	3	1.7	0.5	0.2	0.3	0	0
	Stop2	1.2	0.8	0.1	0.1	0.1	0	0	0	0.1	0	1.1	0.6	0.5	0.2	0.1	0	0	0	0	0
	Stop3	77	87	93.2	97.5	98.3	99.4	99.8	99.9	99.8	100	75.3	88.4	93.7	96.8	98.2	99.5	99.8	99.7	100	100
	Stop4	0.2	0	0	0	0	0	0	0	0	0	0.6	0	0	0	0	0	0	0	0	0

,

Table A12. Computational results for randomly generated instances with the ratio 10%:30%:10%:50% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	98.6	99.9	100	100	100	100	100	100	100	100	99.3	100	100	100	100	100	100	100	100	100
	Stop2	0.2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop3	1.2	0.1	0	0	0	0	0	0	0	0	0.7	0	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	97.8	99.4	99.8	99.8	100	99.8	100	100	100	100	97.3	99.7	99.7	100	100	99.9	100	100	99.9	100
	Stop2	0.2	0.1	0.1	0.2	0	0.2	0	0	0	0	0.2	0.1	0.1	0	0	0	0	0	0.1	0
	Stop3	2	0.5	0.1	0	0	0	0	0	0	0	2.5	0.2	0.2	0	0	0.1	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	93.5	98.1	98.1	99.4	99.1	99.7	99.6	99.9	99.7	99.4	95	97.5	98.8	99	99.5	99.5	99.8	99.7	99.6	100
	Stop2	0.4	0.8	0.6	0.2	0.4	0.2	0.2	0.1	0.3	0.2	0.6	0.7	0.6	0.5	0.5	0.3	0.1	0.2	0.3	0
	Stop3	6.1	1.1	1.3	0.4	0.5	0.1	0.2	0	0	0.4	4.4	1.8	0.6	0.5	0	0.2	0.1	0.1	0.1	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	85.9	94.2	96.1	95.2	94.3	95.3	96.1	95.8	95.8	95.2	89.9	94.2	94.2	95.3	95.4	95.9	95.2	95.2	92.8	96.3
	Stop2	0.6	1.4	1.1	1.1	1.2	0.5	0.7	1.1	0.3	0.4	0.9	0.8	1.4	1	1.5	1	1.2	0.6	1.1	0.3
	Stop3	13.5	4.4	2.8	3.7	4.5	4.2	3.2	3.1	3.9	4.4	9.2	5	4.4	3.7	3.1	3.1	3.6	4.2	6.1	3.4
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	80.5	85.7	85.5	83.4	85.4	81.9	82.3	77.7	77.8	77.5	81.7	85.9	88.3	85.6	82.1	84.3	81.6	79.1	80.9	80.1
	Stop2	1.3	2.2	1.9	1.9	1.3	1.4	1.6	1.7	0.7	1.2	1.4	2.2	1.5	2.3	2	1.3	0.4	1.6	1	0.9
	Stop3	18.2	12.1	12.6	14.7	13.3	16.7	16.1	20.6	21.5	21.3	16.9	11.9	10.2	12.1	15.9	14.4	18	19.3	18.1	19
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
50	Stop1	74.1	74.8	72.6	70	67	62	59.2	58.5	54.9	52.7	73	75.9	73.6	69.7	67.6	60.9	62.6	59.1	56.6	52
	Stop2	1.2	2.6	2.5	1.8	1.3	1.5	1.5	0.9	0.9	0.6	0.9	2.1	2.1	1.3	1.2	1.1	0.8	1	0.6	0.4
	Stop3	24.7	22.6	24.9	28.2	31.7	36.5	39.3	40.6	44.2	46.7	26.1	22	24.3	29	31.2	38	36.6	39.9	42.8	47.6
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
60	Stop1	66.9	64.3	60.9	52.3	45	46.7	40	37.4	34.6	32.2	63.8	64.2	58.4	55.9	48.2	42.8	40.1	35.9	36.3	31.2
	Stop2	1.3	3.2	1.6	2.5	1.5	0.9	1.8	0.9	0.8	0.9	0.8	2	1.9	1.6	1.8	1.4	1.2	1.3	0.9	1.3
	Stop3	31.8	32.5	37.5	45.2	53.5	52.4	58.2	61.7	64.6	66.9	35.4	33.8	39.7	42.5	50	55.8	58.7	62.8	62.8	67.5
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
70	Stop1	58.4	52.6	42.7	38.7	34.6	29.4	21.1	21.5	17.6	16.3	57.7	50.8	45	37.9	31	27.6	26.2	21.6	20.5	15.1
	Stop2	1.4	2.2	1	2.3	0.8	0.7	0.5	0.3	0.2	0.1	0.9	3.5	2.4	1.1	1.3	0.6	0.6	0.4	0.3	0
	Stop3	40.2	45.2	56.3	59	64.6	69.9	78.4	78.2	82.2	83.6	41.3	45.7	52.6	61	67.7	71.8	73.2	78	79.2	84.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
80	Stop1	51.9	40.7	34.1	28.3	21.4	14.2	13.9	9.9	9.8	8	49.7	41.7	33.3	27.1	24.1	17.4	14.1	12.6	8.8	7.5
	Stop2	0.9	1.7	1.4	1.4	0.2	0.1	0.2	0.3	0.1	0	0.8	2.5	1.6	0.9	0.5	0.3	0.6	0.5	0	0
	Stop3	47.2	57.6	64.5	70.3	78.4	85.7	85.9	89.8	90.1	92	49.4	55.8	65.1	72	75.4	82.3	85.3	86.9	91.2	92.5
	Stop4	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
90	Stop1	44.2	31.3	24.6	17.3	12.3	11	7.1	4.7	3.6	4.2	44	32.7	24.8	16.3	12.7	10	7.9	6.5	4.2	3.8
	Stop2	1.3	1.3	0.4	0.8	0.2	0.1	0.1	0.1	0.1	0	1	1.4	1.2	1	0.3	0	0.1	0	0.1	0.1
	Stop3	54.5	67.4	75	81.9	87.5	88.9	92.8	95.2	96.3	95.8	54.6	65.9	74	82.7	87	90	92	93.5	95.7	96.1
	Stop4	0	0	0	0	0	0	0	0	0	0	0.4	0	0	0	0	0	0	0	0	0
100	Stop1	36.1	24.3	17.8	12.4	7.5	6.2	3	2.9	2.3	1.1	35.5	25.9	15.3	10.6	6.9	5.1	3.1	2	1.8	1.7
	Stop2	0.8	1.6	0.8	0.6	0.2	0.1	0	0	0.1	0	1	1.1	0.3	0.3	0.2	0	0.1	0	0	0
	Stop3	63.1	74.1	81.4	87	92.3	93.7	97	97.1	97.6	98.9	62.9	73	84.4	89.1	92.9	94.9	96.8	98	98.2	98.3
	Stop4	0	0	0	0	0	0	0	0	0	0	0.6	0	0	0	0	0	0	0	0	0

,

Table A13. Computational results for randomly generated instances with the ratio 10%:40%:10%:40% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	98.9	100	100	100	100	100	100	100	100	100	99.6	99.9	100	100	100	100	100	100	100	100
	Stop2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop3	1.1	0	0	0	0	0	0	0	0	0	0.4	0.1	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	97.6	99.6	99.9	99.9	100	100	100	100	100	100	98.2	99.5	99.9	99.9	100	100	100	99.9	100	100
	Stop2	0	0	0.1	0.1	0	0	0	0	0	0	0	0	0.1	0.1	0	0	0	0.1	0	0
	Stop3	2.4	0.4	0	0	0	0	0	0	0	0	1.8	0.5	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	95.8	98.6	99	99.7	99.7	99.9	99.7	100	100	99.9	95.5	97.6	99.7	99.3	99.5	99.8	100	99.8	99.9	100
	Stop2	0	0.4	0.4	0.1	0.3	0.1	0.2	0	0	0.1	0.1	0.4	0	0.5	0.2	0.2	0	0.1	0.1	0
	Stop3	4.2	1	0.6	0.2	0	0	0.1	0	0	0	4.4	2	0.3	0.2	0.3	0	0	0.1	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	93.2	94.8	97.1	97.8	98.1	98.9	99	99	98.5	99.3	93.4	94.9	96.8	98.3	98.5	97.4	98.8	99.4	99.1	99
	Stop2	0	0.8	0.5	0.9	0.2	0.1	0	0.4	0.5	0.1	0.5	1	0.7	0.3	0.4	0.9	0.2	0.1	0.5	0
	Stop3	6.8	4.4	2.4	1.3	1.7	1	1	0.6	1	0.6	6.1	4.1	2.5	1.4	1.1	1.7	1	0.5	0.4	1
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	88.6	91.1	91	91.9	94.5	91.2	91.7	92	93.3	93	87.7	90.5	91.6	92	92.5	93	93.1	92.6	92	91.5
	Stop2	0.3	1.4	1.1	0.7	0.2	0.8	0.9	0.7	0.9	0.5	0.2	1.7	1	1.3	0.8	0.4	0.9	0.6	0.4	0.7
	Stop3	11.1	7.5	7.9	7.4	5.3	8	7.4	7.3	5.8	6.5	12.1	7.8	7.4	6.7	6.7	6.6	6	6.8	7.6	7.8
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
50	Stop1	84.6	86.9	84.6	84.8	81	82	79.3	79.7	77.8	77.8	85	84.9	82	81.6	82	83.1	77.2	79.7	78.5	78.1
	Stop2	0.6	0.9	1.2	1.6	1.6	1.1	1	0.8	1.1	0.9	0	2.2	1.8	2	1	1.2	1.3	0.9	1.1	1
	Stop3	14.8	12.2	14.2	13.6	17.4	16.9	19.7	19.5	21.1	21.3	15	12.9	16.2	16.4	17	15.7	21.5	19.4	20.4	20.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
60	Stop1	79.7	77.8	75.4	71.5	71.1	69.2	63.5	61.3	59	58.8	77.5	75.1	75.4	71.8	70.7	66.4	66.3	63.5	60.1	60.3
	Stop2	0.2	1.9	2	1.9	1.9	1.2	0.8	1.1	0.9	0.6	0.8	1.7	2.1	1.5	1.4	1.8	0.5	0.8	1.7	1
	Stop3	20.1	20.3	22.6	26.6	27	29.6	35.7	37.6	40.1	40.6	21.7	23.2	22.5	26.7	27.9	31.8	33.2	35.7	38.2	38.7
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
70	Stop1	73.5	68.5	65.8	65.9	57.7	54.2	49.6	47.9	44.8	45.3	75.4	71.4	65.7	62.8	59.4	55.9	50.7	49.5	44.6	43.2
	Stop2	0.6	1.7	1.6	1.4	1.5	0.7	0.9	0.7	0.7	0.8	0.2	1.5	1.2	1.2	1.4	0.7	1	0.7	1	0.7
	Stop3	25.9	29.8	32.6	32.7	40.8	45.1	49.5	51.4	54.5	53.9	24.3	27.1	33.1	36	39.2	43.4	48.3	49.8	54.4	56.1
	Stop4	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
80	Stop1	67.6	60.5	58.7	52.8	46.1	43.5	40.1	36.7	35.4	34.2	66.6	62.4	53.4	50.8	49	43	41.4	37.8	38.7	33.7
	Stop2	0.3	2.7	1.2	1.1	0.9	0.6	0.8	0.4	0.2	0.6	0.4	2.1	2	1.1	1.4	1	0.4	0.3	0.3	0.2
	Stop3	32.1	36.8	40.1	46.1	53	55.9	59.1	62.9	64.4	65.2	32.9	35.5	44.6	48.1	49.6	56	58.2	61.9	61	66.1
	Stop4	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0	0
90	Stop1	63.3	50.9	49.5	42.8	36.3	36.2	33.7	28.7	28.2	28.9	58.2	54.1	51.9	44.1	37.3	33.8	31.6	30.8	27	27.5
	Stop2	0.8	1.5	1.7	0.9	0.5	0.1	0.3	0.2	0.2	0.3	0.3	1.4	1.2	1	0.7	0.5	0.4	0.1	0.3	0
	Stop3	35.9	47.6	48.8	56.3	63.2	63.7	66	71.1	71.6	70.8	41.5	44.5	46.9	54.9	62	65.7	68	69.1	72.7	72.5
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
100	Stop1	58.1	48.4	41.1	32.5	30.9	27.2	24.2	21.2	23.1	20.4	55.5	44.4	38.2	32.2	32.3	27.7	24.1	21.8	22.4	20.3
	Stop2	0.2	1	0.6	0.8	0.3	0.4	0.2	0.4	0	0	0.7	1.5	0.7	0.8	0.6	0.5	0.2	0.1	0.2	0
	Stop3	41.6	50.6	58.3	66.7	68.8	72.4	75.6	78.4	76.9	79.6	43.8	54.1	61.1	67	67.1	71.8	75.7	78.1	77.4	79.7
	Stop4	0.1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

,

Table A14. Computational results for randomly generated instances with the ratio 10%:60%:10%:20% of the numbers of jobs in the subsets ${\mathcal{J}}_1$, ${\mathcal{J}}_2$, ${\mathcal{J}}_{1,2}$ and ${\mathcal{J}}_{2,1}$ of the job set $\mathcal{J}$.

		Uniform Distributions										Gamma Distributions
$\mathbf{\delta }\%$	$\mathit{n}$	10	20	30	40	50	60	70	80	90	100	10	20	30	40	50	60	70	80	90	100
5	Stop1	100	99.8	100	100	100	100	100	100	100	100	100	99.9	100	100	100	100	100	100	100	100
	Stop2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop3	0	0.2	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	Stop1	100	99.9	100	100	100	100	100	100	100	100	100	99.8	99.9	100	100	100	100	100	100	100
	Stop2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Stop3	0	0.1	0	0	0	0	0	0	0	0	0	0.2	0.1	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	Stop1	100	99.4	99.9	100	100	100	100	100	100	100	100	99.3	99.9	100	100	100	100	100	100	100
	Stop2	0	0	0	0	0	0	0	0	0	0	0	0	0.1	0	0	0	0	0	0	0
	Stop3	0	0.6	0.1	0	0	0	0	0	0	0	0	0.7	0	0	0	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
30	Stop1	99.9	98.7	99.7	99.9	100	100	100	100	100	100	100	98.6	99.5	99.5	99.9	100	100	100	100	100
	Stop2	0	0.3	0	0	0	0	0	0	0	0	0	0.2	0.1	0.3	0	0	0	0	0	0
	Stop3	0.1	1	0.3	0.1	0	0	0	0	0	0	0	1.2	0.4	0.2	0.1	0	0	0	0	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
40	Stop1	100	97.3	99.5	99.7	99.7	100	99.8	100	99.9	99.9	100	97.2	98.6	99.1	99.8	100	100	100	99.9	100
	Stop2	0	0.3	0.3	0	0	0	0.1	0	0	0	0	0.1	0.5	0.2	0	0	0	0	0	0
	Stop3	0	2.4	0.2	0.3	0.3	0	0.1	0	0.1	0.1	0	2.7	0.9	0.7	0.2	0	0	0	0.1	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
50	Stop1	99.9	96.1	97	98.3	99.2	99	99.3	99.5	99.8	100	100	95.8	96.9	98.4	99.2	99.2	99.7	99.9	99.6	100
	Stop2	0	0.2	0.5	0.2	0.3	0.5	0.2	0	0.2	0	0	0.2	0.5	0.4	0	0	0.1	0	0	0
	Stop3	0.1	3.7	2.5	1.5	0.5	0.5	0.5	0.5	0	0	0	4	2.6	1.2	0.8	0.8	0.2	0.1	0.4	0
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
60	Stop1	99.7	94.6	96.1	96.8	97.8	98.2	97.9	98.3	98.7	99	99.8	94.9	95.3	97.6	97.9	98.3	96.9	98.8	98.4	98.6
	Stop2	0	0.4	1.1	0.1	0.3	0.2	0.7	0	0.1	0.1	0	0.1	0.2	0.3	0.2	0.3	0.6	0.3	0.4	0.2
	Stop3	0.3	5	2.8	3.1	1.9	1.6	1.4	1.7	1.2	0.9	0.2	5	4.5	2.1	1.9	1.4	2.5	0.9	1.2	1.2
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
70	Stop1	99.6	94.4	94.2	94.8	95.9	94.6	95.6	95.8	96.5	96.7	99.6	94	94.9	93.4	94.5	96	97	96.2	96	96
	Stop2	0	0.4	0.6	0.5	0.6	0.6	0.3	0.4	0.4	0	0	0.2	0.7	0.5	0.4	0.8	0.2	0.2	0.4	0.3
	Stop3	0.4	5.2	5.2	4.7	3.5	4.8	4.1	3.8	3.1	3.3	0.4	5.8	4.4	6.1	5.1	3.2	2.8	3.6	3.6	3.7
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
80	Stop1	99.8	90.9	92	91.2	91.2	92	92	92.3	91.9	92	99.1	89.5	92	91.6	90.8	92.6	92.4	93.4	92.6	92.1
	Stop2	0	0.2	0.6	0.8	0.7	0.2	0.5	0.6	0.4	0.3	0	0.4	0.6	0.7	1.1	0.6	0.5	0.2	0.4	0.1
	Stop3	0.2	8.9	7.4	8	8.1	7.8	7.5	7.1	7.7	7.7	0.9	10.1	7.4	7.7	8.1	6.8	7.1	6.4	7	7.8
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
90	Stop1	98.9	88.3	89.5	88.3	87.6	89	86.1	87.8	86.9	86.2	98.6	89.9	87.3	88.8	88.5	88.7	87.8	85.1	88.5	87.2
	Stop2	0	0.2	1	0.9	1.2	0.5	0.8	0.6	0.2	0.3	0	0.1	0.5	0.3	0.4	0.5	0.7	0.4	0.6	0.9
	Stop3	1.1	11.5	9.5	10.8	11.2	10.5	13.1	11.6	12.9	13.5	1.4	10	12.2	10.9	11.1	10.8	11.5	14.5	10.9	11.9
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
100	Stop1	97.8	88.4	86.6	83.1	85.7	83.4	82.8	81.3	82.1	82.4	97.6	90.2	84.4	85	84.2	81.7	80.2	82.2	80.7	83.2
	Stop2	0	0.4	1.1	1	1	0.6	0.7	0.5	0.8	0.2	0	0.2	0.7	0.9	1.2	0.6	0.6	0.5	0.4	0.5
	Stop3	2.2	11.2	12.3	15.9	13.3	16	16.5	18.2	17.1	17.4	2.4	9.6	14.9	14.1	14.6	17.7	19.2	17.3	18.9	16.3
	Stop4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

present the computational results obtained for the tested classes of instances with the following ratios (28):

$0\%:0\%:10\%:90\%$ (class 1, Table A1); $0\%:0\%:20\%:80\%$ (class 2, Table A2);

$0\%:0\%:30\%:70\%$ (class 3, Table A3); $0\%:0\%:40\%:60\%$ (class 4, Table A4);

$0\%:0\%:50\%:50\%$ (class 5, Table A5); $5\%:5\%:5\%:85\%$ (class 6, Table A6);

$5\%:15\%:5\%:75\%$ (class 7, Table A7); $5\%:20\%:5\%:70\%$ (class 8, Table A8);

$10\%:10\%:10\%:70\%$ (class 9, Table A9); $10\%:10\%:40\%:40\%$ (class 10, Table A10);

$10\%:20\%:10\%:60\%$ (class 11, Table A11); $10\%:30\%:10\%:50\%$ (class 12, Table A12);

$10\%:40\%:10\%:40\%$ (class 13, Table A13); $10\%:60\%:10\%:20\%$ (class 14, Table A14).

All Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11, Table A12, Table A13, Table A14 are organized as follows. The procedure for generating factual processing times (the uniform distribution or the gamma distribution) is indicated in the first row of each table. Numbers n of the given jobs $\mathcal{J}$ in the tested instances of the problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ are presented in the second row. The maximum possible errors $\delta$ of the randomly generated processing times (in percentages) are presented in the first column. For the fixed maximum possible error $\delta$, the obtained computational results are presented in four rows called Stop1, Stop2, Stop3 and Stop4.

The row Stop1 determines the percentage of instances from the tested series, which were optimally solved at the off-line phase of scheduling using either Algorithms 1 or 2 developed in [8]. For such an instance, an optimal pair $({\pi }^{\prime },{\pi }^{″})$ of the job permutations was constructed before the time-point of starting the first job of the realized schedule, i.e., the equality $C_{max}({\pi }^{\prime },{\pi }^{″})=C_{max}({\pi }^{*},{\pi }^{**})$ holds, where $({\pi }^{*},{\pi }^{**}) \in S$ is an optimal pair of job permutations for the deterministic problem $J2|p^{*},n_i\le 2|C_{max}$ with the factual scenario $p^{*} \in T$ that is unknown before completing the whole jobs $\mathcal{J}$.

The row Stop2 determines the percentage of instances, which were optimally solved at the on-line phase of scheduling using corresponding Algorithms 3, 4 or 5. For each such an instance, an optimal pair $({\pi }^{\prime },{\pi }^{″})$ of job permutations for the deterministic problem $J2|p^{*},n_i\le 2|C_{max}$ associated with the factual scenario $p^{*} \in T$ was constructed by checking sufficient conditions in Theorem 9 or Theorem 10. Remind that the factual scenario $p^{*} \in T$ for the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ remains unknown until completing the jobs $\mathcal{J}$.

The row Stop3 determines the percentage of instances, which were optimally solved at the on-line phase of scheduling using Algorithms 3, 4 or 5. In such a case, an optimal pair of job permutations has been constructed for the factual scenario $p^{*} \in T$. However, the optimality of this pair of job permutations was established only after the execution of the constructed schedule.

The row Stop4 determines the percentage of instances, for which the constructed and realized schedule is not optimal for the deterministic instance $J2|p^{*},n_i\le 2|C_{max}$ with the factual scenario $p^{*}$.

6.4. Computational Results

First of all, it is important to determine a total number of the tested instances, for which 3 (or Algorithms 4 and 5) were completed at Step 18 (STOP 2) or at Step 17 (STOP 3). This number shows how many tested instances of the uncertain job-shop scheduling problem have been optimally solved either with the proofs of their optimality before the completion of processing all jobs $\mathcal{J}$ (STOP 2) or the optimality of the obtained schedule was established after the realization of the constructed schedule (STOP 3). For the numbers of jobs from $n=10$ to $n=100$ and for each value of the tested errors $\delta$ of the processing times, average percentages of the instances optimally solved by Algorithms 1, 2, 3, 4 or 5 (these average percentages summarize the values given in rows Stop1 and Stop2 in all Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11, Table A12, Table A13, Table A14) are presented in

Table 2. Average percentages of the instances whose optimality of the constructed permutations was proven at the off-line and on-line phases of scheduling.

$\mathit{\delta }\%$	$5\%$	$10\%$	$20\%$	$30\%$	$40\%$	$50\%$	$60\%$	$70\%$	$80\%$	$90\%$	$100\%$
$0\%:0\%:10\%:90\%$	98.38	95.66	74.32	40.09	18.56	8.65	4.4	2.48	1.58	0.95	0.57
$0\%:0\%:20\%:80\%$	99.48	98.81	94.37	74.52	45.33	24.20	12.32	6.55	3.87	2.59	1.65
$0\%:0\%:30\%:70\%$	99.87	99.71	98.99	95.09	81.33	59.33	36.65	21.67	11.93	7.28	4.39
$0\%:0\%:40\%:60\%$	99.97	99.94	99.73	99.02	97.09	90.86	78.5	59.76	40.85	25.93	15.2
$0\%:0\%:50\%:50\%$	100	99.99	99.93	99.73	99.13	97.55	94.21	86.65	72.35	51.41	29.45
$5\%:5\%:5\%:85\%$	99.67	98.45	78.97	43.19	19.26	9.11	4.31	2.02	1.1	0.58	0.27
$5\%:15\%:5\%:75\%$	99.64	98.86	84.44	51.06	24.65	11.88	6.43	3.34	1.95	1.02	0.68
$5\%:20\%:5\%:70\%$	99.57	98.97	86.92	55.79	29.59	14.98	7.97	4.42	2.59	1.45	1.01
$10\%:10\%:10\%:70\%$	99.84	99.48	97.46	83.55	57.09	34.11	18.95	11.14	6.81	4.29	2.8
$10\%:10\%:40\%:40\%$	99.99	100	99.96	99.89	99.69	99.35	98.41	96.55	92.84	85.66	73.22
$10\%:20\%:10\%:60\%$	99.87	99.68	98.37	90.56	71.05	48.26	30.28	18.22	11.36	7.21	4.79
$10\%:30\%:10\%:50\%$	99.9	99.72	99.11	95.33	83.85	66.15	49.34	34.35	24.13	16.64	11.44
$10\%:40\%:10\%:40\%$	99.92	99.75	99.33	97.97	92.52	82.69	70.01	58.6	48.52	40.36	32.76
$10\%:60\%:10\%:20\%$	99.98	99.98	99.93	99.83	99.59	99.01	97.96	96.16	93.01	89.46	85.75

and Figure 5.

Table 2 shows the total percentages of the optimally solved instances for all classes of the tested instances, for which the optimal schedules were constructed either at the off-line phase of scheduling (STOP 1) or at the on-line phase of scheduling (STOP 2). One can see that for three small values of the maximal errors $\delta \in \{5\%,10\%,20\%$} for most classes, more than $90\%$ (up to $100\%$) of the tested instances were optimally solved. For all tested classes with a maximal error $\delta \le 20\%,$ more than $70\%$ tested instances were optimally solved at the off-line or on-line phases of scheduling.

With a further increasing of the maximal error $\delta$, the percentage of solved instances drops rapidly. For most tested classes with the maximal error $\delta$ greater than $70\%$, the percentage of solved instances is less than $10\%$. However, these indicators differ for different tested classes. For classes 4, 5, 10, 13 and 14 with maximal errors $\delta \le 70\%$, more than $60\%$ of the tested instances were optimally solved with the proof of the optimality before completing all the jobs. The best computational results are obtained for classes 5, 10 and 14 of the tested instances. More than $80\%$ of the instances from these three classes were optimally solved at the off-line phase of scheduling or at the on-line phases of scheduling provided that the maximal error $\delta$ of the given job processing times was no greater than $70\%$, i.e., for $\delta \in \{5\%,10\%,15\%,20\%,30\%,40\%,50\%,60\%,70\%\}$. For both classes 10 and 14 of the tested instances even with an error $\delta =100\%$, more than $70\%$ of the instances were optimally solved.

On the other hand, for both classes 1 and 6 with a maximal error $\delta =40\%$, only less than $20\%$ of the tested instances were optimally solved at both off-line phase and on-line phase of scheduling. For classes 1 and 6 with $\delta =50\%$, less than $10\%$ of the tested instances were optimally solved. Furthermore, these two classes of instances are most difficult ones to find an optimal schedule with the proof of its optimality before completing all the jobs using the on-line phase and off-line phase of scheduling. It should be noted that all tested classes of instances demonstrate a monotonic decrease in the percentages of the optimally solved problems with an increase of the values of the maximal error $\delta$ of the job processing times; see Figure 5.

Let us consider the percentages of the tested instances, for which the optimality of the constructed schedules was proven at the on-line phase of scheduling and the proofs of their optimality being obtained before completing all the jobs. Note that it is novelty of this paper; see rows Stop2 in Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11, Table A12, Table A13, Table A14. For all tested numbers of the jobs, $n \in \{10,20,\cdots ,100\}$, and for all maximal values of the errors $\delta \in \{5\%,10\%,20\%,\cdots ,100\%\}$ of the job processing times, the average percentages of the instances, which were optimally solved by Algorithms 3, 4 or 5 at the on-line phase of scheduling are presented in

Table 3. Average percentages of the instances whose optimality of the constructed permutations was proven at the on-line phase of scheduling.

$\mathit{\delta }\%$	$5\%$	$10\%$	$20\%$	$30\%$	$40\%$	$50\%$	$60\%$	$70\%$	$80\%$	$90\%$	$100\%$
$0\%:0\%:10\%:90\%$	0.97	3.68	8.69	7.26	3.86	1.92	1.06	0.5	0.34	0.2	0.11
$0\%:0\%:20\%:80\%$	0.24	1.24	5.23	8.59	7.85	5.33	2.63	1.49	0.78	0.59	0.32
$0\%:0\%:30\%:70\%$	0.03	0.22	1.33	4.27	6.82	8.13	5.78	4	2.49	1.66	1.07
$0\%:0\%:40\%:60\%$	0.02	0.06	0.31	0.93	2.05	4.15	5.57	6.53	5.6	4.44	3.23
$0\%:0\%:50\%:50\%$	0	0.01	0.06	0.25	0.53	1.24	2.62	4.33	6.06	7.4	6.23
$5\%:5\%:5\%:85\%$	0.33	1.01	2.96	2.31	1.63	0.88	0.49	0.25	0.15	0.07	0.03
$5\%:15\%:5\%:75\%$	0.27	0.84	2.64	2.39	1.78	0.93	0.47	0.3	0.19	0.09	0.08
$5\%:20\%:5\%:70\%$	0.28	0.69	2.38	2.86	1.76	1.07	0.6	0.46	0.26	0.12	0.04
$10\%:10\%:10\%:70\%$	0.06	0.165	0.83	1.87	1.95	1.56	1.08	0.69	0.43	0.32	0.24
$10\%:10\%:40\%:40\%$	0	0	0.02	0.04	0.05	0.14	0.21	0.3	0.45	0.68	0.77
$10\%:20\%:10\%:60\%$	0.05	0.13	0.6	1.29	1.77	1.6	1.22	0.82	0.57	0.41	0.25
$10\%:30\%:10\%:50\%$	0.01	0.07	0.36	0.91	1.49	1.32	1.48	1.03	0.7	0.48	0.36
$10\%:40\%:10\%:40\%$	0	0.03	0.16	0.41	0.78	1.17	1.29	1.01	0.9	0.62	0.46
$10\%:60\%:10\%:20\%$	0	0	0.01	0.05	0.08	0.17	0.28	0.38	0.45	0.51	0.59

, where only Stop2 is indicated.

It should be noted that the monotonous increase of the percentages of the optimally solved instances takes place only for classes 10 and 14 of the tested instances. For other tested classes of instances, there is a maximum, and for the different classes of the tested instances, these maximal vales being achieved for different maximal values of the errors $\delta$. Then the percentages of the optimally solved instances decrease again with the increasing of the maximal values $\delta$. The values of the maximal numbers of instances, which optimal solutions have been proven at the on-line phase of scheduling (STOP 2), vary from $0.59\%$ to $8.69\%$ for different classes of instances.

Classes 1–5 are distinguished from the above classes since their maximal numbers of the instances optimally solved at the on-line phase of scheduling vary from $6\%$ to $9\%$. Average percentages of the instances from these five classes, which were optimally solved by Algorithms 3, 4 or 5 at the on-line phase of scheduling (only Stop2) are shown in Figure 6.

Note that for the difficult classes 1 and 6, the percentages of instances, which were optimally solved at the on-line phase of scheduling with the proofs of their optimality, behave identically with the reaching of the maximum for the maximal error $\delta =20\%$. However their maximal values differ, namely: from $2.96\%$ for class 6 up to $8.69\%$ for class 1.

For the instances, for which the optimality of the constructed schedules was not proven before completing all the jobs $\mathcal{J}$, the relative errors $\Delta \%$ of the achieved objective function vales for the realized schedules were calculated. Note that the positive errors $\Delta \%$ may occur only if Algorithm 3 (or Algorithms 4 and 5) have been stopped at Step 16; see STOP 4. For all tested numbers of jobs $n \in \{10,20,\cdots ,100\}$ and for all maximal values of the errors $\delta \in \{5\%,10\%,20\%,\cdots ,100\%\}$ of the job processing times, the maximal values of ${\Delta }_{max}\%$ and the average values of ${\Delta }_{ave}\%$ were calculated separately for instances with uniform distributions (see

Table 4. Maximal errors ${\Delta }_{max}$ and average errors ${\Delta }_{ave}$ for all tested instances with factual processing times randomly generated based on a uniform distribution.

Class	$\mathit{\delta }\%$	$5\%$	$10\%$	$20\%$	$30\%$	$40\%$	$50\%$	$60\%$	$70\%$	$80\%$	$90\%$	$100\%$
1	${\Delta }_{max}$	0.031511	0.300924	0.691062	0.333292	1.110492	0.881902	2.246299	3.263145	2.729286	3.85936	5.024917
	${\Delta }_{ave}$	0.000003	0.000058	0.000225	0.000057	0.000333	0.000613	0.000733	0.00135	0.001868	0.001409	0.002253
2	${\Delta }_{max}$	0.0475	0.189872	0	0.125467	0	0.441669	0.243659	1.076096	3.127794	1.286158	1.353086
	${\Delta }_{ave}$	0.000005	0.000023	0	0.000013	0	0.000064	0.000045	0.000189	0.000976	0.000221	0.000135
3	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0.8199	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0.000082	0	0
4	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0
5	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0
6	${\Delta }_{max}$	0	0	0	0	0	0.411415	0.081623	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0.000082	0.000016	0	0	0	0
7	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0
8	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0
9	${\Delta }_{max}$	0	0.068237	0.055299	0	1.31253	0	0.91223	0.893705	1.697913	2.166717	8.617851
	${\Delta }_{ave}$	0	0.000007	0.000006	0	0.000244	0	0.000144	0.000167	0.000338	0.000558	0.001348
10	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0
11	${\Delta }_{max}$	0	0	0	1.47875	3.660297	5.724288	0.810014	3.316178	0.39653	4.42828	4.666154
	${\Delta }_{ave}$	0	0	0	0.000148	0.000694	0.000572	0.000081	0.000332	0.000040	0.000799	0.000924
12	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	7.243838
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0.000724
13	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	5.036085
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0.000504
14	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0

) and gamma distributions (see

Table 5. Maximal errors ${\Delta }_{max}$ and average errors ${\Delta }_{ave}$ for all tested instances with factual processing times randomly generated based on a gamma distribution.

Class	$\mathit{\delta }\%$	$5\%$	$10\%$	$20\%$	$30\%$	$40\%$	$50\%$	$60\%$	$70\%$	$80\%$	$90\%$	$100\%$
1	${\Delta }_{max}$	0.211802	0.509319	1.995284	2.439105	4.8928	2.670648	6.613935	8.782202	10.59834	9.153295	9.50327
	${\Delta }_{ave}$	0.000055	0.000131	0.00031	0.000746	0.001754	0.001746	0.00369	0.005033	0.006755	0.011687	0.01144
2	${\Delta }_{max}$	0	0	0	0	0	4.182544	1.361694	1.070905	5.634459	7.845669	7.974282
	${\Delta }_{ave}$	0	0	0	0	0	0.000595	0.000317	0.000107	0.001382	0.001737	0.001725
3	${\Delta }_{max}$	0	0	0	0	1.32533	0	0	5.566808	0	4.026352	5.385314
	${\Delta }_{ave}$	0	0	0	0	0.000133	0	0	0.000557	0	0.000511	0.001354
4	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	6.044646	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0.000604	0
5	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0
6	${\Delta }_{max}$	0	0	0	0.061048	0	0.387884	1.081353	1.125343	0.710307	0.643768	0.67762
	${\Delta }_{ave}$	0	0	0	0.000012	0	0.000078	0.000216	0.000401	0.000206	0.000343	0.000136
7	${\Delta }_{max}$	0	0	0.143177	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0.000029	0	0	0	0	0	0	0	0
8	${\Delta }_{max}$	0	0	0.388797	0	0.426346	0	0.289505	0.059146	2.478004	1.167724	4.748751
	${\Delta }_{ave}$	0	0	0.000078	0	0.000085	0	0.000029	0.000006	0.000442	0.000234	0.000948
9	${\Delta }_{max}$	2.64165	6.620637	5.266738	4.163808	10.56515	0	0	0	0	0	0
	${\Delta }_{ave}$	0.000852	0.001946	0.001696	0.001615	0.003941	0	0	0	0	0	0
10	${\Delta }_{max}$	0	0	0	0	0	0	0	0.714515	0	0.334513	3.232162
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0.000071	0	0.000033	0.000584
11	${\Delta }_{max}$	2.988951	10.50113	2.526341	5.632594	7.258956	0	0	0	0	0	0
	${\Delta }_{ave}$	0.0003	0.001289	0.000431	0.000887	0.001595	0	0	0	0	0	0
12	${\Delta }_{max}$	0	0.095929	1.639148	17.64929	6.3913	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0.000010	0.000164	0.002948	0.001737	0	0	0	0	0	0
13	${\Delta }_{max}$	0	0.967642	0.7847	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0.000097	0.000078	0	0	0	0	0	0	0	0
14	${\Delta }_{max}$	0	0	0	0	0	0	0	0	0	0	0
	${\Delta }_{ave}$	0	0	0	0	0	0	0	0	0	0	0

).

It can be seen that the values of maximal errors ${\Delta }_{ave}\%$ significantly differ when applying different distribution laws. With using a uniform distribution, the maximal error ${\Delta }_{max}$ does not exceed $9\%$, while when using a gamma distribution, the maximal error ${\Delta }_{max}$ could reach a value more than $17\%$.

It can be seen that for using various distribution laws, Algorithm 3 (Algorithms 4 and 5 as well) terminates at STOP 4 with various combinations of the tested classes and maximal errors $\delta \%$. If a uniform distribution is used, then for classes 1–2, strictly positive errors ${\Delta }_{ave}\%$ arise for all values of the tested maximal errors $\delta \%$. For classes 9–10 and 11–13, such errors appear more often with increasing the maximal error $\delta \%$.

For a gamma distribution, for all values of $\delta \%$, the error ${\Delta }_{ave}\%$ arises only for class 1. For classes 2–4, 6, 8, 10, the error ${\Delta }_{ave}\%$ arises with the growth of maximal errors $\delta \%$. For classes 7, 9, 11–13, on the contrary, the error ${\Delta }_{ave}\%$ is more common for small values of the maximal errors $\delta \%$.

As one can see, using the uniform distribution for the generation of the factual job processing times for classes 4, 5, 7, 10, 14, all tested instances were solved optimally using the developed algorithms and two phases of scheduling. In other words, there are no instances, for which corresponding Algorithms 3, 4 or 5 was stopped at Step 16 (STOP 4). However, for the gamma distribution, there are only two such classes 5 and 14. Thus, classes 5 and 14 can be considered as easy ones, while class 1 is the most difficult one. As for class 1, Algorithms 3, 4 and 5 are stopped at Step 16 (STOP 4) for all values of the tested maximal errors $\delta \%$. Moreover, the maximum makespan error ${\Delta }_{max}\%$ of more than $5\%$ for the uniform distribution and more than $10\%$ for the gamma distribution is found for classes 1, 9, 11 and 12 of the tested instances (these classes are difficult for the used stability approach).

Class 13 of the tested instances is a rather strange one. For using the uniform distribution, a maximum makespan error ${\Delta }_{max}\%$ of more than $5\%$ was obtained, while when for using the gamma distribution, the maximum makespan error ${\Delta }_{max}\%$ did not reach even $1\%$. Note that for all tested classes of the instances, the average makespan errors ${\Delta }_{ave}\%$ for all tested numbers $n \in \{10,20,\cdots ,100\}$ of jobs $\mathcal{J}$ are less than $0.02\%$.

Maximal relative makespan errors ${\Delta }_{max}\%$ for each tested class and for all values of the tested maximal errors $\delta$ are shown in Figure 7 for the instances with uniform distributions and in Figure 8 for the instances with gamma distributions of the factual durations of the given operations.

Figure 7 and Figure 8 also show that the maximal value of the makespan errors ${\Delta }_{max}\%$ for the constructed and realized schedule for the factual scenarios are achieved for different values of the maximal errors $\delta \%$ for different classes of the tested instances.

7. Concluding Remarks

The uncertain job-shop scheduling problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ attract the attention of practitioners and researchers since this problem is applicable in real-life processing systems for some reduction of production costs due to a better utilization of the available machines and resources.

This paper is a continuation of our previous one [8], where only off-line phase of scheduling was investigated and tested for the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ based on the stability approach. In [8], we tested 15 classes of the randomly generated instances $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. A lot of instances from nine easy classes were optimally solved at the off-line phase of scheduling. If the maximal errors were no greater than $20\%$, i.e., $\delta \in \{5\%,10\%,15\%,20\%\}$, then more than $80\%$ of the tested instances were optimally solved at the off-line phase of scheduling. If the maximal error was equal to $50\%$, i.e., $\delta =50\%$, then $45\%$ of the tested instances were optimally solved.

However, less than $5\%$ of the tested instances with maximal possible error $\delta \ge 20\%$ from six hard tested classes were optimally solved at the off-line phase of scheduling. There were no tested hard instances with the maximal error $50\%$ optimally solved in [8]. All these difficulties were succeeded in Section 4, Section 5 and Section 6 of this paper, where it is shown that the on-line phase of scheduling allows a scheduler to find either optimal schedule or very close to optimal ones. Additional information on the factual value of the job processing times becomes available once the processing of the job on the machine is completed. Using this information, a scheduler can determine a smaller dominant set of semi-active schedules, which is based on sufficient conditions for schedule dominance. The smaller dominant set enables a scheduler to quickly make an on-line scheduling decision whenever additional information on processing the job becomes available.

In Section 5, it is investigated the optimal pair $({\pi }^{\prime },{\pi }^{″})$ of job permutations (Theorems 9 and 10). Using the proven analytical results, we derived Algorithms 3–5 for constructing optimal pairs $({\pi }^{\prime },{\pi }^{″})$ of job permutations for all scenarios $p \in T$ or a small dominant set $S\left(T\right)$ of schedules for the uncertain problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$. At the off-line scheduling phase, Algorithms 1 and 2 [8] are used to determine the partial strict order $A_{\prec }^{1,2}$ over the job set ${\mathcal{J}}_{1,2}$ and the partial strict order $A_{\prec }^{2,1}$ over the job set ${\mathcal{J}}_{2,1}$. The constructed precedence digraphs $({\mathcal{J}}_{1,2},A_{\prec }^{1,2})$ and $({\mathcal{J}}_{2,1},A_{\prec }^{2,1})$ determine a minimal dominant set $S\left(T\right)$ of schedules.

In Section 6, it is shown how to use Algorithms 3–5 for constructing a small dominant set of semi-active schedules that enables a scheduler to make a fast decision whenever information on completing some jobs become available. Based on these algorithms, the problem $J2|l_{ij}\le p_{ij}\le u_{ij},n_i\le 2|C_{max}$ was solved with very small errors of the obtained objective values. The computational experiments (Section 6.3) show that pairs of job permutations constructed by Algorithms 3–5 are very close to the optimal pairs of job permutations. We tested 14 classes of randomly generated instances. For the tested instances, the percentage of the optimally solved instances slowly decreases with increasing maximal errors $\delta$ of the processing times. The developed on-line algorithms perform with the maximal errors of the achieved makespan less than $1\%$ if $n \in \{20,30,\dots ,100\}$. For all tested classes of the instances, the average makespan errors for all numbers $n \in \{10,20,\cdots ,100\}$ of the jobs $\mathcal{J}$ were less than $0.02\%$.

In a possible further research, one can continue the study of the uncertain job-shop scheduling problem based on the stability approach. It is useful to improve the developed algorithms and to extend them for other machine environments, such as a single machine or processing systems with parallel machines. It is promising to investigate an optimality region of the semi-active schedule and to develop algorithms for constructing a semi-active schedule with the largest optimality region.

It is also useful to apply the stability approach for solving the uncertain flow-shop and job-shop scheduling problems with $\left|\mathcal{M}\right|\ge 3$ different machines.