A Novel Framework to Harmonise Satellite Data Series for Climate Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Review of the Single-Sensor Calibration Problem
2.2. Representation of Uncertainty in Matchup Datasets
- Independent random errors—arise from uncorrelated, i.e., independent, random error effects. Each measurement included with exhibits an error that is random and independent from the errors of all other measurements. The error covariance matrix is diagonal with elements that represent the variance of each error. Letdefine the diagonal uncertainty matrix; thus, the error covariance matrix , which is diagonal and of full rank, is given by
- Common random errors—arise from a fully correlated, i.e., common, random error effect. All measurements in exhibit an error that is due to the same random effect e. Let denote the uncertainty associated with this effect and let be the absolute sensitivity of with respect to e. Then, the law of propagation of uncertainty [11] states that the uncertainty of the measurements which results from each such effect e isand that the error covariance matrix , which is dense and of rank one, is given by
- Structured random errors—arise when the measurements in are not original measurements but rather result from an operation on an underlying (and usually larger) set of original measurements of the same quantity q measured at instants , i.e.,and these measurements have independent random errors (case 1) associated with them. A common example operation would be some form of averaging [1,2], but any linear mapping of measurements from to is permissible. Let , where is the matrix that defines the linear operation. Thus, the error covariance matrix , which is typically sparse and of rank , is given by
- Structured common random errors—arise when the measurements in are not original measurements, but result from an operation on an underlying set of original measurements that have both independent random errors (case 1) and systematic errors (case 2) associated with them. Letas in the third case. Here, the error covariance matrix is dense and given bywhich, because , is equivalent to
2.3. Formulation of the Harmonisation Problem
2.3.1. EIV Formulation
2.3.2. Marginalised EIV (MEIV) Formulation
2.4. Measurement Equation
2.5. Satellite Data
3. Results
3.1. Harmonised Calibration Parameters
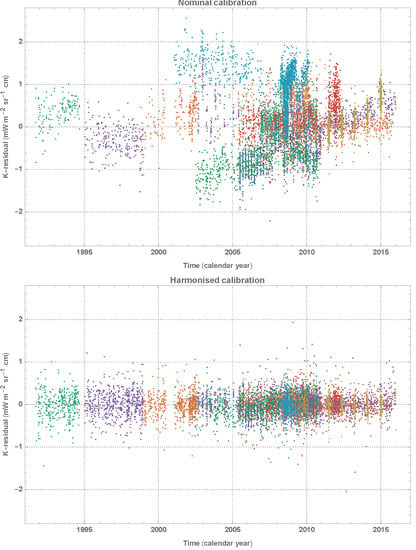
3.2. Diagnostic Diagrams
3.3. Stability of the Calibrated Radiance Data Record
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AATSR | Advanced Along Track Scanning Radiometer |
| AD | Algorithmic Differentiation |
| AVHRR | Advanced Very High Resolution Radiometer |
| BFGS | Broyden–Fletcher–Goldfarb–Shanno |
| CDR | Climate Data Record |
| EIV | Errors-in-Variables |
| ESA | European Space Agency |
| FCDR | Fundamantal Climate Data Record |
| FIDUCEO | Fidelity and Uncertainty in Climate Data Records from Earth Observations |
| GAC | Global Area Coverage |
| GCOS | Global Climate Observing System |
| GSICS | Global Space-based Inter-Calibration System |
| HIRS | High Resolution Infrared Radiation Sounder |
| IASI | Infrared Atmospheric Sounding Interferometer |
| IR | Infrared |
| MEIV | Marginalised Errors-in-Variables |
| NOAA | National Oceanic and Atmospheric Administration |
| SI | International System of Units |
| TOA | Top-of-Atmosphere |
References
- Woolliams, E.R.; Mittaz, J.P.D.; Merchant, C.J.; Hunt, S.E.; Harris, P.M. Applying metrological techniques to satellite fundamental climate data records. J. Phys. Conf. Ser. 2018, 972, 012003. [Google Scholar] [CrossRef]
- Mittaz, J.; Merchant, C.J.; Woolliams, E.R. Applying principles of metrology to historical Earth observations from satellites. Metrologia 2019. [Google Scholar] [CrossRef]
- Merchant, C.J.; Holl, G.; Mittaz, J.P.D.; Woolliams, E.R. Radiance Uncertainty Characterisation to Facilitate Climate Data Record Creation. Remote Sens. 2019, 11, 474. [Google Scholar] [CrossRef]
- Merchant, C.J.; Paul, F.; Popp, T.; Ablain, M.; Bontemps, S.; Defourny, P.; Hollmann, R.; Lavergne, T.; Laeng, A.; de Leeuw, G.; et al. Uncertainty information in climate data records from Earth observation. Earth Syst. Sci. Data 2017, 9, 511–527. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.P.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of intercalibration of satellite instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Newey, W.K. Flexible simulated moment estimation of nonlinear errors-in-variables models. Rev. Econ. Stat. 2001, 83, 616–627. [Google Scholar] [CrossRef]
- Zwolak, J.W.; Boggs, P.T.; Watson, L.T. Algorithm 869: ODRPACK95: A weighted orthogonal distance regression code with bound constraints. ACM Trans. Math. Softw. 2007, 33, 27. [Google Scholar] [CrossRef]
- Hunt, S.E.; Quast, R.; Harris, P.M.; Mittaz, J.P.D.; Woolliams, E.R.; Giering, R.; Dilo, A.; Merchant, C.J. A metrological approach to producing harmonised fundamental climate data records from long-term sensor series data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3397–3400. [Google Scholar]
- Harris, P.M.; Hunt, S.E.; Quast, R.; Giering, R.; Mittaz, J.P.D.; Woolliams, E.R.; Dilo, A.; Cox, M. Solving large structured non-linear least-squares problems with an application in Earth observation. in preparation.
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2005. [Google Scholar]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data. Guide to the Expression of Uncertainty in Measurement (JCGM 100:2008). Available online: http://www.bipm.org/en/publications/guides (accessed on 24 August 2018).
- Griewank, A.; Walther, A. Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, 2nd ed.; Number 105 in Other Titles in Applied Mathematics; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Barrett, R.; Berry, M.; Chan, T.F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1994. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited-memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Morales, J.L.; Nocedal, J. Remark on Algorithm 778: L-BFGS-B: Fortran Subroutines for Large-scale Bound Constrained Optimization. ACM Trans. Math. Softw. 2011, 38, 7:1–7:4. [Google Scholar] [CrossRef]
- Giering, R.; Kaminski, T. Recipes for Adjoint Code Construction. ACM Trans. Math. Softw. 1998, 24, 437–474. [Google Scholar] [CrossRef]
- Giering, R.; Kaminski, T. Applying TAF to generate efficient derivative code of Fortran 77–95 programs. In PAMM: Proceedings in Applied Mathematics and Mechanics; WILEY-VCH: Berlin, Germany, 2002. [Google Scholar]
- Giering, R.; Kaminski, T. Recomputations in Reverse Mode AD. In Automatic Differentiation: From Simulation to Optimization; Corliss, G., Faure, C., Griewank, A., Hascoët, L., Naumann, U., Eds.; Computer and Information Science; Springer: New York, NY, USA, 2002; Chapter 33; pp. 283–291. [Google Scholar]
- Giering, R.; Kaminski, T.; Slawig, T. Generating efficient derivative code with TAF. Future Gener. Comput. Syst. 2005, 21, 1345–1355. [Google Scholar] [CrossRef]
- Giering, R.; Voßbeck, M. Increasing memory locality by executing several model instances simultaneously. In Recent Advances in Algorithmic Differentiation; Forth, S., Hovland, P., Phipps, E., Utke, J., Walther, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 93–101. [Google Scholar]
- NOAA KLM User’s Guide with NOAA-N, N Prime, and MetOp Supplements; National Oceanic and Atmospheric Administration: Washington, DC, USA, 2014.
- Smith, D.; Mutlow, C.; Delderfield, J.; Watkins, B.; Mason, G. ATSR infrared radiometric calibration and in-orbit performance. Remote Sens. Environ. 2012, 116, 4–16. [Google Scholar] [CrossRef]
- Block, T.; Embacher, S.; Merchant, C.J.; Donlon, C. High-performance software framework for the calculation of satellite-to-satellite data matchups (MMS version 1.2). Geosci. Model Dev. 2018, 11, 2419–2427. [Google Scholar] [CrossRef]
- Wu, W.; Hewison, T.; Tahara, Y. GSICS GEO-LEO inter-calibration: Baseline algorithm and early results. In Atmospheric and Environmental Remote Sensing Data Processing and Utilization V: Readiness for GEOSS III; Springer: Berlin/Heidelberg, Germany, 2009; Volume 7456, pp. 745604-1–745604-12. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- NOAA. GCOS Ocean Physics ECV—Sea Surface Temperature. Available online: https://www.ncdc.noaa.gov/gosic/gcos-essential-climate-variable-ecv-data-access-matrix/gcos-ocean-physics-ecv-sea-surface-temperature (accessed on 14 February 2019).
- FastOpt GmbH. Transformation of Algorithms in Fortran Demonstrator. Available online: http://www.fastopt.de/test/taf/tafdemo.html (accessed on 4 April 2019).
- Fidelity and Uncertainty in Climate Data Records from Earth Observation (FIDUCEO). FIDUCEO Web Site. Available online: http://www.fiduceo.eu (accessed on 4 April 2019).
- Global Space-based Inter-Calibration System (GSICS). GSICS Web Site. Available online: https://gsics.wmo.int (accessed on 4 April 2019).








| Generic Name | Specific Name | Descriptive Name | Error Correlation Structure |
|---|---|---|---|
| Space count average | structured random | ||
| ICT count average | structured random | ||
| Earth count | independent random | ||
| ICT radiance | independent random | ||
| T | instrument temperature | independent random |
| Number of Matchups (Million) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| m02 | n19 | n18 | n17 | n16 | n15 | n14 | n12 | n11 | |
| aatsr | 2.40 | 0.23 | 0.61 | 0.26 | 0.70 | 0.19 | - | - | - |
| m02 | - | 2.20 | 2.72 | 2.13 | 1.75 | 1.43 | - | - | - |
| n19 | - | - | 2.19 | 1.25 | 1.50 | 1.30 | - | - | - |
| n18 | - | - | - | 2.26 | 2.64 | 1.45 | - | - | - |
| n17 | - | - | - | - | 2.27 | 1.78 | - | - | - |
| n16 | - | - | - | - | - | 2.09 | - | - | - |
| n15 | - | - | - | - | - | - | 2.27 | - | - |
| n14 | - | - | - | - | - | - | - | 2.38 | - |
| n12 | - | - | - | - | - | - | - | - | 1.40 |
| Satellite | Abbreviation | Calibration Coefficients | |||
|---|---|---|---|---|---|
| MetOp-A | m02 | ||||
| NOAA-19 | n19 | ||||
| NOAA-18 | n18 | ||||
| NOAA-17 | n17 | ||||
| NOAA-16 | n16 | ||||
| NOAA-15 | n15 | ||||
| NOAA-14 | n14 | ||||
| NOAA-12 | n12 | ||||
| NOAA-11 | n11 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giering, R.; Quast, R.; Mittaz, J.P.D.; Hunt, S.E.; Harris, P.M.; Woolliams, E.R.; Merchant, C.J. A Novel Framework to Harmonise Satellite Data Series for Climate Applications. Remote Sens. 2019, 11, 1002. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11091002
Giering R, Quast R, Mittaz JPD, Hunt SE, Harris PM, Woolliams ER, Merchant CJ. A Novel Framework to Harmonise Satellite Data Series for Climate Applications. Remote Sensing. 2019; 11(9):1002. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11091002
Chicago/Turabian StyleGiering, Ralf, Ralf Quast, Jonathan P. D. Mittaz, Samuel E. Hunt, Peter M. Harris, Emma R. Woolliams, and Christopher J. Merchant. 2019. "A Novel Framework to Harmonise Satellite Data Series for Climate Applications" Remote Sensing 11, no. 9: 1002. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11091002