An ENSO Prediction Model Based on Backtracking Multiple Initial Values: Ordinary Differential Equations–Memory Kernel Function

Abstract

This article presents a new prediction model, the ordinary differential equations–memory kernel function (ODE–MKF), constructed from multiple backtracking initial values (MBIV). The model is similar to a simplified numerical model after spatial dimension reduction and has both nonlinear characteristics and the low-cost advantage of a time series model. The ODE–MKF focuses on utilizing more temporal information and includes machine learning to solve complex mathematical inverse problems to establish a predictive model. This study first validates the feasibility of the ODE–MKF via experiments using the Lorenz system. The results demonstrate that the ODE–MKF prediction model could describe the nonlinear characteristics of complex systems and exhibited ideal predictive robustness. The prediction of the El Niño-Southern Oscillation (ENSO) index further demonstrates its effectiveness, as it achieved 24-month lead predictions and effectively improved nonlinear problems. Furthermore, the reliability of the model was also tested, and approximately 18 months of prediction were achieved, which was verified with the Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) radiation fluxes. The short-term memory index Southern Oscillation (SO) was further used to examine the applicability of ODE–MKF. A six-month lead prediction of the SO trend was achieved, indicating that the predictability of complex systems is related to their inherent memory scales.

1. Introduction

The climate is influenced by multiple interactions among oceans, land, ice, and other components. The factors affecting the climate are complex and variable, making climate prediction challenging [1]. Currently, climate prediction has primarily focused on the statistical modeling of time series data. There are two main types of time series prediction models: short-memory models and long-memory models [2]. The short-memory models, represented by moving average (MA) [3] and autoregressive (AR) models [4,5], assume complete independence between samples or exponential decay in the autocorrelation function, but there is a gap between the predictions and actual observations. The long-memory models, such as the fractionally differenced noise (FDN) [6,7] and autoregressive fractionally integrated moving average (ARFIMA) models [8], are designed to capture long-range dependencies. Early prediction models mainly assume that the evolving system is stationary or linear. Other studies have also recognized the importance of nonlinear dependence for time series modeling, such as threshold autoregressive (TAR) [9] and exponential autoregressive (EAR) models [10]. However, these models have strict assumptions and are challenging to use in climate prediction [11,12]. To address the challenges of climate prediction, specialized meteorological time series forecasting models have been developed. Examples of such models include canonical correlation analysis (CCA) [13,14], principal component analysis (PCA) [15], and singular value decomposition (SVD) [16,17]. These mathematical schemes perform better than regression-based methods in climate prediction. However, they still exhibit significant uncertainty when dealing with complex nonlinear problems.

With the successful development of numerical weather and climate models, global climate models (GCMs) have become important tools for studying the mechanisms of climate change and projecting the future climate in recent decades [18,19,20]. Another important method of climate prediction is model downscaling [21,22]. However, the physical parameterization schemes of such models have still not been sufficiently refined [23,24]. Climate models are more complex and require more physical processes [22,23,24,25]. To reduce cumulative errors and better capture extreme events, it is necessary to decrease the temporal and spatial resolutions, which preserves a greater range of climatological dynamical features at different scales. However, this reduction in resolutions can increase computational requirements and uncertainties in the long-term integration process. As a result, the application of downscaling methods to prediction is also limited [20,24]. To improve the forecasting ability of climate prediction, researchers have proposed transforming the initial value problem into an evolutionary problem, which uses observational data to compensate for the deficiencies in the physical parameterization processes of the model, subsequently performing error corrections [26,27]. The results have indicated that this scheme is effective. However, it is still insufficient for significantly improving climate prediction. That is, relying on statistical optimization to further improve model results has limited potential for improving prediction. On one hand, the use of only a single initial value is a fundamental limitation of the model. On the other hand, although statistical methods utilize all historical values, their extrapolation capabilities remain weak [28]. Although combining both methods takes advantage of the historical evolution information, it focuses more on the error correction scheme, and the historical data do not truly participate in the integration of the model [29]. In essence, time series statistical methods based on an additive scheme have inherent limitations in dealing with nonlinear problems.

Considering the excellent capabilities of differential methods in handling nonlinear problems, this study proposes an alternative and flexible nonlinear modeling scheme for time series, which is based on differential equations and incorporates more observational information into the model. The new prediction model, the ordinary differential equations–memory kernel function (ODE–MKF), is gradient-based, utilizing backtracking multiple initial values (BMIV) [30,31]. Additionally, it aims to incorporate the physical mechanisms of the dynamic system into the modeling process and simplify the complexity of nonlinear processes. The main challenges of this scheme are the inversion of time series differential equations and its sensitivity to the initial conditions. Thus, the memory kernel function (MKF) plays a crucial role in the differential equations, which effectively utilizes temporal information and compensates for the missing spatial information due to dimensionality reduction [32,33,34,35,36]. Embedding the MKF into the differential equation and integrating it forms a complex inverse problem in mathematical terms. Meanwhile, this study also uses machine learning methods to intelligently address the aforementioned complex mathematical problems [37,38].

El Niño-Southern Oscillation (ENSO) is the most important coupled ocean–atmosphere phenomenon in the tropical Pacific [38]. The phase changes of ENSO have significant influences on global climate changes [39,40]. Studies have reported that the real-time ENSO prediction capability is still at a moderate level. In recent years, owing to the non-uniformity of global warming, the uncertainty of the climate system has been further enhanced, and the prediction of ENSO has become more complicated [41]. Keppenne and Ghil (1992) described ENSO as a second-order Mathieu/Hill differential equation, and its forcing originates from the tidal motion in the quasi-biennial oscillation (QBO) and the synchronized angular momentum changes with the Chandler wobble [42]. Compared with the Lorenz system, ENSO is much more complex, which introduces additional uncertainties to prediction. Methods and techniques are continuously being developed to understand the ENSO anomalies and to improve ENSO prediction [43]. Statistical ENSO prediction is an alternative with computational efficiency and a lower cost, and further effort is required to decrease prediction uncertainty. Nonlinear methods combined with principal component analysis (PCA) perform well, especially on processes manifesting nonlinear dynamical properties on interannual scales [44]. Furthermore, machine learning methods have been applied for ENSO analysis and prediction, which usually are associated with nonlinear methods [45]. For example, maximum variance unfolding (MVU), a nonlinear method of dimensionality reduction, is one of the variants of kernel PCA based on semidefinite programming. It has been widely used to produce skillful cross-validated forecasts on climate predictions [46]. Better than other dynamical and statistical models, which may overestimate the intensity, nonlinear dimensionality reduction brings potential gain [47]. However, MVU cannot project out-of-sample data onto the feature space or reconstruct test data directly as PCA in ENSO prediction like most nonlinear methods, which remains debatable [48]. Additionally, ODE–MKF, which can perfectly handle nonlinear problems by differential methods and compensate for the missing spatial information, has more advantages in ENSO and other nonlinear processes forecasting.

The used datasets and key methods are described in Section 2, along with the detailed machine learning algorithms for evolutionary modeling. Local and global behaviors in a complex climate system are discussed in Section 3. Studies of the MKF model for Niño3.4 are introduced in Section 4. In Section 5, the influences of the backtracking scale are discussed, and, finally, this method is used to predict ENSO. The final section discusses how the proposed model could be moved into operation and what would be needed to make it work in practice, and some suggestions for future work are proposed.

2. Materials and Methods

2.1. Materials

The data used in this study are the indices for El Niño-Southern Oscillation, particularly Niño3.4 and the Southern Oscillation index (SOI), which can be downloaded from the following NOAA site: https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Nino34/ (accessed on 1 June 2023).

The Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) top-of atmosphere (TOA), Edition 4.1 (Ed4.1) data product is used to verify the correctness of the training and predictions results [49]. In this study, the monthly mean radiative fluxes include the outgoing longwave radiation, incoming solar radiation, and upwelling shortwave radiation at TOA during all-sky and clear-sky conditions between March 2000 and December 2022, with 1° × 1° spatial resolution [50]. Clear-sky fluxes that were calculated by sampling only cloud-free pixels were used and can be downloaded from the following site: https://ceres.larc.nasa.gov/data/ (accessed on 1 June 2023).

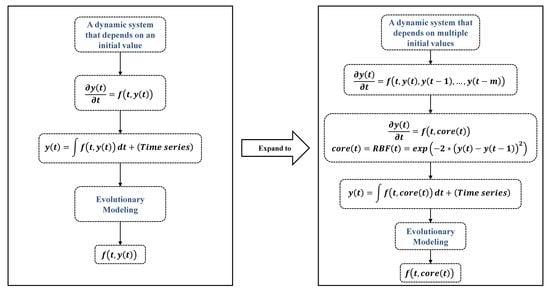
2.2. Backtracking Multiple-Initial-Values Differential Equation

A time series, theoretically, corresponds to a differential scheme for solving an inverse problem. Define an n-dimensional vector $\mathit{A}=({\mathit{a}}_{\mathbf{1}},{\mathit{a}}_{\mathbf{2}},\dots ,{\mathit{a}}_{\mathit{n}})$; its norm is as follows:

$$‖\mathit{A}‖=\sqrt{{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\mathit{a}}_{\mathit{i}}^{\mathbf{2}}}$$

(1)

Suppose a 1D dynamical system ${\mathit{x}}_{\mathit{t}}$, the series of observed values at time: ${\mathit{t}}_{\mathit{i}}={\mathit{t}}_{\mathbf{0}}+\mathit{i}·\Delta \mathit{t},(\mathit{i}=\mathbf{0},\mathbf{1},\dots ,\mathit{j}$), can be described as a column vector form:

$$\mathit{X}=\left(\begin{array}{c}{\mathit{x}}_{{\mathit{t}}_{\mathbf{0}}}\\ {\mathit{x}}_{{\mathit{t}}_{\mathbf{1}}}\\ \dots \\ {\mathit{x}}_{{\mathit{t}}_{\mathit{j}}}\end{array}\right)$$

(2)

where ${\mathit{t}}_{\mathbf{0}}$ is the starting time and $\Delta \mathit{t}$ is the time interval. $\mathit{X}$ satisfies the 1D ordinary differential equation:

$${\mathit{X}}^{\prime }-\mathit{f}\left(\mathit{t},\hspace{1em}\hspace{1em}\mathit{X}\right)=\mathbf{0}$$

(3)

To solve the first-order differential equation $\mathit{f}$:

$${\mathit{x}}_{{\mathit{t}}_{\mathit{n}}}^{\mathrm{*}}={\mathit{f}}^{\prime }\left(\mathit{t},{\mathit{x}}_{{\mathit{t}}_{\mathit{n}-\mathbf{1}}}^{\mathrm{*}}\right)\cdot \Delta \mathit{x}$$

(4)

Then, the 1D dynamic system can be written as

$${\mathit{X}}^{\mathrm{*}}=\left(\begin{array}{c}{\mathit{x}}_{{\mathit{t}}_{\mathbf{0}}}^{\mathrm{*}}\\ {\mathit{x}}_{{\mathit{t}}_{\mathbf{1}}}^{\mathrm{*}}\\ \dots \\ {\mathit{x}}_{{\mathit{t}}_{\mathit{j}}}^{\mathrm{*}}\end{array}\right)$$

(5)

when $‖{\mathit{X}}^{*}-\mathit{X}‖$ is minimized:

$$‖{\mathit{X}}^{\mathrm{*}}-\mathit{X}‖=\sqrt{{\sum }_{\mathit{i}=\mathbf{0}}^{\mathit{j}}{\left({\mathit{x}}_{\mathit{i}}^{\mathrm{*}}-{\mathit{x}}_{\mathit{i}}\right)}^{\mathbf{2}}}$$

(6)

where $\mathit{j}$ is the number of samples for modeling. Once Equation (4) is calculated, lead predictions are performed on the obtained differential equation for $\mathit{\tau }$ steps. For complex and nonlinear systems, it is difficult to reverse-engineer the system by solving ordinary inverse problems, and there are very few predictable solutions. Therefore, this study extends the single initial value inverse problem to backtracking multiple initial values and utilizing more historical information from the time series to improve the efficiency of solving the inverse problem. Equation (4) can be modified as follows:

$${\mathit{x}}_{{\mathit{t}}_{\mathit{n}}}^{\mathrm{*}}={\mathit{f}}^{\prime }\left({\mathit{x}}_{{\mathit{t}}_{\mathit{n}-\mathbf{1}}}^{\mathrm{*}},\mathit{c}\left(\mathit{t}\right)\right)\cdot \Delta \mathit{t}$$

(7)

where $\mathit{c}\left(\mathit{t}\right)=\mathit{c}(\mathit{t},{\mathit{x}}_{{\mathit{t}}_{\mathit{n}-\mathbf{2}}}^{*},\dots ,{\mathit{x}}_{{\mathit{t}}_{\mathit{n}-\mathit{m}}}^{*})$ is the memory kernel function [36], which contains multiple backtracking observations and captures more original information of the system, and m represents the length of the historical backtracking values.

2.3. Evolutionary Algorithm

Evolutionary algorithms in machine learning can simplify complex mathematical problems. The algorithm includes the following steps: input the observational data and preprocess it, set model parameters, initialize the population of differential equations, perform evolutionary operations, calculate the fitness, select the best equations and save them in a seed bank, import seeds for further evolution, and repeat the fitness calculation and equation selection until the stopping criteria are met. Finally, choose the dynamic equation with the best fitness as the predicted equation. The detailed evolutionary algorithm for modeling is referred to He [27]. The evolutionary algorithms for conventional ODE inversion on time series data have been explored, which can help in estimating the parameters of ordinary ODE that govern the underlying dynamics of the complex system. The model can effectively simulate the system’s changes. The process involves selecting the dynamically superior equations as the predictive equations in evolutionary modeling. The historical prediction error of the obtained predictive equations is used to model the error by employing evolutionary modeling again. This allows for the development of an error correction model for the predictive equations. Finally, the predictions from the predictive equations and the error correction model are combined to obtain the final prediction results [51,52].

3. Results

3.1. Local and Global Behaviors in a Complex System

Before conducting mathematical modeling for climate prediction, it is necessary to analyze the theoretical relationship between the global and local behaviors of complex systems. Generally, climate prediction mainly focuses on the changes in precipitation or temperature. However, these variables represent only a small part of complex climate variability and usually reflect the relationship between local and global behaviors. To predict the local behavior of the climate, such as the precipitation, temperature, and sea surface temperature (SST), numerical climate models consider complex physical processes and involve multiple variables by simulating the global dynamics of the climate system to predict variables [53]. According to Takens delay embedding, we can directly perform statistical modeling on a time series. If a time series is generated by a deterministic nonlinear dynamical system, then we can recover and characterize the original dynamic system from that sequence. It can be understood that the statistical modeling of a time series indicates that the local information of the system can reconstruct global features [54,55]. This section first uses the typical nonlinear Lorenz system as an example for verification. The renowned Lorenz system is as follows:

$$\left\{\begin{array}{c}\frac{\mathit{d}\mathit{x}}{\mathit{d}\mathit{t}}=-\mathit{\sigma }\mathit{x}\mathit{+}\mathit{\sigma }\mathit{y}\\ \frac{\mathit{d}\mathit{y}}{\mathit{d}\mathit{t}}=\mathit{\rho }\mathit{x}-\left(\mathit{y}+\mathit{z}\mathit{x}\right)\\ \frac{\mathit{d}\mathit{z}}{\mathit{d}\mathit{t}}=\mathit{x}\mathit{y}-\mathit{\beta }\mathit{z}\end{array}\right.$$

(8)

where $\mathit{\sigma }$, $\mathit{\rho }$, and $\mathit{\beta }$ are system parameters. The values of $\mathit{\sigma }$, $\mathit{\rho }$, and $\mathit{\beta }$ are 10.0, 28.0, and 8/3, which are related to the convective scale, respectively. When $\mathit{\rho }$ > 24.74, the Lorenz system exhibits chaotic behavior. The equation is solved numerically with dt = 0.01, and the Runge–Kutta differencing scheme is used to generate 2000 $\mathit{x}$-components (Figure 1a), which is a high-precision iterative method used to solve nonlinear differential equations [56]. The model training interval is 1–1500 steps, and the validation interval is 1500–2000.

Figure 1 also illustrates the difference between the two types of models. The traditional differential model corresponds to m = 1, where the solution depends only on the initial value ${\mathit{a}}_{\mathbf{0}}$. However, the multi-initial-value model (m > 1) takes into account the system’s memory scale, and the optimal value of m is determined accordingly. In the comparative analysis of inverse problems, three different schemes are considered.

Scheme-A: The classical ODE model of Lorenz-X is inverted using the evolutionary algorithm based on Equation (4). The initial value is not updated, and there is no initial perturbation. The evolutionary program runs for 60 min. Figure 2a shows the simulation results, where the black curve represents Lorenz-X and the blue curve represents the training fit. The fitting correlation coefficient is 0.64 (at the 99% significant level) and the root-mean-square error (RMSE) is 5.90. The prediction correlation coefficient is 0.15 and the RMSE is 8.35. Although the fitting correlation coefficient exceeds 0.60, the fitting error is large and the model fails to reveal the detailed temporal characteristics of the X component. For deterministic systems, the information contained in an observed initial value rapidly decays over time. Without additional information or constraint equations, it is difficult to reconstruct the local details of a complex system. Furthermore, ODE models are sensitive to initial values, which can accelerate error accumulation.

Scheme-B: In climate models, integration is highly sensitive to the initial values, and errors accumulate rapidly over time. To enhance the robustness and reduce error accumulation, a simple and effective scheme involves updating the initial values in a timely manner [57]. In other words, after integrating for a certain period, the latest observed values are used to initialize the initial and boundary conditions. A similar scheme was adopted to improve the sensitivity of the initial values and reduce error accumulation by inserting the latest system information. Specifically, during the evolution training process, the training samples were divided into 30 groups, which meant that, after each training step, 30 initial value updates were performed. Perturbing the initial values helped to improve the robustness of the differential model against disturbances. Similarly, the computational time for training the model was set to 60 min; the modeling results are shown in Figure 2b. The differential model obtained from Scheme-B better captured the details of Lorenz-X. The correlation coefficient increased to 0.789 (at the 95% significant level), and the RMSE decreased to 4.738. The predictive correlation also reached 0.686 (at the 95% significant level) and the RMSE decreased to 6.038. Both the fitting and prediction results approximately revealed the local movement trends of the system, but the errors were still large.

Scheme-C: In this scheme, we constructed the ODE–MKF. As the classical ODE only utilized a single initial value, both Scheme-A and Scheme-B failed to invert to the ideal model and exhibited large errors. This scheme involved MBIV from the current time and constructed an MKF, as shown in Equation (7). The MKF was iteratively updated during the integration processes. The evolution engine solved the inverse problem using Equation (7), with the training samples divided into 50 groups. After training for 60 min, the best model was retained, and the results are shown in Figure 2c. The ODE–MKF almost perfectly approximated the local evolution details of the system. The correlation coefficient increased to 0.971 (at the 99% significance level) and the RMSE decreased to 1.944. The predictive correlation coefficient also reached 0.973 (at the 99% significant level) and the RMSE decreased to 1.924. It is possible to establish separate differential equations and conduct independent predictions of future climatic changes.

In conclusion, the traditional differential model based on a single initial value performed the worst, while the ODE–MKF performed the best. Compared with traditional inversion schemes, the ODE–MKF had a better capability to capture the characteristics of the system and exhibited better robustness. Particularly, it had the capability of multi-step iterative prediction, which allowed for the easy determination of long-term trends in future climatic changes.

3.2. The ODE–MKF Model for Niño3.4

ENSO prediction methods can be broadly categorized into statistical models and dynamic models. In terms of statistical prediction methods, common approaches include canonical correlation analysis, singular spectrum analysis, Markov chains, and others [13,14,15,16,17]. These methods are effective in dealing with linear spatial correlations. However, ENSO is a more complex nonlinear system than the Lorenz system, and it introduces additional uncertainties to the prediction process. In the following analysis, Scheme-C is employed to invert the differential model using the monthly Niño3.4 index instead of Lorenz-X.

The actual dimensions associated with the time step in a differential model are often unknown. When obtaining numerical solutions, the optimal time step can be automatically determined by the evolution algorithm. Figure 3 presents the training results for two different backtracking scales: m = 14 and m = 24. The training interval covers 320 months of SST anomaly data from January 1985 to January 2010. After evolution modeling, the corresponding optimal models were obtained. The black line represents the observed values, the blue line represents the model fitting, and the red line represents the model prediction. When m = 24, the RMSE of the differential model simulation was 0.637 and the correlation coefficient was 0.735 (at a 99% significance level). When m = 14, the RMSE was 0.698 and the correlation coefficient was 0.682 (at the 95% significant level). The model with m = 24 exhibited better fitting than that with m = 14. Both models excellently captured the peak and variations and accurately simulated four representative ENSO events.

ENSO is the most significant source of interannual variability in reflected radiation on a global scale. Thus, the CERES EBAF outgoing longwave radiation flux is engaged in Figure 4 to verify the prediction results. In Figure 4a, the emitted tropical outgoing longwave radiation fluxes are found to closely track changes in the ENSO. The outgoing longwave radiation fluxes tend to increase during the positive ENSO phase and decrease during the negative ENSO phase. Figure 4b further describes the outgoing longwave radiation flux anomalies in December 2015 corresponding to the positive ENSO phase (El Nino), which is consistent with our predicted results. From September 2020 to Spring 2023, a prolonged La Niña event persisted for three years. This period was marked by significant La Niña conditions, as indicated by the anomalies in outgoing longwave radiation fluxes (Figure 4b). These findings highlight the remarkable predictive performance of the ODE–MKF model.

To reduce prediction uncertainties, ensemble methods are commonly employed to improve prediction skill. Figure 5 further shows the ensemble Scheme-C prediction of 27 models with a backtracking scale of m = 24. The ensemble weights of the prediction members were computed from January 2010 to December 2016, spanning 72 months. The verification period for the weighted ensemble prediction was from January 2017 to January 2019, spanning 24 months. Additionally, predictions for the following 24 months (from January 2019 to January 2021) were also provided. The ensemble prediction became smoother, with reduced random fluctuations. Although the ability to predict less significant interannual variations in ENSO was reduced, the ability to capture trends improved. The transition from La Niña to El Niño events during the period from September 2017 to January 2019 was accurately predicted, demonstrating the significant improvement in the ensemble prediction skill. Furthermore, Scheme-C generated a large number of ensemble prediction members by using the initial perturbation method within the same model.

3.3. Influence of the Backtracking Scale

Selecting an appropriate backtracking scale plays a crucial role in improving the prediction accuracy and reducing the modeling time. To estimate the optimal backtracking scale, this section first discusses the optimal SST backtracking scale of the 30 values.

Taking the computational time into account, 30 values ranging from m = 1 to m = 30 were trained for one hour each. The best model was selected from each scenario to compare the differences in the inversion of SST. The results are presented in Figure 6. As the backtracking scale increased, the RMSEs of both model fitting and prediction gradually decreased, while the correlation coefficient increased. This indicates that the precision and robustness of the inverted model improved, and its ability to capture the system characteristics was enhanced. When the backtracking scale reached 24, the RMSE (Figure 6a) slowly decreased and the correlation coefficient (Figure 6b) slightly increased, which suggests the backtracking scale reached a steady state. In other words, the memory length of SST reached 24 months, and the memory information carried by observations further in the past may have decayed.

To investigate the contributions of different initial values, the backtracking scale was allowed to vary between 1 and 35, and 2000 models were inverted. Among them, 211 differential models met both the fitting and prediction criteria. Figure 7 presents the usage distribution of the initial values. The 35 initial values were used 1376 times. The most effective initial values for reconstructing the system variations were concentrated from the 4th to 6th time steps, with the usage frequency exceeding 59 times before the current observation, as well as the 14th and 22nd–25th time steps. The usage frequency for the backtracking scale ranges from 26 to 35 was relatively low, indicating that the memory had decayed. In addition, the latest initial value was not the most frequently used, although the usage frequency surpassed the average (by 52 times). This reveals that the information of the original system was not necessarily stored in the most recent observation, and the system characteristics could be better reconstructed by utilizing multiple observations, which is similar to the concept of embedding theory and aims to map low-dimensional information back to a high-dimensional space [57].

ENSO is characterized by the periodic fluctuation in SST and atmospheric pressure patterns called Southern Oscillation (SO) [38]. Ocean processes are generally slow, with a longer memory. However, atmospheric patterns usually change quickly with noisy processes. Thus, this section also discusses the self-memory scale of the atmosphere using SOI.

In Figure 8, when the backtracking scale was m = 12, the best training model had a RMSE of fitting of 0.71, and the correlation coefficient was 0.68 (at the 99% significance level). The RMSE of the prediction model was 0.75 and the correlation coefficient was 0.628 (at the 99% significance level). Compared with Niño3.4, the inversion of the SO was more challenging, with higher demands for initial values and a shorter timespan for perturbing the initial values. Consequently, the predictive skill of the model was also decreased. Although the differential model captured the overall trend of the SO, it failed to reflect its variations. The same problem exists in past methods used for predicting SOI like the maximum entropy method (MEM), which is sensitive to the overall trend [58]. It is evident that the fast-changing atmospheric motion in the climate system is subject to a higher level of stochastic forcing, leading to substantial noise in SO prediction. More important is the fact that the ODE–MKF model forecast combination has some predictive capability that can be used for predicting the phase and amplitude of ENSO up to 1 year in advance [59]. In addition, forecasting based on prefiltered SOI time series through PCA rather than on the raw SOI itself should be recommended in the future [60].

4. Discussions

Traditional climate prediction methods are primarily based on mathematical and statistical techniques applied to time series data [6,8]. These methods offer simplicity, convenience, and low computational costs, along with a wide range of available approaches. However, these methods mainly follow the additive modeling approach, are primarily suited for linear and stationary data, and often lack the ability to handle nonlinear processes [29]. The optimal distribution of the retrospective scale was closely related to the memory inertia of the system. For Niño3.4, the optimal value exceeded 24 months (Figure 9a). The ODE–MKF time series forecasting modeling approach proposed offers a combination of numerical modeling features and statistical techniques, taking advantage of the strengths of both numerical modeling and statistical methods and capturing the long-term dependencies and characteristics of complex and nonlinear systems (Figure 9b). We find that trained variations in ENSO correspond to the main modes of variability of weather and climate and variations in CERES EBAF radiation flux anomalies [52]. Additionally, it benefitted from the simplicity and ease of use of time series methods, resulting in low computational costs and convenient model development. Through machine learning techniques, the ODE–MKF model enabled the utilization of historical evolution information and compensated for the spatial information deficiency by leveraging the information available at different time scales. Though the overall trends of predictions perform well, peaks do not. In Figure 3b, peaks from the model prediction around 2016 and 2019 are close; however, there is a large gap from the observation, which means the ODE–MKF model still needs improving accuracy on peaks. Traditional statistical methods often employ filtering techniques to remove noise and retain the main components for modeling and prediction [61], which can be used to improve the prediction on systems with substantial noise like SO. Mokhov and Smirnov [62] used an approach that filtered out variations unrelated to the SO and separated the high-frequency variability from the low-frequency variability associated with El Niño cycles. For highly noisy time series data, such as SO, preprocessing techniques such as filtering can be used in combination with ODE–MKF to improve the prediction accuracy.

In general, the variance of the ODE–MKF prediction error can be reduced by an error-minimizing forecast and climate model simulation combination, which further improves the correlation skill [59]. The nonlinear combination and machine learning achieve the largest profit of ENSO. Additionally, the complex ocean–atmosphere interactions involved in the evolution of ENSO pose a challenge for the GCMs prediction. Furthermore, the interannual and interdecadal variabilities of ENSO strengthen its related atmospheric and oceanic processes, leading to a stronger response of SST, which further increased the difficulty in prediction [63,64]. Thus, further research is possible, using this approach to compensate for the limitations of ODE–MKF in considering dynamic processes. Further, the combination of the two approaches assimilated in climate model prediction could lead to more insights into climate change.

5. Conclusions

This study adopted a combined approach of data-driven and physical processes, leveraging the intelligent advantages of machine learning to automatically determine the memory kernel function during differential modeling. The kernel function expanded the integration problem of a single initial value into a differential equation that embedded multiple initial values. It played a central role in the differential equation, connecting the past and the present, and reflected the inherent properties of the dynamic system. It enhanced the descriptive capability of complex nonlinear systems.

This study first conducted experiments using the Lorenz system to demonstrate that the proposed modeling approach could accurately simulate and predict the local processes of complex systems. Then, taking the ENSO system as an example, the Niño3.4 and SO indices were modeled separately, verifying the capability of the approach to handle complex nonlinear data. The developed differential models exhibited good robustness. Based on the memory inertia of the complex system, they achieved 6-month and 24-month advance predictions with satisfactory results (Figure 9). Additionally, the optimal distribution of the retrospective scale was closely related to the memory inertia of the system. For Niño3.4, the optimal value exceeded 24 months (Figure 9a). However, the SO index was influenced by seasonal high-frequency variations and was subject to more random noise, which resulted in less persistence of memory compared with Niño3.4. and this led to prediction errors of the SO index by the model. The tested values of the retrospective scale in this study were less than 1 year, and the effective prediction length reached 6 months.