Dynamical Response of Particles in Asymmetric Ratchet Potential
Abstract
:1. Introduction
2. The Inertia Ratchet
3. Results and Discussion
3.1. Approximation Technique
3.2. Analysis with the Method of Multiple Scales
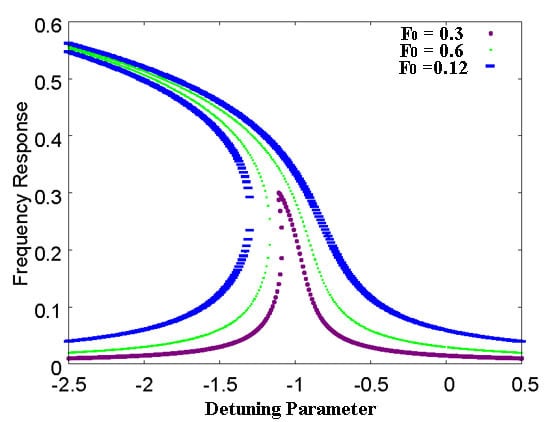
3.3. Principal Resonance
3.4. Stability of the Steady-State Solution
4. Conclusions
Author Contributions
Conflicts of Interest
Appendix
Acknowledgments
References
- Hanggi, P.; Marchesoni, F. Artificial Brownian transport on the nanoscale. Rev. Mod. Phys 2009, 81, 387–442. [Google Scholar]
- Julicher, F.; Ajdari, A.; Prost, J. Modelling molecular motors. Rev. Mod. Phys 1997, 69, 1269–1281. [Google Scholar]
- Marchesoni, F.; Savel’ev, S.; Nori, F. Achieving optimal rectification using underdamped rocked ratchets. Phys. Rev. E 2006, 73. [Google Scholar] [CrossRef]
- Astumian, R.D. Thermodynamics and kinetics of a Brownian motor. Science 1997, 276, 917–922. [Google Scholar]
- Reimann, P. Brownian Motors: Noisy Transport Far from Equilibrium. Phys. Rep 2002, 361, 57–265. [Google Scholar]
- Jung, J.; Kissner, J.G.; Hanggi, P. Regular and chaotic transport in asymmetric periodic potentials: Inertia ratchets. Phys. Rev. Lett 1996. [Google Scholar]
- Mateos, J.L. Chaotic transport and current reversal in deterministic ratchets. Phys. Rev. Lett 2000. [Google Scholar]
- Son, W.S.; Kim, I.; Park, Y.J.; Kim, C.M. Current reversal with type-I intermittency in deterministic inertia ratchets. Phys. Rev. E 2003, 68. [Google Scholar] [CrossRef]
- Barbi, M.; Salerno, M. Phase locking effect and current reversals in deterministic under-damped ratchets. Phys. Rev. E 2000. [Google Scholar]
- Kenfack, A.; Sweetnam, S.M.; Pattanayak, A.K. Bifurcations and sudden current change in ensembles of classically chaotic ratchets. Phys. Rev. E 2007, 75. [Google Scholar] [CrossRef]
- Mateos, J.L. Current reversals in deterministic chaotic ratchets. Phys. D 2002, 168–169, 205–219. [Google Scholar]
- Mateos, J.L. Current reversals in chaotic ratchets: The battle of attractors. Phys. A 2004, 325, 92–100. [Google Scholar]
- Mateos, J.L. Intermittency and deterministic diffusion in chaotic ratchets. Commun. Nonlinear Sci. Numer. Simul 2003, 8, 253–263. [Google Scholar]
- Vincent, U.E.; Njah, A.N.; Akinlade, O.; Solarin, A.R.T. Phase synchronization in unidirectionally coupled chaotic ratchets. Chaos 2004, 14, 1018–1025. [Google Scholar]
- Vincent, U.E.; Kenfack, A.; Njah, A.N.; Akinlade, O. Bifurcation and chaos in coupled ratchets exhibiting synchronized dynamics. Phys. Rev. E 2005, 72. [Google Scholar] [CrossRef]
- Kostur, M.; Hanggi, P.; Talkner, P.; Meteos, J.L. Anticipated synchronization in coupled inertia ratchets with time-delay feedback. Phys. Rev. E 2005, 72. [Google Scholar] [CrossRef]
- Vincent, U.E.; Laoye, J.A. Synchronization and control of directed trasnport in chaotic ratchets via active control. Phys. Lett. A 2007, 363, 91–95. [Google Scholar]
- Guo, L.X.; Hu, M.F.; Xu, Z.Y. Impulsive synchronization and control of directed transport in chaotic ratchets. Chin. Phys. B 2010, 19. [Google Scholar] [CrossRef]
- Lu, P.L.; Yang, Y.; Huang, L. Synchronization of linearly coupled networks of deterministic ratchets. Phys. Lett. A 2008, 372, 3978–3985. [Google Scholar]
- Zarlenga, D.G.; Larrondo, H.A.; Arizmendi, C.M.; Family, F. Complex synchronization structure of an overdamped ratchet with discontinuous periodic forcing. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef]
- Xu, S.Y.; Yang, Y.; Song, L. Control-oriented approaches to anticipating synchronization of chaotic deterministic ratchets. Phys. Lett. A 2009, 373, 2226–2236. [Google Scholar]
- Sengupta, S.; Guantes, R.; Miret-Artes, S.; Hanggi, P. Controlling directed transport in two-dimensional periodic structures under crossed electric fields. Phys. A 2004, 338, 406–416. [Google Scholar]
- Vincent, U.E.; Kenfack, A.; Senthilkumar, D.V.; Mayer, D.; Kurths, J. Current reversals and synchronization in coupled ratchets. Phys. Rev. E 2010, 82. [Google Scholar] [CrossRef]
- Nana-Nbendjo, B.R.; Vincent, U.E.; McClintock, P.V.E. Multi-resonance and enhanced synchronization in stochastically coupled chaotic ratchets. Int. J. Bifurcat. Chaos 2012, 22. [Google Scholar] [CrossRef] [Green Version]
- Vincent, U.E.; Nana-Nbendjo, B.R.; McClintock, P.V.E. Collective dynamics of a network of ratchets coupled via a stochastic dynamical environment. Phys. Rev. E 2013, 87. [Google Scholar] [CrossRef]
- Borromeo, M.; Costantini, G.; Marchesoni, F. Deterministic ratchets: Route to diffusive transport. Phys. Rev. E 2002, 65. [Google Scholar] [CrossRef]
- Arizmendi, C.M.; Family, F.; Salas-Brito, A.L. Quenched disorder effects on deterministic inertia ratchets. Phys. Rev. E 2001, 63. [Google Scholar] [CrossRef]
- Luchinsky, D.G.; Greenall, M.J.; McClintock, P.V.E. Resonant rectification of fluctuations in a Brownian ratchet. Phys. Lett. A 2000, 273, 316–321. [Google Scholar] [Green Version]
- Nayfeh, A.H. Perturbation Methods; Wiley and Sons: New York, NY, USA, 1973. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley and Sons: New York, NY, USA, 1979. [Google Scholar]
- Huberman, B.A.; Cructhfield, J.P.; Packard, N.H. Noise phenomena in Josephson junctions. Appl. Phys. Lett 1980. [Google Scholar]
- Lu, P.; Wu, Q.; Yang, Y. Controlling transport and synchronization in non-identical inertial ratchets. J. Optim. Theory Appl 2013, 157, 888–899. [Google Scholar]






© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marte, U.A.; Vincent, U.E.; Njah, A.N.; Badmus, B.S. Dynamical Response of Particles in Asymmetric Ratchet Potential. Symmetry 2014, 6, 896-908. https://0-doi-org.brum.beds.ac.uk/10.3390/sym6040896
Marte UA, Vincent UE, Njah AN, Badmus BS. Dynamical Response of Particles in Asymmetric Ratchet Potential. Symmetry. 2014; 6(4):896-908. https://0-doi-org.brum.beds.ac.uk/10.3390/sym6040896
Chicago/Turabian StyleMarte, Usman A., Uchechukwu E. Vincent, Abdulahi N. Njah, and Biodun S. Badmus. 2014. "Dynamical Response of Particles in Asymmetric Ratchet Potential" Symmetry 6, no. 4: 896-908. https://0-doi-org.brum.beds.ac.uk/10.3390/sym6040896