On the Performances of Trend and Change-Point Detection Methods for Remote Sensing Data
Abstract
:1. Introduction
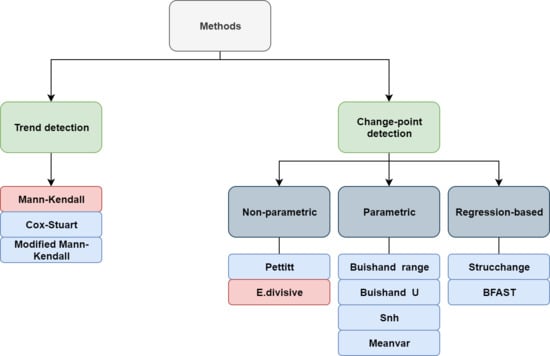
2. Trend and Change-Point Detection
2.1. Trend Detection Methods
2.1.1. Mann–Kendall
2.1.2. Cox–Stuart
2.2. Change-Point Detection Methods
2.2.1. Pettitt’s Test
2.2.2. Buishand Tests
2.2.3. Standard Normal Homogeneity Test (Snh)
2.2.4. Identifying Changes Using Both Mean and Variance Jointly (Meanvar)
2.2.5. Structure Change (Strucchange)
2.2.6. Breaks for Additive Seasonal and Trend (BFAST)
2.2.7. Hierarchical Divisive (E.divisive)
2.3. Trend versus Change-Point
3. Simulation Study
- The empirical power of the test is calculated in the cloud where artificial changes are produced, and it is given by dividing the number of detected trend/change-points inside the cloud by the total number of pixels of the cloud. The power of the test is a good indicator with which to reveal how well the methods detect the existence of the produced abrupt change within the cloud.
- The type I error probability is the probability of introducing a false trend/change-point (a false positive). This is estimated by dividing the number of detected change-points outside the cloud by the total number of pixels outside the cloud.
- The mean absolute error (MAE) checks how accurately the methods detect the artificial change-points. This is only calculated for methods that are designed to detect change-points. Assuming a true change-point is placed at time-period k, , the MAE is of the formwhere is the estimated change-point for the j-th pixel of the cloud in the i-th multi-layer raster. Note that 100 is the number of simulated multi-layer rasters, and 13 is the number of pixels falling in the randomly located cloud.
3.1. Computational Details
3.2. Scenario 1: Normally Distributed Remote Sensing Data
3.3. Scenario 2: Autoregressive Remote Sensing Data
3.4. Summary
4. Remote Sensing LST Data of Navarre, Spain
Results
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| bcpw | Mann-Kendall bias corrected pre-whitening approach of Hamed [34]. |
| BFAST | breaks for additive season and trend. |
| E.divisive | hierarchical divisive. |
| MAE | mean absolute error. |
| Meanvar | Identifying changes using both mean and variance. |
| mmkh | Mann–Kendall variance corrected approach of Hamed and Rao [30]. |
| mmkh3 | Mann–Kendall variance corrected approach of Hamed and Rao [30] by considering only the first three lags. |
| mmky | Mann–Kendall variance corrected approach of Yue and Wang [33]. |
| mmky1 | Mann–Kendall variance corrected approach of Yue and Wang [33] by considering only the first lag. |
| MODIS | Moderate Resolution Imaging Spectroradiometer. |
| LST | land surface temperature. |
| pwmk | Mann–Kendall pre-whitening approach of Von Storch [31]. |
| Snh | standard normal homogeneity. |
| Strucchange | structure change. |
| TIR | thermal infrared. |
| tfpwmk | Mann–Kendall trend-free pre-whitening approach of Yue et al. [32]. |
| UTM | universal transverse mercator. |
References
- Montanez, G.D.; Amizadeh, S.; Laptev, N. Inertial hidden markov models: Modeling change in multivariate time series. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef] [Green Version]
- Sharma, S.; Swayne, D.A.; Obimbo, C. Trend analysis and change point techniques: A survey. Energy Ecol. Environ. 2016, 1, 123–130. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.M.; Cabello, D.; Tomás-Burguera, M.; Martín-Hernández, N.; Beguería, S.; Azorin-Molina, C.; Kenawy, A.E. Drought variability and land degradation in semiarid regions: Assessment using remote sensing data and drought indices (1982–2011). Remote Sens. 2015, 7, 4391–4423. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Huang, X.; Zhang, Y.; Yu, D. Long-term changes in water clarity in Lake Liangzi determined by remote sensing. Remote Sens. 2018, 10, 1441. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Huang, X.; Liang, H.; Sun, Y.; Feng, Q.; Liang, T. Tracking snow variations in the Northern Hemisphere using multi-source remote sensing data (2000–2015). Remote Sens. 2018, 10, 136. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Lu, L.; Weng, Q.; Xie, Y.; Guo, H. Monitoring urban dynamics in the southeast USA using time-series DMSP/OLS nightlight imagery. Remote Sens. 2016, 8, 578. [Google Scholar] [CrossRef] [Green Version]
- NourEldeen, N.; Mao, K.; Yuan, Z.; Shen, X.; Xu, T.; Qin, Z. Analysis of the spatiotemporal change in Land Surface Temperature for a long-term sequence in Africa (2003–2017). Remote Sens. 2020, 12, 488. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Yu, S. Spatiotemporal variability of land surface phenology in China from 2001–2014. Remote Sens. 2017, 9, 65. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Jia, K.; Liang, S.; Liu, M.; Wei, X.; Yao, Y.; Zhang, X.; Liu, D. Spatio-temporal analysis and uncertainty of fractional vegetation cover change over northern China during 2001–2012 based on multiple vegetation data sets. Remote Sens. 2018, 10, 549. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Jin, L.; Wang, H. Vegetation changes along the Qinghai-Tibet Plateau engineering corridor since 2000 induced by climate change and human activities. Remote Sens. 2018, 10, 95. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Pollution trends in China from 2000 to 2017: A multi-sensor view from space. Remote Sens. 2020, 12, 208. [Google Scholar] [CrossRef] [Green Version]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: Oxford, UK, 1948. [Google Scholar]
- Cox, D.R.; Stuart, A. Some quick sign tests for trend in location and dispersion. Biometrika 1955, 42, 80–95. [Google Scholar] [CrossRef] [Green Version]
- Pettitt, A. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Matteson, D.S.; James, N.A. A nonparametric approach for multiple change point analysis of multivariate data. J. Am. Stat. Assoc. 2014, 109, 334–345. [Google Scholar] [CrossRef] [Green Version]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Buishand, T.A. Tests for detecting a shift in the mean of hydrological time series. J. Hydrol. 1984, 73, 51–69. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Hinkley, D.V. Inference about the change-point in a sequence of random variables. Biometrika 1970, 57, 1–17. [Google Scholar] [CrossRef]
- Horváth, L. The maximum likelihood method for testing changes in the parameters of normal observations. Ann. Stat. 1993, 21, 671–680. [Google Scholar] [CrossRef]
- Picard, F.; Robin, S.; Lavielle, M.; Vaisse, C.; Daudin, J.J. A statistical approach for array CGH data analysis. BMC Bioinf. 2005, 6, 27. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Killick, R.; Eckley, I. changepoint: An R package for changepoint analysis. J. Stat. Softw. 2014, 58, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Zeileis, A.; Leisch, F.; Hornik, K.; Kleiber, C. strucchange: An R package for testing for structural change in linear regression models. J. Stat. Softw. 2002, 7, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Zeileis, A.; Kleiber, C.; Krämer, W.; Hornik, K. Testing and dating of structural changes in practice. Comput. Stat. Data Anal. 2003, 44, 109–123. [Google Scholar] [CrossRef] [Green Version]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Verstraeten, G.; Poesen, J.; Demarée, G.; Salles, C. Long-term (105 years) variability in rain erosivity as derived from 10-min rainfall depth data for Ukkel (Brussels, Belgium): Implications for assessing soil erosion rates. J. Geophys. Res. Atmos. 2006, 111, D22. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef] [Green Version]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of statistical analysis in climate research. In Analysis of Climate Variability: Applications of Statistical Techniques; von Storch, H., Navarra, A., Eds.; Springer Science & Business Media: Berlin, Germany, 1999; pp. 11–26. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Hamed, K. Enhancing the effectiveness of prewhitening in trend analysis of hydrologic data. J. Hydrol. 2009, 368, 143–155. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. The importance of prewhitening in change point analysis under persistence. Stoch. Environ. Res. Risk Assess. 2016, 30, 763–777. [Google Scholar] [CrossRef] [Green Version]
- MODIS. Moderate Resolution Imaging Spectroradiometer. Available online: https://modis.gsfc.nasa.gov/ (accessed on 1 February 2020).
- Chen, J.; Gupta, A.K. Parametric Statistical Change Point Analysis: With Applications to Genetics, Medicine, and Finance; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Van Belle, G.; Hughes, J.P. Nonparametric tests for trend in water quality. Water Resour. Res. 1984, 20, 127–136. [Google Scholar] [CrossRef]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Lettenmaier, D.P. Multivariate nonparametric tests for trend in water quality. J. Am. Water Resour. Assoc. 1988, 24, 505–512. [Google Scholar] [CrossRef]
- Libiseller, C.; Grimvall, A. Performance of partial Mann–Kendall tests for trend detection in the presence of covariates. Env. Off. J. Int. Env. Soc. 2002, 13, 71–84. [Google Scholar] [CrossRef]
- KuLKARNI, A.; von Storch, H. Monte Carlo experiments on the effect of serial correlation on the Mann-Kendall test of trend. Meteorol. Z. 1995, 4, 82–85. [Google Scholar] [CrossRef]
- Jen, T.; Gupta, A.K. On testing homogeneity of variances for Gaussian models. J. Stat. Comput. Simul. 1987, 27, 155–173. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Zeileis, A. A unified approach to structural change tests based on ML scores, F statistics, and OLS residuals. Econom. Rev. 2005, 24, 445–466. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-PLUS; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Szekely, G.J.; Rizzo, M.L. Hierarchical clustering via joint between-within distances: Extending Ward’s minimum variance method. J. Classif. 2005, 22, 151–183. [Google Scholar] [CrossRef]
- Rizzo, M.L.; Székely, G.J. Disco analysis: A nonparametric extension of analysis of variance. Ann. Appl. Stat. 2010, 4, 1034–1055. [Google Scholar] [CrossRef] [Green Version]
- James, N.A.; Matteson, D.S. ecp: An R package for nonparametric multiple change point analysis of multivariate data. J. Stat. Softw. 2015, 62, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Hijmans, R.J. raster: Geographic Data Analysis and Modeling, R Package Version 3.0-12; 2020. Available online: https://cran.r-project.org/web/packages/raster/index.html (accessed on 6 March 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Pohlert, T. trend: Non-Parametric Trend Tests and Change-Point Detection, R package version 1.1.2; 2020. Available online: https://cran.r-project.org/web/packages/trend/index.html (accessed on 6 March 2020).
- Patakamuri, S.K.; O’Brien, N. modifiedmk: Modified Versions of Mann Kendall and Spearman’s Rho Trend Tests, R package version 1.5.0; 2020. Available online: https://cran.r-project.org/web/packages/modifiedmk/index.html (accessed on 6 March 2020).
- Killick, R.; Haynes, K.; Eckley, I. changepoint: An R Package for Changepoint Analysis, R package version 2.2.2; 2016. Available online: https://cran.r-project.org/web/packages/changepoint/index.html (accessed on 6 March 2020).
- Pebesma, E.; Bivand, R. Classes and methods for spatial data in R. R News 2005, 5, 9–13. [Google Scholar]
- Bivand, R.; Pebesma, E.; Gomez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer-Verlag: New York, NY, USA, 2016. [Google Scholar]
- Appelhans, T.; Detsch, F.; Reudenbach, C.; Woellauer, S. mapview: Interactive Viewing of Spatial Data in R, R package version 2.7.0; 2019. Available online: https://cran.r-project.org/web/packages/mapview/index.html (accessed on 6 March 2020).
- Benali, A.; Carvalho, A.; Nunes, J.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Pérez-Goya, U.; Montesino-SanMartin, M.; Militino, A.F.; Ugarte, M.D. RGISTools: Handling Multiplatform Satellite Images, R package version 0.9.7; 2019. Available online: https://cran.r-project.org/web/packages/RGISTools/index.html (accessed on 6 March 2020).
- Detsch, F. gimms: Download and Process GIMMS NDVI3g Data, R package version 1.1.3; 2020. Available online: https://cran.r-project.org/web/packages/gimms/index.html (accessed on 6 March 2020).
- Appelhans, T.; Detsch, F.; Nauss, T. remote: Empirical orthogonal teleconnections in R. J. Stat. Softw. 2015, 65, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Cleveland, W.S.; Grosse, E.; Shyu, W.M. Local regression models. In Statistical Models in S; Hastie, T., Ed.; Routledge: Abingdon, Oxfordshire, UK, 2017; pp. 309–376. [Google Scholar]
- Kifer, D.; Ben-David, S.; Gehrke, J. Detecting change in data streams. In Proceedings of the Thirtieth International Conference on Very Large Data Bases VLDB Endowment, Toronto, ON, Canada, 31 August–3 September 2004; Volume 30, pp. 180–191. [Google Scholar]















| R Package | Method | Function |
|---|---|---|
| trend (version 1.1.2) | Mann–Kendall | mk.test |
| Multivariate Mann–Kendall | mult.mk.test | |
| Cox–Stuart | cs.test | |
| Pettitt | pettitt.test | |
| Buishand Range | br.test | |
| Buishand U | bu.test | |
| Snh | snh.test | |
| modifiedmk (version 1.5.0) | Hamed bias corrected pre-whitening | bcpw |
| Yue and Wang variance correction | mmky | |
| mmky1lag | ||
| Hamed and Rao variance correction | mmkh | |
| mmkh3lag | ||
| von Storch pre-whitening | pwmk | |
| Yue et al. trend-free pre-whitening | tfpwmk | |
| changepoint (version 2.2.2) | Meanvar | cpt.meanvar |
| strucchange (version 1.5-2) | Strucchange | breakpoints |
| bfast (version 1.5.7) | BFAST | bfast |
| ecp (version 3.1.2) | E.divisive | e.divisive |
| Method | Proportion | Method | Proportion |
|---|---|---|---|
| Buishand Range | 0.0501 | Buishand U | 0.0510 |
| Snh | 0.0487 | Pettitt | 0.0398 |
| Univariate E.divisive | 0.0506 | Strucchange | 0.0244 |
| Meanvar | 0.0854 | BFAST | 0.0050 |
| Univariate Mann–Kendall | 0.0521 | Cox–Stuart | 0.0441 |
| mmkh | 0.0912 | mmkh3 | 0.0575 |
| mmky | 0.4837 | mmky1 | 0.0559 |
| bcpw | 0.0528 | pwmk | 0.0507 |
| tfpwmk | 0.0527 | ||
| Multivariate E.divisive | 0.0600 | Multivariate Mann–Kendall | 0.0300 |
| Method | Proportion | Method | Proportion |
|---|---|---|---|
| Buishand Range | 0.9828 | Buishand U | 0.8284 |
| Snh | 0.9421 | Pettitt | 0.8829 |
| Univariate E.divisive | 0.9894 | Strucchange | 0.9595 |
| Meanvar | 0.9615 | BFAST | 0.9635 |
| Univariate Mann–Kendall | 0.5027 | Cox–Stuart | 0.4301 |
| mmkh | 0.2453 | mmkh3 | 0.1583 |
| mmky | 0.5166 | mmky1 | 0.0685 |
| bcpw | 0.0602 | pwmk | 0.0538 |
| tfpwmk | 0.6730 | ||
| Multivariate E.divisive | 1.0000 | Multivariate Mann–Kendall | 0.5100 |
| Data | Season | CV | Min | 1st Q. | Med | 3rd Q. | Max |
|---|---|---|---|---|---|---|---|
| LST day | Jan - Mar | 0.017 | 264.4 | 280.4 | 283.1 | 287.1 | 300.6 |
| Apr - Jun | 0.018 | 271.8 | 293.3 | 296.2 | 300.4 | 313.4 | |
| Jul - Sep | 0.018 | 283.9 | 297.5 | 301.1 | 306.2 | 315.6 | |
| Oct - Dec | 0.019 | 264.9 | 281.2 | 284.4 | 288.9 | 302.2 | |
| LST night | Jan - Mar | 0.010 | 259.2 | 273.4 | 274.9 | 276.8 | 284.1 |
| Apr - Jun | 0.013 | 266.5 | 280.4 | 282.9 | 285.8 | 295.7 | |
| Jul - Sep | 0.010 | 272.9 | 285.5 | 287.5 | 289.6 | 296.2 | |
| Oct - Dec | 0.013 | 262.4 | 275.1 | 277.2 | 280.2 | 290.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Militino, A.F.; Moradi, M.; Ugarte, M.D. On the Performances of Trend and Change-Point Detection Methods for Remote Sensing Data. Remote Sens. 2020, 12, 1008. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12061008
Militino AF, Moradi M, Ugarte MD. On the Performances of Trend and Change-Point Detection Methods for Remote Sensing Data. Remote Sensing. 2020; 12(6):1008. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12061008
Chicago/Turabian StyleMilitino, Ana F., Mehdi Moradi, and M. Dolores Ugarte. 2020. "On the Performances of Trend and Change-Point Detection Methods for Remote Sensing Data" Remote Sensing 12, no. 6: 1008. https://0-doi-org.brum.beds.ac.uk/10.3390/rs12061008